基于裂纹扩展脆性岩石动力压缩力学特性研究*

李晓照，戚承志

（1. 北京建筑大学土木与交通工程学院，北京 100044；2. 北京未来城市设计高精尖创新中心，北京 100044）

动力压缩荷载作用脆性岩石力学特性的研究，对于深部地下工程围岩受到地震、冲击及爆炸荷载作用下的稳定性分析有着重要的意义。关于应变率对岩石力学特性影响的研究，对于岩石动态力学性能分析有着重要价值。众多学者，通过开展霍布金森杆动力试验，研究了不同应变率下岩石的应力-应变本构曲线、岩石动态强度、动态破坏形态等特性[1-4]。也有学者研究了在恒定轴压与围压作用下，岩石承受循环重复冲击荷载作用下的力学性能[5-7]。

在这些试验研究的基础上，许多理论模型被提出。曹文贵等[8]通过将非线性动态强度准则与统计损伤理论相结合，建立岩石动态统计损伤本构模型，并根据试验结果确定模型参数，计算分析了高应变对岩石动态本构关系的影响。李夕兵等[9-10]将统计损伤模型和黏弹性模型相结合，提出了中应变率作用下岩石动载本构模型，并分析了重复冲击荷载作用下岩石的动力特性。谢理想等[11]基于岩石动态强度理论模型、连续损伤理论及Bingham 模型，蔡灿等[12]基于Maxwell 模型、Bingham 模型及孔隙度损伤模型分别建立了不同组合模型，研究了岩石应变率相关的应力应变本构关系。戚承志等[13-14]基于热活化机制与宏观黏性机制，研究了应变率与岩石强度之间关系，并分析了动态荷载作用下岩石破坏块度分布物理机理。赵坚等[15]、马林建等[16]基于动态试验结果并结合摩尔库伦及霍克布朗强度准则，提出了应变率相关的动态强度准则。宫凤强等[17]基于岩石从低到高应变率范围内的率效应试验结果，建立了一种基于率效应动态增强因子统一模型，探讨了应变率对压缩强度、切线模量和峰值应变的影响。以上均是通过宏观现象研究了岩石动态变化特性，无法解释动态荷载作用下，岩石内部细观裂纹机理变化特性。

岑夺丰等[18]通过细观颗粒平行黏结模型的模拟，研究了高应变率压缩作用，单裂隙岩样的损伤演化及细观位移场，结果表明不同高应变率对岩样最终破裂形态影响不大，但随应变率的增大，细观裂纹越多且局部化程度越强。潘红宇等[19]通过用数字图像处理技术，分析了不同应变率下单轴压缩下岩石表面裂隙扩展下的应变场变化特征，然而该研究只是分析准静态压缩荷载作用下的裂纹特性，没有研究动态荷载下岩石裂纹扩展特性。刘红岩等[20]将基于岩石动态损伤TCK 模型与基于断裂损伤理论推出的节理岩体损伤本构模型相结合，提出了一个考虑裂纹节理几何特性的岩体动态损伤本构模型。

然而对能够建立脆性岩石内部细观动态裂纹扩展与宏观动态应力-应变本构关系的理论模型研究较少。本文中，将准静态压缩荷载作用下裂纹扩展诱发的应力应变本构关系模型、基于裂纹与应变关系得到的裂纹速率与应变率关系及裂纹速率与断裂韧度关系相结合，提出了一个基于细观裂纹扩展作用下的动态应力应变本构关系模型，并讨论岩石应变率、初始损伤、围压及模型参数对应力应变关系曲线的影响。

1 理论模型

1.1 准静态裂纹扩展应力-应变关系

本文中提出了一个动态压缩荷载作用下，基于岩石内部裂纹扩展诱发的应力-应变本构关系模型（见图1），模型中各项参数详见下面关于模型理论公式的叙述。该模型是由准静态作用下裂纹扩展模型，与动态裂纹扩展与准静态裂纹扩展关系，及新建立的裂纹扩展速率与应变率关系相结合而提出的。在该模型中，当不考虑动态裂纹扩展作用时，模型内部准静态裂纹扩展与承受应力状态（轴向应力σ1、围压σ3）之间的关系可以表示为[21]：

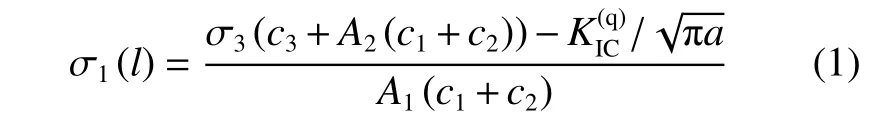
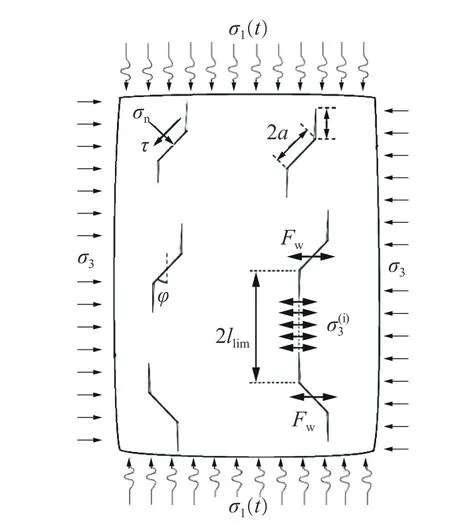
图 1 动态压缩荷载作用下的裂纹扩展模型Fig. 1 Crack growth model under dynamic compressive loadings

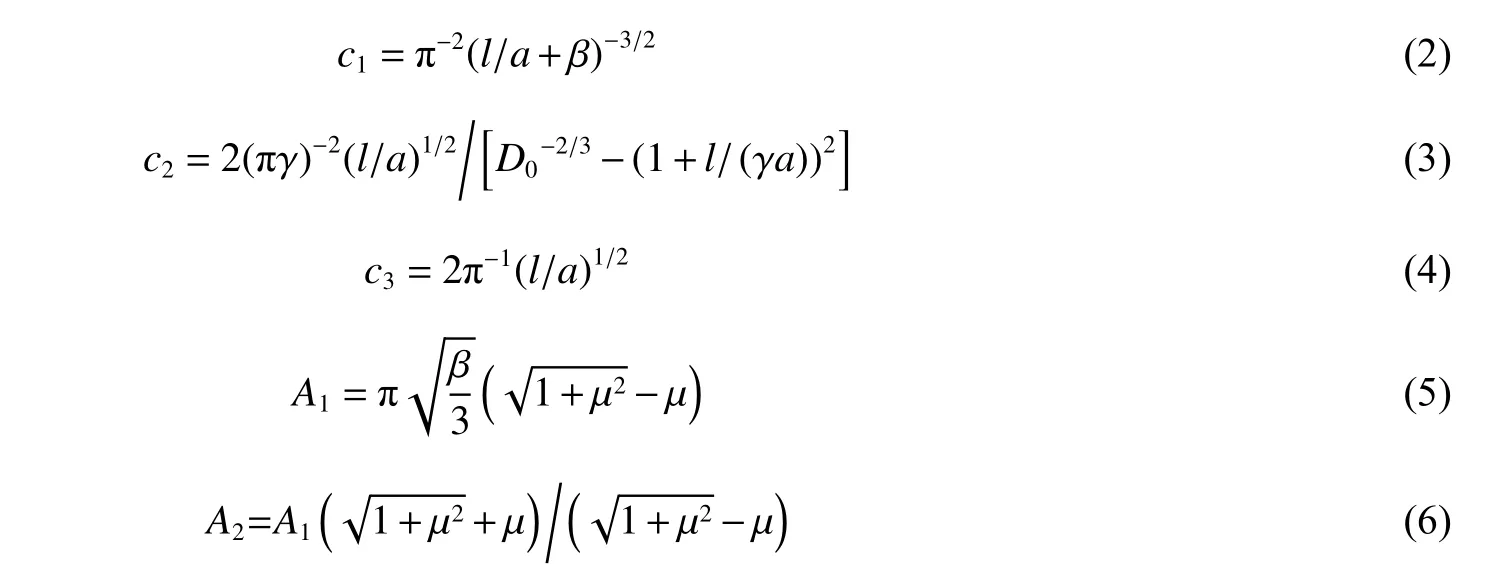
此外，低围压脆性岩石宏观轴向应变ε1与细观裂纹扩展长度l 间的关系可表示为[22]：

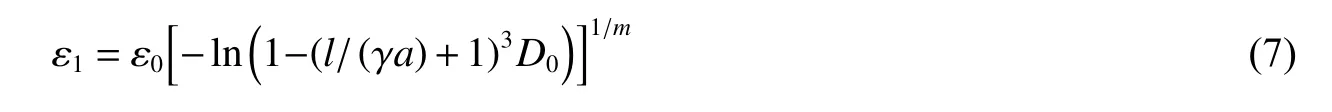
式中：m、ε0分别为材料常数。

将式(7)代入式(1)，裂纹扩展下（即l＞0），岩石准静态应力-应变本构关系可表示为[22]：

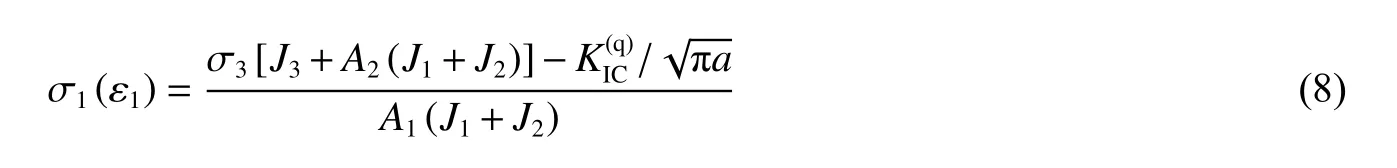
式中：

此外，当裂纹长度l=0 时，基于式（1）和（7），岩石轴向起裂应力σ1c和裂纹起裂应变ε1c可以分别表示为：

假设岩石内部裂纹扩展前（即0＜ ε1＜ε1c），岩石服从线弹性变形，则应力-应变关系可表示为：

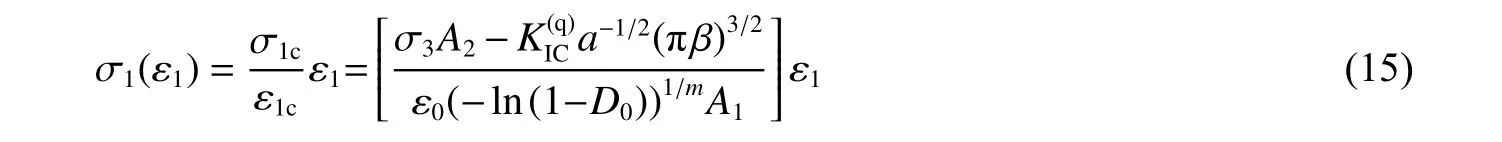
因此，综上所述，准静态荷载作用下，岩石完整的应力-应变本构关系可以表示为：

将裂纹极限长度llim代入式（7），岩石极限轴向应变ε1f可以表示为：

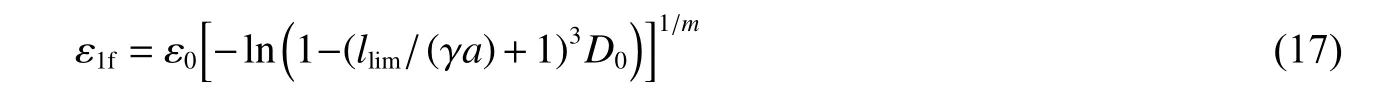
该极限应变对岩石失效应变提供一定参考。

1.2 准静态裂纹扩展与动态裂纹扩展的关系

式中：vl为裂纹速度（即dl/dt），vm为裂纹分叉速度，vm=RcR，该速度随着材料柔度增加而减小，瑞利波速cR= [E/(2ρ(1+ν))]1/2(0.87+1.12ν)/(1+ν)，cp为P 波速度，cp=[(1-ν)E/((1+ν)(1-2ν)ρ)]1/2，式中ν 为泊松比，ρ 为材料密度，E 为弹性模量，R 是材料常数（0＜R＜1）。

基于式（7）可以解出裂纹扩展长度表达式为：

对式（19）裂纹长度求时间导数，则可以推出岩石内部细观裂纹速率vl为：

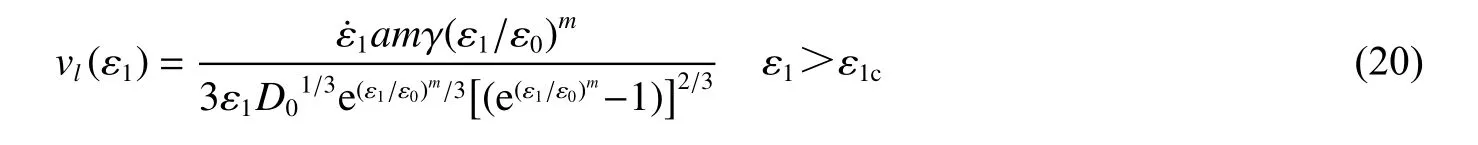
将式（20）代入式（18），则可以建立动态断裂韧度与宏观轴向应变率之间关系：

式中：

1.3 动态裂纹扩展下的应力-应变关系

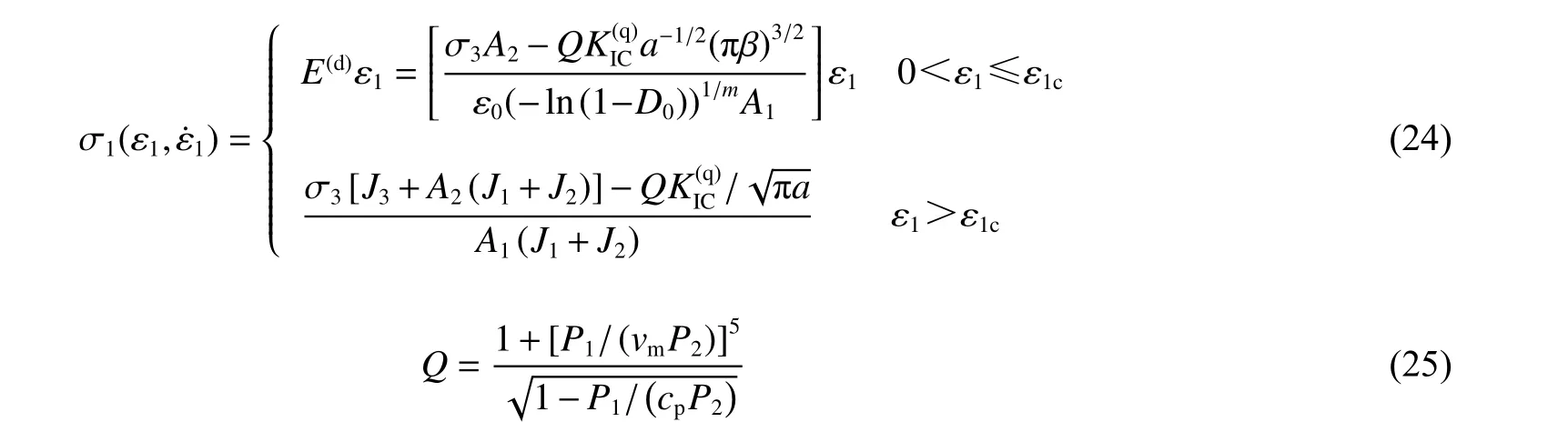
式（24）中E(d)为动弹性模量，下面将对模型参数对动弹性模量影响进行详细讨论。此外，值得注意的是在动弹性模量E(d)的方程计算中，参数Q 中的轴向应变ε1应取值为ε1c。

2 结果与讨论

2.1 动态应力-应变关系理论结果合理性验证

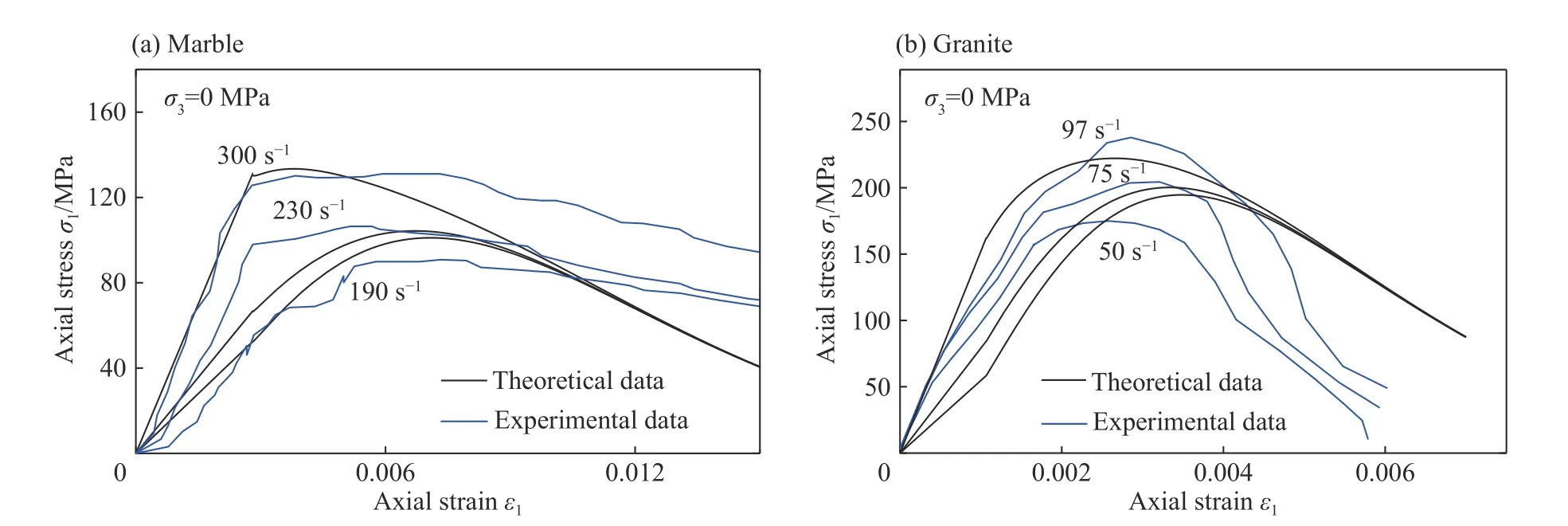
图 2 大理岩与与花岗岩动态应力-应变曲线的理论与试验结果[3, 23]对比Fig. 2 Comparisons between theoretical and experimental [3, 23] dynamic stress-strain curves in marble and granite

图2 中分别给出基于大理岩与花岗岩材料属性，得到的动态应力应变本构关系的理论与试验结果[3,23]曲线对比结果。可以看到，理论结果与试验结果在变化趋势上具有较好的相似性，在数值上具有一定的可比性，但是仍然存在一定的差异性。其中导致这些差异的原因可以分析为以下几点：（1）本文中提出的理论模型是一个基于各向同性的均匀弹性体得到的；（2）岩石内部随机分布裂纹无法真实呈现，而是通过假设裂纹尺寸、角度相同的均布化思路进行计算分析的。

2.2 应变率对应力-应变关系、动态压缩强度和动态弹性模量的影响

图 3 应变率影响下的应力应变本构关系Fig. 3 Effect of strain rate on stress-strain curve

以上通过试验结果验证了本文基于细观力学的动态本构模型合理性。下面将详细讨论应变率对岩石力学特性（动态压缩强度和动态弹性模量）的影响。其中模型参数选取参考花岗岩参数。图3中给出了不同应变率下，应力-应变本构关系的变化趋势。可以看到，随着应变率的增加，应力应变曲线峰值应力，即压缩强度，也在不断增大，而且是加速增加，该现象也可以通过图4 给出的轴向动态压缩强度与轴向应变率关系清楚地看到，该结果已经被众多研究动态强度理论的学者验证[1,3, 13, 15,23]。还可看到，随着应变率的增大，岩石动态强度对应峰值轴向应变不断减小。图4 中，研究了不同岩石内部初始损伤、模型参数m、ε0、R 下，岩石轴向动态压缩强度与轴向应变率的联系。随着初始损伤D0或参数ε0、R 的减小、参数m 的增大，在一定轴向应变率下轴向动压缩强度增大。

图 4 不同模型参数的应变率与岩石动态压缩强度关系Fig. 4 Relations between strain rate and dynamic compressive strength under different model parameters

此外，还可以看到，岩石裂纹初始应变值ε1c随着应变率增加为一个恒定值，而裂纹初始应变对应的裂纹初始轴向应力则是随着应变率的增加也在增大。本文中假设裂纹初始应变前的变形为线弹性变形。随着应变率增加，岩石弹性变形阶段曲线的切线模量，即动态弹性模量，在不断加速增大，该现象也可以在图5 中动态弹性模量与应变率之间关系看到，并且与众多学者的试验结果[1-3,23]相一致。图5 研究了不同围压、岩石内部初始损伤及模型参数m、ε0、R 下，岩石动态弹性模量与轴向应变率之间的联系。随着初始损伤D0或参数m、ε0、R 减小、围压增大，在一定轴向应变率下动态弹性模量不断增大。

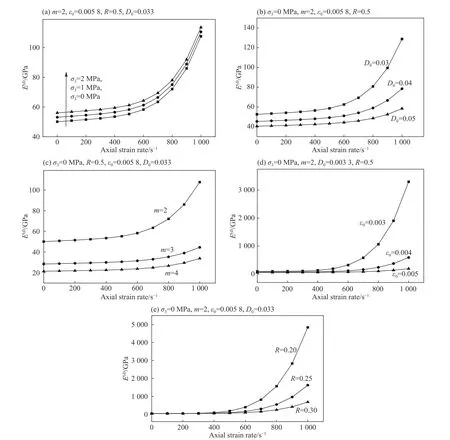
图 5 不同模型参数的应变率与动态弹性模量关系Fig. 5 Relations between strain rate and dynamic elastic module under different model parameters

2.3 模型参数敏感性分析

岩石内部初始损伤对岩石力学性能有着重要的影响。图6 中给出了不同初始损伤对于高应变率300 s−1下动态应力-应变本构关系曲线的影响。可以看到，随着损伤的增大，岩石的动态压缩强度不断减小，而且随着损伤的减小，峰值强度对应的峰值应变在不断减小。图7 给出了不同围压状态下，岩石动态应力-应变关系曲线结果。可以看到，随着围压增大，动态压缩强度也在不断增大。此外，图8、9 分别给出了模型中参数m 和ε0对动态应力-应变关系曲线的影响，可以看到，随着参数m 和ε0减小，峰值强度对应的峰值应变值在不断减小。图10 中给出了参数R 对应力-应变曲线的影响，随着R 的减小，峰值应力对应的峰值应变值都在不断减小。

图 6 初始损伤D0 对动态应力应变本构关系影响Fig. 6 Effect of initial damage on dynamic stress-strain constitutive relation

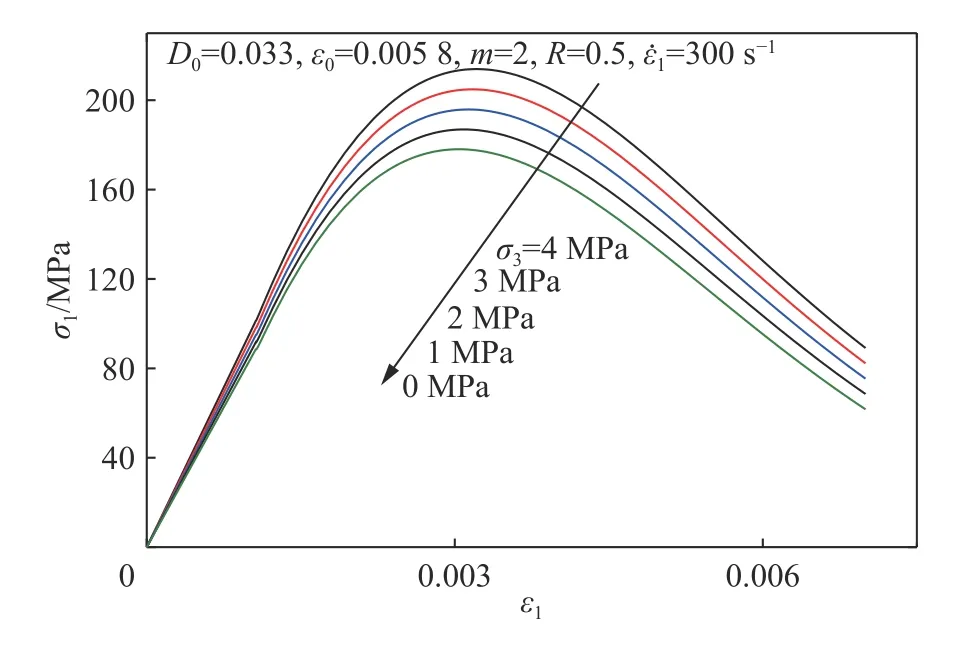
图 7 围压对动态应力应变本构关系影响Fig. 7 Effect of confining pressure on dynamic stress-strain constitutive relation

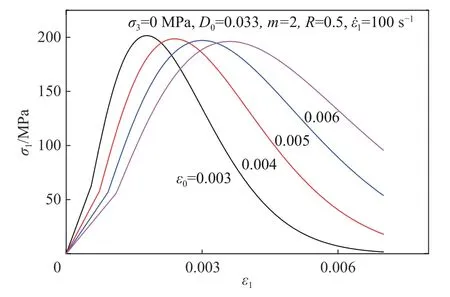
图 9 参数ε0 对动态应力应变本构关系影响Fig. 9 Effect of parameter ε0 on dynamic stress-strain constitutive relation

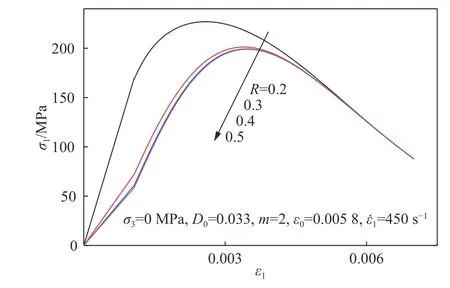
图 10 参数R 对动态应力应变本构关系影响Fig. 10 Effect of parameter R on dynamic stress-strain constitutive relation

图11 中，给出了不同应变率下，动态弹性模量与围压、初始损伤和参数m、ε0、R 的关系。可以看到，随着围压的增大，动态弹性模量线性增大；随着初始损伤和模型参数m、ε0、R 的增大，动态弹性模量在减速降低。以上关于模型参数影响研究，更加清楚详细地分析了本文提出的宏细观力学模型中参数敏感性。进而为更加精确地建立真实岩石与模型关系之间联系提供了一定的参考。

图 11 应变率对不同模型参数与动态弹性模量关系影响Fig. 11 Effects of strain rate on the relationships between model parameters and dynamic elastic modules

3 结 论

基于脆性岩石准静态裂纹扩展作用下的应力-应变本构关系、裂纹速率与应变率的变化关系及裂纹速率与断裂韧度的关系，建立了基于细观力学的动态应力-应变本构关系模型。通过试验结果验证了模型的合理性，并讨论了模型参数对岩石动态压缩力学特性的影响。具体结果如下：

（1）随着应变率的增大，岩石动态压缩强度不断增大，岩石裂纹初始应力不断加速增大，峰值轴向应力对应的峰值轴向应变值不断减小，岩石动态弹性模量不断加速增大。

（2）随着围压，初始损伤D0，参数m、R 和ε0的减小，应力-应变曲线中峰值强度对应的峰值应变不断减小。

（3）随着初始损伤D0或参数ε0、R 的减小，围压或参数m 的增大，在一定的轴向应变率下，轴向动态压缩强度在增大。

（4）随着初始损伤D0或参数m、ε0、R 的减小，围压的增大，在一定轴向应变率下，动弹性模量不断增大。