时程稳定性系数确定的边坡逐孔起爆孔间微差降振时间*

周文海，梁 瑞，陈金林，朱 冕，陈鹏辉，楼晓明，王敦繁

（1. 兰州理工大学石油化工学院，甘肃 兰州 730050；2. 紫金矿业集团股份有限公司紫金山金铜矿，福建 龙岩 364200；3. 福州大学爆炸技术研究所，福建 福州 350116；4. 浙江大学海洋学院，浙江 舟山 316021）

选取合理的台阶逐孔微差爆破延期时间，可以降低地表质点振动，改善爆破质量，节省工程投入成本；自20 世纪中叶，通过控制微差时间降低爆破振动危害和改善爆破质量方面有了大量科学研究[1]。田振农等[2]采用时-频分析方法，对隧道爆微差破振动的一般特征进行了研究，发现：由于雷管段数的限制，起爆网络经常被分成几个时段，造成振动波无规律叠加，以至出现多个峰值现象；但是如果技术措施合理，能使爆破振动速度峰值显著降低，在此基础上根据雷管起爆延时精度高的特点并借鉴干扰减振的思路，提出的错相减振机理，对微差起爆振动效应起到了有效控制。Johansson 等[3]通过微差控制小炮实验对孔间冲击波相互作用进行研究，通过大量研究数据表明，微差时间选取（0～1.1 W ms）时降振效果明显优于2 W ms 及以上，其中W 为最小抵抗线（单位为m）。龚敏等[4]以南方某城市隧道工程为背景，进行现场单孔单自由面爆破实验，获得不同药量-微差时间振动曲线，再利用MATLAB 程序，根据每段不同延时范围，将两单孔曲线按相邻段起爆的多个微差间隔进行不同振动叠加，选择其中最大振速的合成曲线与单孔振动曲线按下一相邻孔的微差间隔进行新的振动合成，最终得到微差掏槽爆破后的累积叠加曲线，以此与现场实测振动曲线比较，得出微差起爆间隔较大的合成振速并不一定比小间隔起爆的振速小，合成振速是否超标取决于起爆药量(或相应振动曲线)、微差间隔时间、规定振速值三者的量化关系。Anderson 等[5]运用统计分析理论，对大量微差爆破工程实例资料进行分析研究，最终利用灰度图反演了微差时间与振动波主频之间关系，以此划分出了不同微差时间对于地表振动的影响程度和范围。杨年华等[6]将现场试爆单孔药包引起的振动波作为基波，按照不同比药量的比例系数对基波进行折算得到实际施工振动波谱，然后按不同微差时间利用振动波线性叠加理论对折算后的振动波谱合成，以此达到对峰值振动强度预测和对最佳微差时间进行判定的目的。本文中，先通过有限元法确定自然状态下二维边坡潜在滑动面以及静态安全系数，再基于二维静力模型重新建立三维爆破模型，反演冲击载荷作用下潜在滑动面受力情况，并提取相应的滑面单元应力数值，结合传统极限平衡法绘制出冲击载荷作用下边坡稳定性系数曲线，最终确定出最佳孔间降振微差时间。

1 冲击载荷作用下安全系数计算方法

通常有两种方法用于边坡稳定性分析，一种为极限平衡法，另一种则是有限元法。极限平衡法将滑坡体看作理想塑性材料的均质刚性体，计算过程对边界条件大大简化，且完全不考虑岩土体本身应力-应变关系，因而很难真实反映边坡失稳状态下位移场和应力场的变化情况；而有限元法则考虑了岩土体应力-应变关系，且不需要预先设定滑动面，能够真实有效地反映岩土体边坡失稳状态。因此，本文中先利用有限元法确定潜在滑动面，提取滑动面单元上的应力 σx、 σy、 τxy，再结合极限平衡法求 得边坡体在冲击载荷下的动力稳定性系数，如图1所示。

极限平衡法以摩尔-库伦抗剪强度理论为基础，对潜在滑动面进行条块划分，在各条块上建立平衡方程，将潜在滑动面上抗滑力和滑动力的比值f 与定义为安全系数：

式中： τf为岩土体抗剪强度； τ为岩土体剪应力。

运用有限元法确定潜在滑动面时需要定义岩土体本构模型，而ANSYS 程序中自带多种屈服破坏准则，岩土体材料通常选用摩尔-库伦准则或广义米塞斯准则（D-P 准则）[7]。在考虑静水压力情况下，将米塞斯准则进行推广就转换成D-P 准则：

式中： σ1、 σ2、 σ3分别为第一、二、三主应力； I1为应力张量第一不变量； J2为应力偏张量第二不变量； α、k为模型材料与内摩擦角 φ′和凝聚力 c′相关系数。

基于有限元计算结果，可提取滑面单元上的应力 σx、 σy、 τxy。 切向应力τ 和法向应力 σn为：

式中： α 为 x轴与所求滑面单元切线方向夹角。

由摩尔-库伦准则，可得所求滑面单元抗剪强度为：

式中： c′为岩土体凝聚力； φ′为岩土体内摩擦角。

将整个边坡潜在滑动面单元按式（1）进行积分运算，可得边坡整体安全系数公式为：

式中： l为潜在滑坡面弧段长度。

2 按实体模型进行数值模拟

2.1 按实体模型建模

以西北某露天采场临时边坡为原型进行数值模拟，建模所用材料参数以爆破施工现场的具体情况为准。其中，模拟过程所采用的岩石力学性能源于该矿区地质资料中的爆区附近采样点数据，爆破工艺参数和模型尺寸与施工情况一致，其边坡高度24 m，坡面角70°，孔径150 mm，孔深14 m，堵塞长度5 m，底盘抵抗线根据钻孔作业安全条件 W=H cotα+B以台阶高度12 m 来设计，取W=7 m（H 为台阶高度、 α为台阶坡面角；B 为钻孔中心至坡顶线安全距离取2.5 m），孔排间距选用5 m×6 m 的孔网参数。岩石材料选取典型的弹塑性材料，即采用MAT_PLASTIC_KINEMATIC 模型；堵塞物选用土壤材料MAT_SOIL_AND_FOAM 模型；炸药选取2#岩石乳化炸药，其材料类型为HIGH_EXPLOSIVE_BURN，炸药状态方程选取不考虑炸药产物成分的EOS_JWL 方程。为提高模拟运算效率，在不影响计算精度和分析结果的基础上：首先通过ANSYS 软件建立自然状态下二维实体边坡静力模型，运用有限元折减法确定潜在滑动面；然后依据二维静力模型，重新建立同性质同尺寸的三维爆破模型，通过LS-DYNA 软件进行逐孔微差爆破动力分析；整个模拟过程所用爆破参数、岩土力学参数和边坡结构参数按照现场实际取值。模拟过程炸药爆炸时的JWL 状态方程[8]为：

式中：A、B、 R1、 R2、 ω为 材料常数，p 为压力，V 为相对体积， E为初始比内能。

岩石主要力学参数分别为：岩土密度为2.78 g/cm3，弹性模量E=18.23 GPa，抗压强度σ0=76.2 MPa，泊松比µ=0.23，内聚力为17.6 MPa，内摩擦角φ=33°36'。炸药主要参数分别为：密度为0.95 g/cm3，爆速为3.6 km/s，爆轰压力为3.61 GPa，A=47.6 GPa，B=529 MPa，R1=3.5，R2=0.9，E=4.5 GPa，V0=1 cm3。

郑颖人等[7]、Griffiths 等[9]通过对比研究指出，有限元模拟时模型边界范围取值对于计算结果的影响较极限平衡法更敏感，且给出较理想的模型范围取值为：边坡上下边界高度应超出坡高2 倍以上，右边界距坡顶线距离取坡高2.5 倍左右长度，左边界距坡脚处距离取坡高1.5 倍左右长度；因此，将三维实体边坡模型进行拓展，上下边界取50 m，左边界距坡脚距离取36 m，右边界距坡顶线距离取60 m，边坡厚度取50 m，模型三维示意图和参数平面图如图2～3 所示。

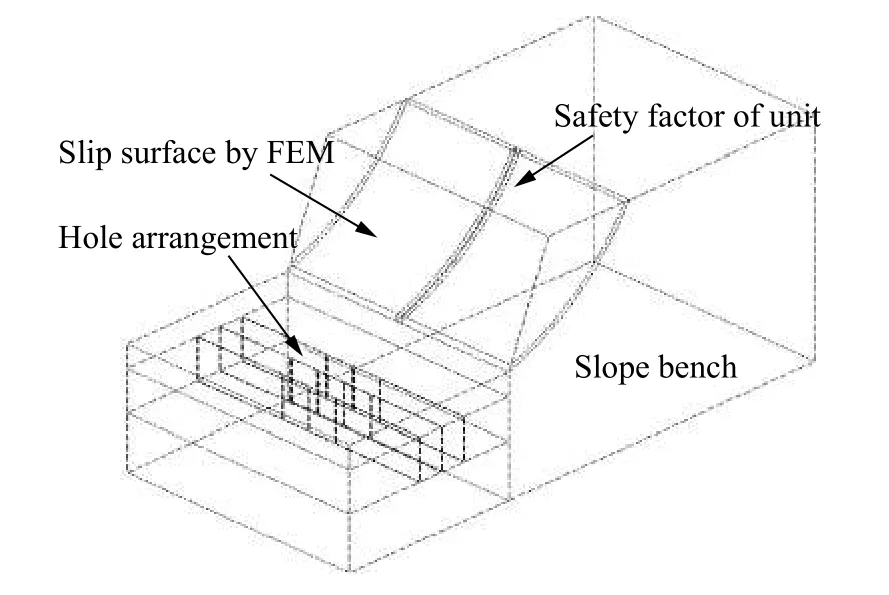
图 2 三维有限元计算模型Fig. 2 3D finite element model of slope

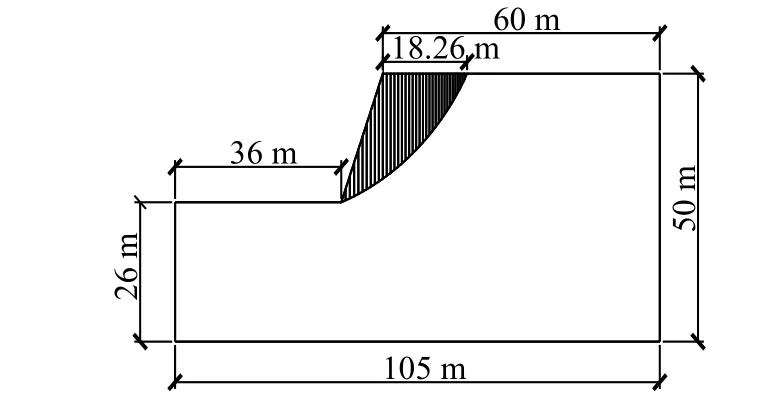
图 3 模型参数Fig. 3 Model parameters

2.2 单元类型选取、网格划分及施加载荷

二维建模采用四节点的PLANE82 单元和理想弹塑性模型（D-P 模型）；三维建模静力分析时采用八节点隐式实体单元SOLID 185，动力分析时采用显示分析和八节点SOLID 164 实体单元，材料定义为理想弹塑性模型。模型网格划分严格按照二维状态四边形、三维状态六面体进行，二维、三维模型划分单位数分别为4 521 和170 958。在施加约束和载荷方面：二维模型边坡面和顶部定义为自由边界，左右边界面施加位移约束，运算过程一直保持重力加载；三维模型边坡面和顶部同样定义为自由边界，其余均为透射边界，运算过程保持动力松弛加载预应力且全程施加重力载荷。二维、三维网格划分如图4～5 所示。

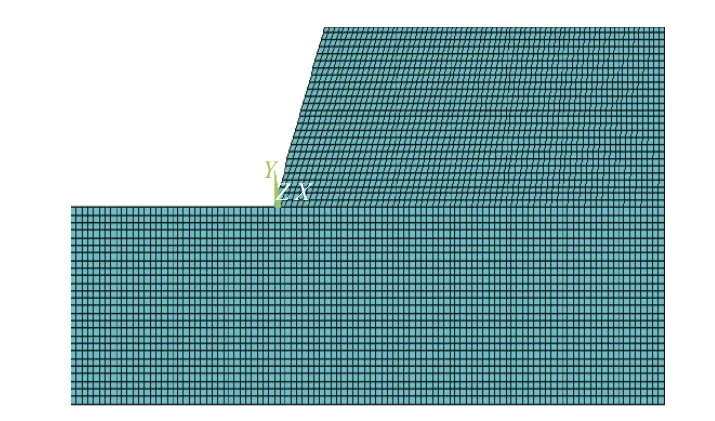
图 4 二维模型网格划分Fig. 4 Mesh generation of 2D

图 5 三维模型网格划分Fig. 5 Mesh generation of 3D

2.3 自然状态下静态安全系数的确定

采用强度折减法判定边坡是否失稳的充要条件为：滑动面贯通于塑性应变区、滑动面上节点位移或塑性应变发生突变、有限元方程组无解且计算结果不收敛[10-15]。依据有限元强度折减原理，先选取初始折减系数为1，将岩土体强度参数（内摩擦角、黏聚力）进行折减，当第8 次折减运算时（ f=2.750），潜在滑动面处于临界破坏状态，直到安全系数取 f=2.780 时滑动面上节点位移发生突变且贯通于塑性应变区，有限元计算结果不收敛。具体塑性应变如图6 所示，折减过程参数变化见表1。

将强度折减法计算得到的潜在滑动面按照传统极限平衡法进行条块划分，并且计算条块滑弧每个单元长度和滑弧面上的切线与x 轴的夹角θ，进行边坡稳定性验证分析。通过计算分析发现：二维有限元临界安全系数为2.750，三维有限元临界安全系数为2.610；传统极限平衡法中瑞典条分法确定的临界安全系数为2.525，简化Bishop 法确定的临界安全系数为2.505，Jonbu 确定的临界安全系数为2.679。因此，有限元法确定的临界安全系数与传统极限平衡法确定的临界安全系数相对误差在8%以内，计算结果较接近。各计算方式得到的安全系数见表2。

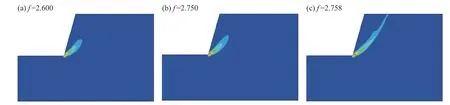
图 6 塑性区域分布Fig. 6 Plastic regional distribution

表 1 折减算法Table 1 Strength reduction method

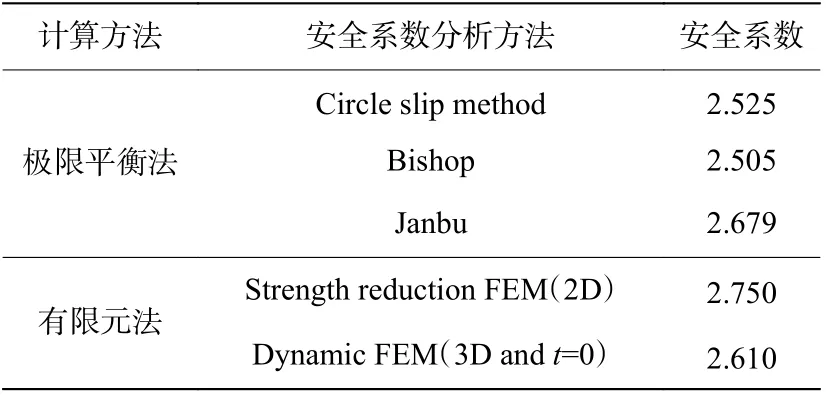
表 2 各种计算方式的安全系数Table 2 Safety factor for each calculation method

2.4 冲击载荷作用下动态安全系数的确定

根据二维模型得到的边坡滑动面，依据同等尺寸重新建立同等条件下的三维逐孔微差爆破模型，将边坡潜在滑坡弧面进行等长条分，取三维台阶中间剖面进行网格细分，共等分为37 个单元；台阶面同排设置3 个炮孔微差起爆，孔间微差时间分别取0、17、25、42 和65 ms，如图1～2 所示。利用ANSYS 软件进行显式-隐式转换，通过动力松弛分析，得到边坡在重力作用下的原始应力场；将ANSYS 隐式求解结果导出的动力松弛文件导入LS-DYNA 中进行后续动力分析，3 个炮孔同时起爆某个时刻三维应力云分布如图7 所示。

图 7 应力分布Fig. 7 Stress distribution

对3 个炮孔同时起爆过程中模型质点的应力、位移进行分析，发现：起爆初期炮孔壁压力急剧增大，最大值可达1.36 GPa，直到约60 ms 孔壁压力基本趋于稳定，孔壁单元应力明显高于坡面应力；坡脚处出现应力集中现象，应力明显高于其他质点，但应力集中效应瞬间消失后趋于稳定。坡顶质点位移波动幅值高于坡面和坡脚位移约3 倍，坡顶位移波动幅值分布于−0.35～0.25 cm，这主要是应力波在自由面处的反射拉伸作用和尖端放大效应所致。

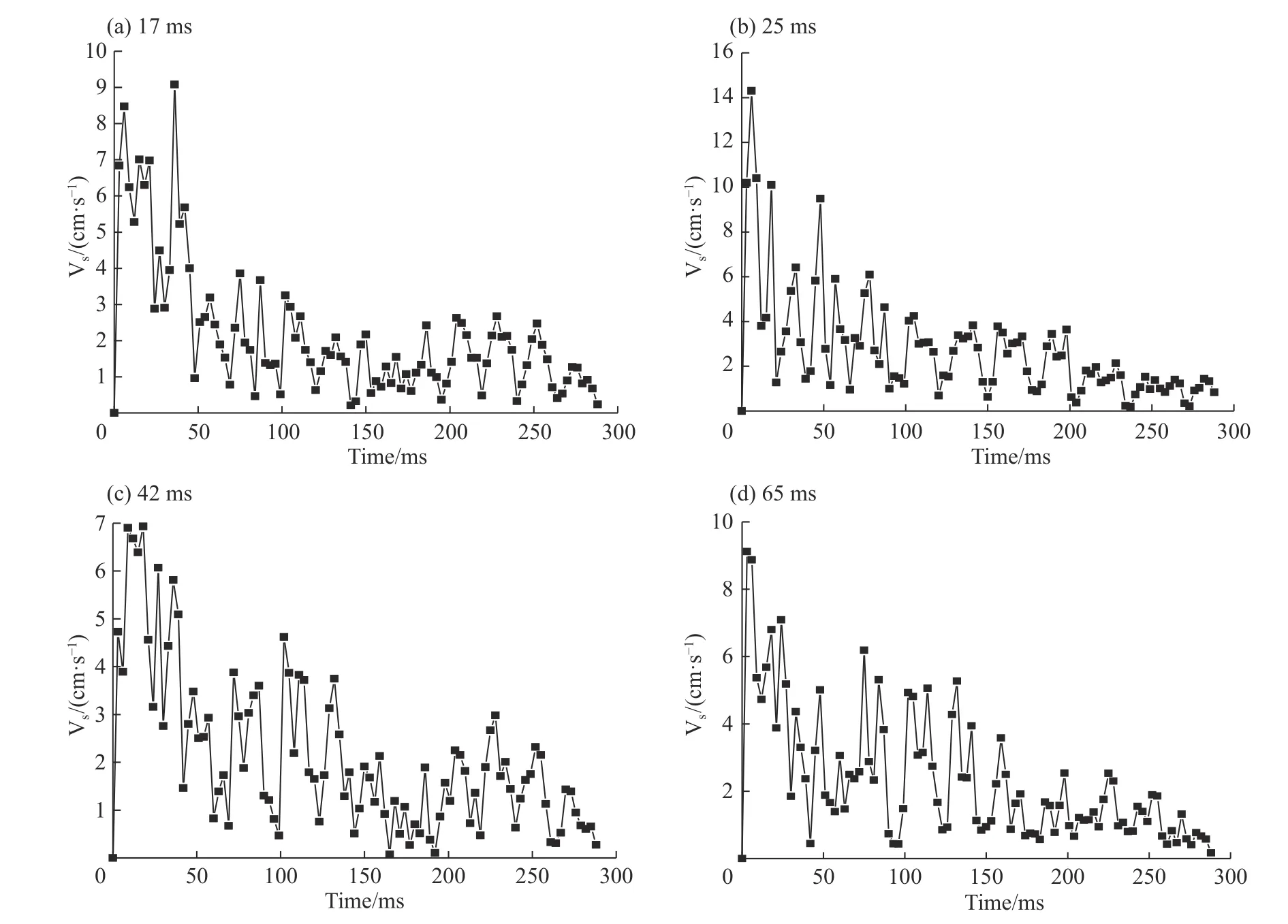
图 8 微差起爆合速度衰减规律Fig. 8 Resultant velocity attenuation regularity of millisecond detonating

依据楼晓明等[16]提出的逐孔微差爆破振动波峰值合速度-位移分布特征理论，可将爆破振动过程中地表质点三轴振动峰值合速度， Vs,max作为地表质点振动大小判据；因而在滑坡弧中间剖面提取其中某个单元观测其合速度 Vs变化规律，通过观察发现17、25、42 和65 ms 不同孔间微差延期起爆时对应的 Vs,max分别为9.08、14.3、6.93 和9.12 cm/s，说明选用42 ms 孔间微差延期起爆时间能够起到更好的降振效果。4 种微差起爆 Vs衰减规律如图8 所示。

图 9 边坡稳定性系数曲线Fig. 9 Slope stability coefficient curve

2.5 安全系数曲线确定微差时间

利用后处理软件提取3 个炮孔同时起爆时滑面单元爆炸过程中的应力 σx、 σy、 τxy；在1～300 ms 运算时间段内，每隔3 ms 输出一次，共计100 组数据，利用式（5）～（8）求解动态安全系数，并绘制出边坡稳定性系数曲线，如图9 所示。

由图9 可知，药包起爆后在0～21 ms 时间段，内应力波还未集中作用于边坡潜在滑动面，只有少部分应力波抵达该部位，所以该时间段内边坡动态安全系数基本和自然状态下静态稳定性系数保持一致。随着时间推移，在爆炸冲击载荷作用下边坡动态稳定性发生较大波动，当t=48 ms 时动态稳定性数达到最大值 f =7.623，当t=102 ms 时动态稳定性系数达到最小值 f=1.375，直到240 ms 左右趋于稳定。

从先爆炮孔产生的冲击载荷集中作用于边坡潜在滑动面开始，到该潜在滑动面稳定性系数达到最大值（最稳定状态）为止，将该时间间隔步长作为后续炮孔起爆的孔间最佳降振微差时间较合理。通过本文选取的实际边坡爆破模型进行孔间同时起爆数值模拟发现，21 ms 时冲击载荷集中作用于边坡潜在滑动面，48 ms 时动态稳定性系数达到最大值；因此，对于该模型选用孔间微差爆破技术时，最佳孔间降振微差时间应为48 ms。

3 测振实验选取降振微差时间

在相同露天采场临时边坡平台，进行了4 次与模拟情况相似的等比例不同段别雷管组合的小炮爆破测振实验，4 次实验所选用的部分爆破工艺参数取值与模拟参数比约为1∶2。小炮实验的孔径80 mm，孔深7 m，堵塞2.5 m，底盘抵抗线W=4 m，孔排间距选用3 m×4 m 的孔网参数，装药结构为无间隔耦合装药。4 次实验排间统一选用3 段25 ms 延期雷管，孔间分别采用2、3、4、5 段雷管控制微差时间，即组成排、孔间（25 ms，17 ms）、（25 ms，25 ms）、（25 ms，42 ms）、（25 ms，65 ms）的微差起爆方式；试爆时，采用爆破测振仪对距爆区空间距离约270 m 范围进行测振，每次测振区布置4 个临近监测点，分别记为A、B、C、D，测振所得峰值速度数据和4 次监测中A 测点合速度衰减规律见表3和如图10 所示。

通过对4 次微差试爆区16 个测点测得的三轴峰值合速度数值分析发现：孔间选取17 ms 微差起爆时，4 个监测点测得的峰值合速度最大值为1.294 1 cm/s，最小值为1.067 7 cm/s；孔间选取25 ms 微差起爆时，4 个监测点测得的峰值合速度最大值为1.702 1 cm/s，最小值为1.387 8 cm/s；孔间选取42 ms微差起爆时，4 个监测点测得的峰值合速度最大值为0.630 6 cm/s，最小值为0.503 1 cm/s；孔间选取65 ms 微差起爆时，4 个监测点测得的峰值合速度最大值为0.943 7 cm/s，最小值为0.865 5 cm/s。测试结果显示，孔间选取42 ms 微差时间延期起爆时测点三轴峰值合速度幅值明显低于其他3 种情况，依据峰值合速度-位移分布特征理论，可证实4 种测振实验中孔间微差时间取42 ms 时引起的地表质点振动最小。

表 3 不同孔间微差时间下监测点峰值速度Table 3 Monitoring point’s peak speed at different hole millisecond time

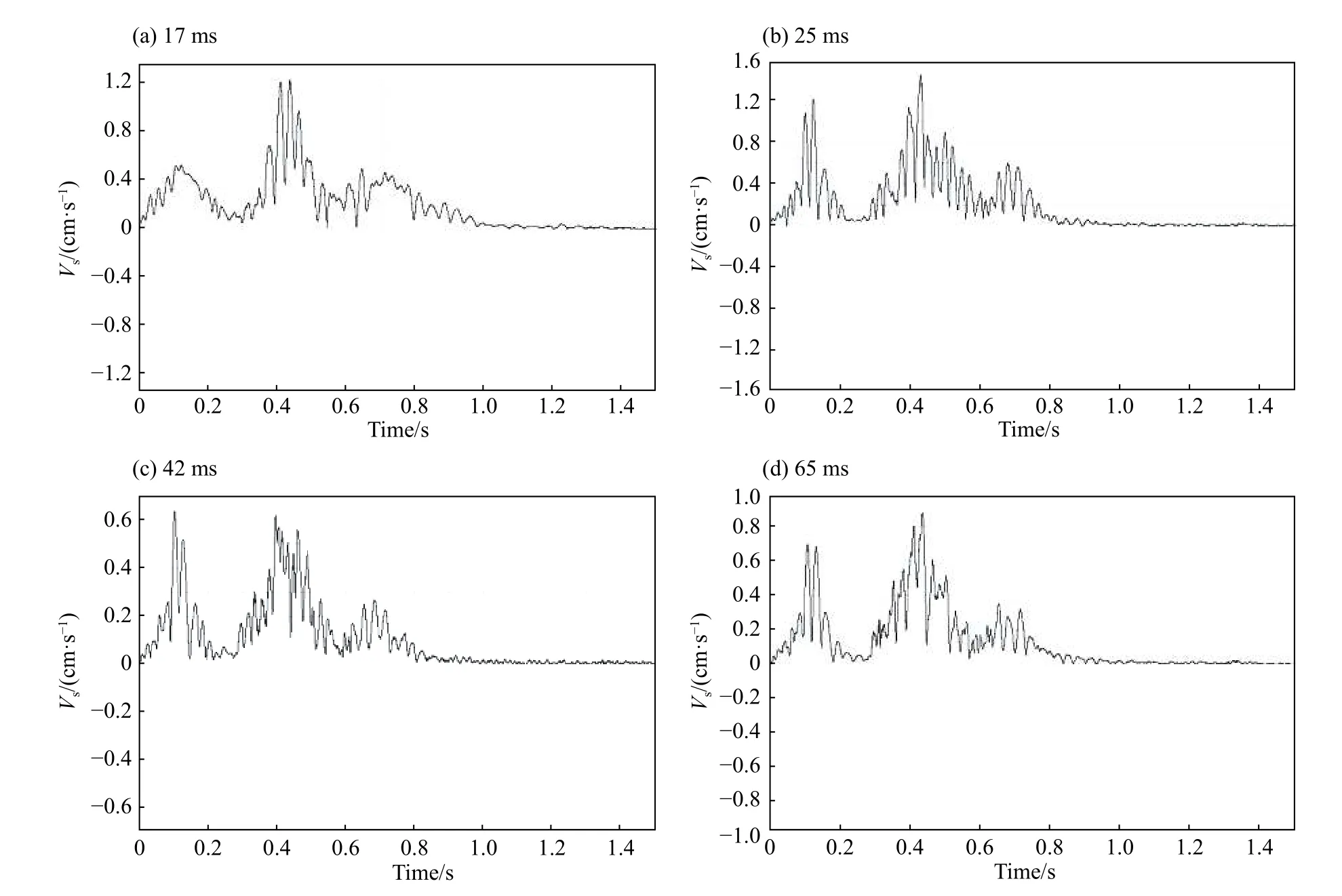
图 10 不同孔间微差起爆时测点A 合速度衰减规律Fig. 10 Resultant velocity attenuation regularity of measuring point A with different millisecond detonating

4 结 论

(1)研究爆破施工对边坡稳定性影响时，可先运用有限元法建立二维静态边坡模型确定潜在滑动面，然后在已确定的潜在滑动面基础上建立三维爆破模型，同时采用LS-DYNA 软件对冲击载荷作用下边坡稳定性进行动力分析。

(2)在模拟结果中，提取冲击载荷作用下边坡滑动面单元应力，将该应力代入传统极限平衡法计算公式，绘制出边坡稳定性系数曲线；通过对该曲线分析发现，可将冲击载荷集中作用于边坡滑动面开始到该滑动面稳定性系数达到最大值之间的时间步长作为孔间最佳降振微差时间。

(3)通过对某个实际边坡稳定性系数曲线理论分析发现，最佳降振微差时间为48 ms，而通过不同微差时间控制的数值模拟和现场测振实验得到最佳降振微差时间为42 ms；该理论分析结果与模拟和实验结果较接近，说明采用边坡动态稳定性系数曲线确定的最佳降振微差时间较可靠，可为类似工程项目提供理论依据。