基于GNSS的高轨飞行器定轨研究
王立强 董 剑 席福彪 于海霞 李元元
1.中国运载火箭技术研究院研究发展部,北京100076 2.大连海事大学船舶电气工程学院,大连116026 3.北京市电信工程局有限公司,北京 100061
目前,高轨飞行器的定轨是利用地面S波段统一测控系统(USB)进行的,设备复杂、成本高。近年来,利用星载GPS接收机对中低轨道(3000km以下)进行定位的技术已经成熟,并已部分应用到中低轨卫星的定位中。然而,当轨道高度高于4000km左右后,接收正面的单一导航卫星星座卫星信号无法正常接收到4颗卫星,因而无法定位。近年来,国外提出了利用接收卫星旁瓣或接收地球另一面卫星的方法提高接收卫星的数量,这对卫星接收机的灵敏度、可见性等都提出了更高的要求,当前国外已有多例高轨卫星星载GPS接收机飞行试验,并已取得了部分成果。1997年,TEAMSAT和EQUDATOR-S论证了高于GPS卫星星座的GPS信号闭环跟踪能力,包括在海拔超过60000km时返回测量数据,以及对旁瓣信号的跟踪[1]。同年,Falcon Gold卫星在同步转移轨道成功使用一个低功率的数字取样接收机记录了GPS信号。2000年,基于GPS的美国国防部地球同步轨道系统的成功论证首次公开。2001年,AMSAT OSCAR-40的试验结果进一步证明了基于GPS的高轨定位是可行的,并增强了未来高轨GPS用户对信号特征的理解。国内方面,已有单位开展了地球同步轨道卫星接收机的研制,提出利用一颗卫星的伪距测量参数,加上动力学模型进行GEO卫星的定轨,但受卫星数量的限制定轨精度约几百米[2]。
主要研究GNSS系统实现高轨飞行器导航定位的解决方案,包括可见性分析、信号功率计算等,提出利用多星座组合的导航方案,并通过仿真验证了组合导航解决高轨导航的可能性。
1 存在的问题
高轨飞行器对GNSS卫星的可见性主要取决于以下几个因素:1)GNSS卫星的发射功率及天线方向图(主瓣、旁瓣);2)GNSS卫星与飞行器的位置关系及距离;3)GNSS接收机本身的灵敏度。
卫星导航设计主要是针对地面用户,为其提供连续、实时及高精度的定位导航服务,所以卫星发射天线朝向地球。在LEO(低地球轨道,3000km及其以下范围),导航系统的可见卫星多,信号条件好;而对于高轨的轨道高度一部分轨道高于卫星星座,一部分低于卫星星座。当轨道高度超出卫星天线覆盖范围,它只能接收来自地球另一面的导航卫星发射的信号或卫星旁瓣信号。这样,绝大部分卫星发射天线主瓣信号就会由于地球的遮挡而无法到达地球的另一面,只有在导航卫星天线下行频率主波束边缘构成的环形锥内才能收到卫星信号[3]。如图1所示,GPS发射天线的主瓣波束宽度为42°,而地球遮挡GPS信号的半锥角为13.9°,飞行器只有在GPS 发射天线主瓣波束边缘构成的环形锥内才能收到GPS信号,由此,飞行器的GPS可见星数量大大减少,同时高轨飞行器要从地球另一面接收GPS信号,信号传输距离增加,信号减弱,增加了接收难度。

图1 对GTO轨道及GEO轨道覆盖示意图
2 卫星可用性判断
以2个标准作为判别GPS星是否可见的条件:①导航星可见性,即几何条件满足要求;②信号强度满足要求。
2.1 导航星可见性
当用户接收地球正面的卫星(不考虑地球的遮挡),直接判断用户是否在导航星的主瓣或旁瓣内;当用户接收地球背面的卫星,判别从导航星到用户星的信号传播过程中信号是否受到阻挡,主要看是否受到地球的阻挡。判别的标准是导航星的信号发射半角At是否大于要被阻挡的那部分半角。对发射半角At的设置不仅考虑到了发射半角主瓣信号的接收,也考虑到旁瓣信号的接收,因为这样可能有利于增加可见星数目,特别是在接收机门限值较低的情况下,从国外的研究成果来看,增加的可见星数目将比较可观,而且国外的数次高轨道搭载试验也验证了确实能够接收到GPS星的旁瓣信号,而At的计算通过以下公式进行:
(1)
其中,enu为GPS星指向用户星的矢量;rgps为GPS星指向地心的矢量。
2.2 导航信号可用性
为了利用导航卫星的旁瓣信号,必须计算导航接收机信号的信噪比,接收机接收到的信噪比与卫星发射功率、发射天线增益、链路损耗、接收天线增益以及卫星与飞行器相对位置等诸多因素有关:
1)等效发射功率(EIRP)
EIRP与卫星功放输出的功率Pt以及发射天线增益Gt有关,即:
EIRP=Pt(dBW)+Gt(dB)
(2)
2)自由空间损耗(LD)
卫星信号的电波在空间传播中受到损耗,最主要的是自由空间的传播损耗,它占总损耗的绝大部分,传播距离越大,自由空间的损耗越大,其公示表示为:
LD(dB)=92.45+20log(d*f)
(3)
其中,d为距离,单位km;f为频率,单位GHz。
3)接收机接收信噪比
S/N=EIRP-LD+Gr-10lgKTRb+LNF
(4)
各符号的含义及数值参见表1。

表1 典型空间链路参数计算方法
3 多星座组合导航
目前,采用单一的导航定位系统和普通接收机无法满足定位的可见星要求,可以采用BD2/GPS/GLONASS/GALILEO多星座组合的方式,提高GNSS接收机的定位精度和可靠性。
3.1 多星座组合导航定位原理及其参数分析
卫星导航定位方法的实质是以星地空间距离为半径的三球交汇,以卫星和用户接收机天线之间的距离观测量为基准,根据已知的卫星瞬时坐标确定用户接收机天线的位置。由于卫星导航系统采用单程测距原理,卫星钟与用户接收机时钟之间难以保持严格同步,受卫星钟和接收机时钟同步差的共同影响,实际观测量是含有误差的伪距。一般将接收机的钟差作为一个未知参数与观测站坐标在数据处理中一并解出,因此为了实时求解用户位置至少需要同步观测4颗卫星。
BD2、GPS、GLONASS和GALILEO组合导航定位,即接收机同时接收这些导航电文信息,根据接收到的导航电文信息计算得到卫星在空间的瞬时位置坐标,结合测量获得的用户到卫星的相对距离,利用多球定位原理计算出用户在空间的位置,实现高精度的定位和导航。需要注意的是,由于各系统之间存在时间偏差,以及坐标系不同,在多星座组合导航中首先要统一时间和空间参考系。
在多星座组合定位系统中,由于不同的坐标系得到的数据格式和结果都有差别,必须将四者转换到统一的时间和坐标基准下进行解算。各种导航系统的参数比较见表2。

表2 GNSS参数比较表
多星座卫星组合定位算法的基本思路是将各星座卫星的观测量融合到同一个方程组当中,进而联合求出导航解。如图2所示,将GPS、GLONASS、GALILEO和BD2的原始观测数据同时输入数据处理器中。将这些数据进行格式转换、时间转换、坐标系转换及伪距组合,然后统一求解,4种定位系统的组合、互相配合与补充,极大地提高了定位的可靠性。

图2 多星座组合导航定位流程图
3.2 多星座组合系统观测方程和坐标转换
导航卫星测码伪距的观测方程可写为:

(5)
式中,(x,y,z)和(xsi,ysi,zsi)分别是用户和卫星i在地球坐标系中的位置坐标。
为解算用户的实时位置,对3个坐标系间的直角坐标进行转换,要综合考虑坐标原点的平移、坐标轴之间的旋转以及由于各直角坐标系的刻度单位不尽相同而引起的尺度变化。目前采用最多的是七参数布尔萨(Bursa)转换公式,其转换公式为:
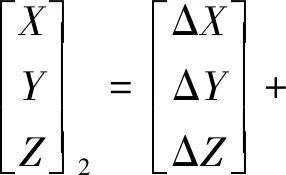
(6)
式中,ΔX,ΔY和ΔZ是坐标原点平移引起的3个平移参数;ΩX,ΩY和ΩZ是坐标旋转引起的3个旋转参数;k是尺度变化参数。
3.3 多星座组合系统定位解算
假设将4个系统的时间和坐标都统一到GPS 系统,则观测方程可统一成如下形式:

(7)



(8)

由以上模型可知,对于不同的星座和不同的可见星,观测方程组(8)中包含了δxu,δyu,δzu,cΔtGPS,cΔtBd和cΔtgls共6个未知数,当同时观测到6颗以上导航星时,可得冗余代数方程,用最小二乘法进行迭代求解和补偿,即可实现用户定位解算。
假设观测到n颗GPS卫星、m颗BD2卫星、k颗GLONASS 卫星和l颗GALILEO卫星,则组合定位方程的矩阵形式及其解形式可以分别表示为:
AX=B
(9)
X=(ATA)-1ATB
(10)
4 高轨卫星可见性仿真计算
对于星载导航系统的高轨卫星天基定轨方案,考虑基于多个导航系统的情况,采用BD2,GPS,GLONASS及Galileo共4个导航系统(虽然Galileo导航系统目前不可用,但是轨道分布及参数都基本上设计完成,可以通过仿真软件仿真导航卫星轨道)。假设接收机灵敏度可以接收卫星发射天线旁瓣,对GEO轨道接收BD2、GPS、GLONASS和Galileo卫星情况进行仿真如下:

图3 GPS GEO可见卫星数

图4 组合GNSS GEO可见卫星数
从仿真结果可以看出:位于GEO的高轨飞行器在其某些飞行阶段,GPS导航星座中的某些导航星虽然几何关系上可见,但是由于信号衰减的影响,这些导航星的信号不能用于导航解算。因此,对于完成GEO载荷发射任务的火箭,其飞行过程中,能够采用GPS进行导航的时间和空间范围是有限的,只有在少数特定的时间和空间内可用。若要满足定位的可见性要求,可以采用2种方式解决可见性问题:①采用多个GNSS系统组合的方式,增加可见导航卫星的个数;②通过采用高灵敏度的GNSS接收机跟踪的动态性进行特殊设计。受接收机灵敏度的限制,若要使单一导航系统满足全天时的要求也是非常困难的。
5 结束语
卫星导航在中、高轨道航天器的定轨研究是一个卫星导航应用的崭新领域。本文对中、高轨道航天器应用GNSS自主定轨技术的主要问题以及特点进行了分析,针对可见星少、GPS信号弱等难点,给出了相应的解决方案。本文的研究对中、高轨道,如GEO、HEO轨道卫星的定轨领域有重要作用,在卫星定轨、月球探测器近地段导航等应用有参考价值。

