不同工况下空穴效应对滑动轴承润滑性能的影响*

朱桂香 李 彪2 付杨杨3 孙 军3 朱少禹3 任燕平

(1.潍柴动力股份有限公司 山东潍坊 261001；2.合肥工业大学机械工程学院 安徽合肥 230009；3.合肥工业大学汽车与交通工程学院 安徽合肥 230009)

径向滑动轴承是各种机械设备中最主要摩擦副之一，其工作状况对设备工作经济性、可靠性和耐久性等性能有着非常重要的影响。随着中国制造2025制造强国战略的提出，对机械设备的发展和要求不断提高，工作条件更加苛刻，均对径向滑动轴承的设计水平提出更高的要求。

国内外研究人员一直都非常重视径向滑动轴承润滑性能的研究，随着相关仿真技术的进步，在求解方法[1-3]和边界条件[4-6]等方面，开展了大量广泛的工作，取得了很多实用性结果。在全周径向滑动轴承中，油膜几乎不可能是完整的，在旋转轴颈的驱动下润滑剂由轴承最大间隙流向最小间隙时，通过收敛的楔形空间，经过最小间隙后，轴颈与轴承之间的间隙空间开始增大，最小间隙处的油膜切向压力分量引起的有效附加流动有助于充满增大的间隙空间，待间隙继续增大，油膜压力减小导致切向压力分量减小，没有足够的润滑剂去填充继续增大的间隙空间，油膜将会破裂，也即出现空穴效应。

求解Reynolds方程是进行径向滑动轴承润滑分析的基础，边界条件确定是求解Reynolds方程的前提。关于边界条件，裘祖斡和张慧生[7]、温诗铸和黄平[8]详细描述了Reynolds边界条件和双Reynolds边界条件，使用中均采用负压置零的方法处理，没有考虑油膜空穴现象。OLSSON[9]提出了一种能针对空穴效应自动判定边界条件的Reynolds方程求解方法，这种方法应用于径向滑动轴承润滑分析的计算结果比较符合试验值。ELROD和ADAMS[10]提出Elrod算法，之后VIJAYARAGHAVAN和KEITH[11]、ZHANG[12]对Elrod算法进行了改进，采用数值方法求解油膜区和空穴区润滑方程的统一表达式，使质量守恒边界条件(JFO)更好地应用于润滑分析。苏荭等人[13]研究了油膜边界条件对滑动轴承润滑特性的影响，发现在一定转速和偏心率下，与Reynolds边界条件相比，质量守恒边界条件下轴承承载力增大了20%左右。

径向滑动轴承在不同工况下工作时，产生空穴效应的情况将随之变化，对轴承润滑性能的影响不容忽视。为了研究不同工况下空穴效应对径向滑动轴承润滑性能的影响，本文作者根据能自动确定动态边界的控制方程，求解完整油膜区和空穴区润滑模型的统一润滑方程，对比分析在不同工况下空穴效应对径向滑动轴承油膜压力分布、油膜承载力、端泄流量和摩擦功耗等润滑性能的影响。

1 数学模型

1.1 润滑方程

不可压缩流体完整油膜区Reynolds方程[14]为

(1)

式中：p为油膜压力；h为油膜厚度；R为轴承半径；u为轴颈表面线速度;η为润滑剂动力黏度；θ和y分别为轴承的周向和轴向坐标。

油膜在空穴区只有剪切流动，即空穴区的空穴压力为常数。根据质点运动方程、连续方程、牛顿黏性定律和N-S方程，推导出空穴区的Reynolds方程[16]为

(2)

为了简化求解方程、提高求解效率，引入新的变量φ(空穴区为油膜空穴度，油膜完整区为压力比)和开关函数g：

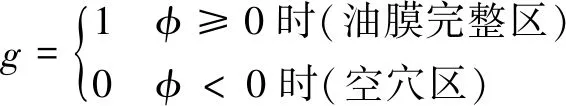
(3)

(4)

式中：ρ为润滑剂当量密度；ρc为润滑剂在空穴区的密度；ps为计算参考压力；pc为空穴压力。

根据变量φ和开关函数g得到能自动确定全周滑动轴承动态边界的统一控制方程为

(5)

根据式(1)、(2)和(5)可得完整油膜区和空穴区的统一润滑方程为

(6)

(7)

式中：L为轴承宽度；c为轴承半径间隙。

1.2 油膜厚度方程

h=c+ecos(θ-φ)

(8)

式中：φ为偏位角；e为偏心距。

1.3 轴承承载力

轴承承载力在坐标轴上的分量为

(9)

(10)

轴承承载力为

(11)

1.4 端泄流量

润滑剂单位时间内通过单位宽度截面的体积流量为

(12)

计及空穴效应时由于负压区的存在会导致润滑剂由轴承两端面向内流动，不考虑端部供油时，必须满足qy≥0，则轴承前端面和后端面的润滑剂流量分别为

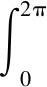
(13)

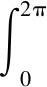
(14)

轴承润滑剂的总端泄流量为

Q=Q1+Q2

(15)

1.5 摩擦功耗

(16)

2 数值计算

2.1 求解方法

量纲一化润滑方程(7)采用有限差分法求解。图1给出了轴承内各节点控制体单元示意图，其中i和j分别代表轴承周向和轴向节点编号。为提高计算精度和保证单个节点单元网格接近于正方形提高准确度，求解域划分后的网格在轴承周向取m=360个节点，在轴向取n=70个节点。

图1 轴承节点单元示意图

将Reynolds方程和润滑方程的量纲一化形式(7)进行离散差分，方程左边用中心差分方法离散，方程右边采用迎风格式方法离散。完整差分形式为

(17)

离散润滑方程(17)采用超松弛迭代法(SOR)求解，轴承承载力、端泄流量和摩擦功耗公式中的积分应用Simpson公式进行数值积分，偏导数应用四点差分公式计算。

2.2 收敛准则

为了判断k次迭代结果是否达到足够精度从而决定是否终止迭代过程，需要确定收敛准则。收敛准则为

(18)

3 计算结果与分析

3.1 模型验证

油膜压力的分布情况是滑动轴承润滑性能最直接的体现。图2所示为在相同条件下，采用文中模型方法计算的轴承油膜压力与文献[16]试验数据的比

较，可见文中建立的控制方程和润滑统一方程与轴承实际情况较符合。

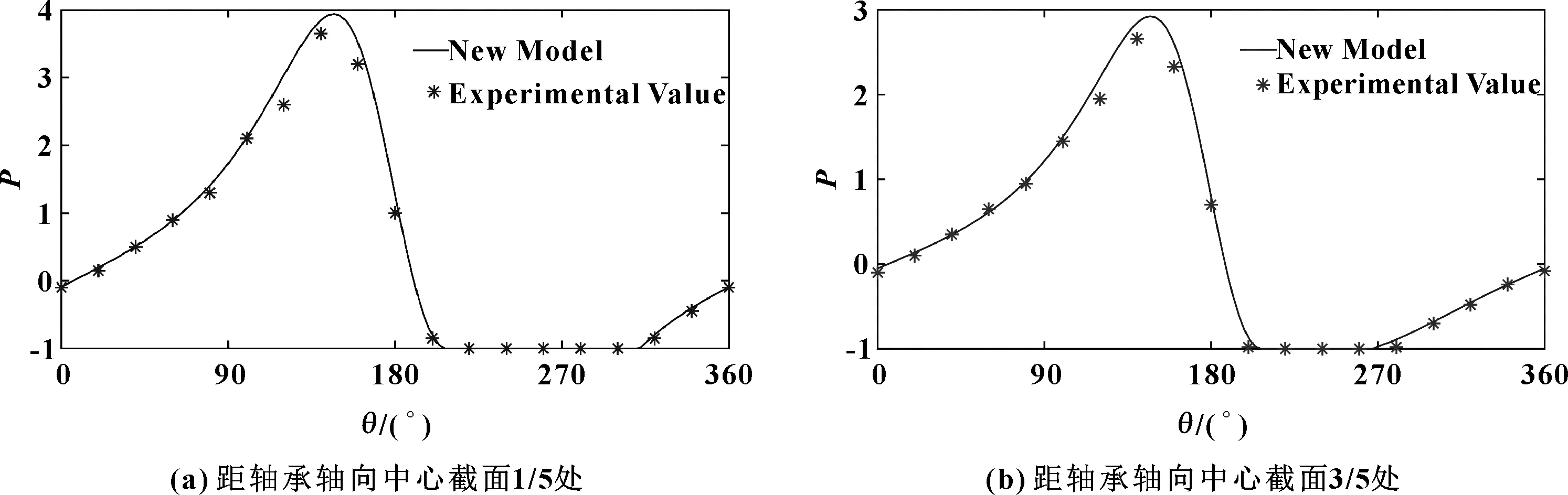
图2 轴承油膜压力计算值与试验值比较

3.2 结果与分析

文中以某燃油泵径向滑动轴承为对象，研究不同工况(转速和负荷)下空穴效应对轴承润滑性能的影响，其中负荷用偏心率表征。轴承工况和几何参数如表1所示。

表1 工况与几何参数

图3示出了转速5 000 r/min下，分别采用Reynolds边界条件和质量守恒边界条件(JFO)得到的不同偏心率下的轴承油膜压力云图。Reynolds边界条件下的轴承油膜压力只有正压区，而在相同偏心率和转速下，质量守恒边界条件下的轴承油膜压力一般包括正压区(PPZ)、负压区(NPZ)和负压区中的空穴区(CZ)3个区域。随着偏心率的增大，质量守恒边界条件下的轴承油膜压力的正压区明显增大，负压区明显减小；而空穴区在偏心率小于等于0.8时增大较明显，偏心率大于0.8后开始有减小的趋势。而Reynolds边界条件下轴承油膜压力只有正压区，且随着偏心率的增大有减小的趋势。当偏心率为0.2时，2种边界条件下轴承均不存在空穴区，产生这种情况的主要原因是偏心率较小时，轴承油膜压力小，轴承最小油膜厚度相对于最大油膜厚度变化较小，不具备形成空穴效应的条件。

图4所示为偏心率为0.6时，质量守恒边界条件下不同转速下的油膜压力分布。可知，偏心率相同时，质量守恒边界条件下轴承油膜压力的正压区随着转速的增加而减小，负压区和空穴区均随着转速的增加而增大，当转速达到一定值时，空穴区轴向宽度可能出现等于轴承宽度的情况，导致润滑剂在轴承中出现整体破裂。

图5示出了偏心率为0.9，转速分别为2 000和14 000 r/min时，2种边界条件下轴承中央截面的油膜压力分布情况。可知，与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，当油膜压力大于0时，轴承油膜压力分布相差很小；当油膜压力小于0时，轴承油膜压力的分布相差较明显，这说明空穴效应的影响较明显；转速为2 000 r/min时，Reynolds边界条件下轴承油膜的正压区约为192°，其余为0；质量守恒边界条件下轴承油膜的正压区约有234°，负压区约为126°，空穴区约为87°，与Reynolds边界条件下的结果相比较，油膜正压区增大了21.9%。

图3 5 000 r/min时不同偏心率的轴承油膜压力区域分布(左图为质量守恒边界条件结果，右图为Reynolds边界条件结果)

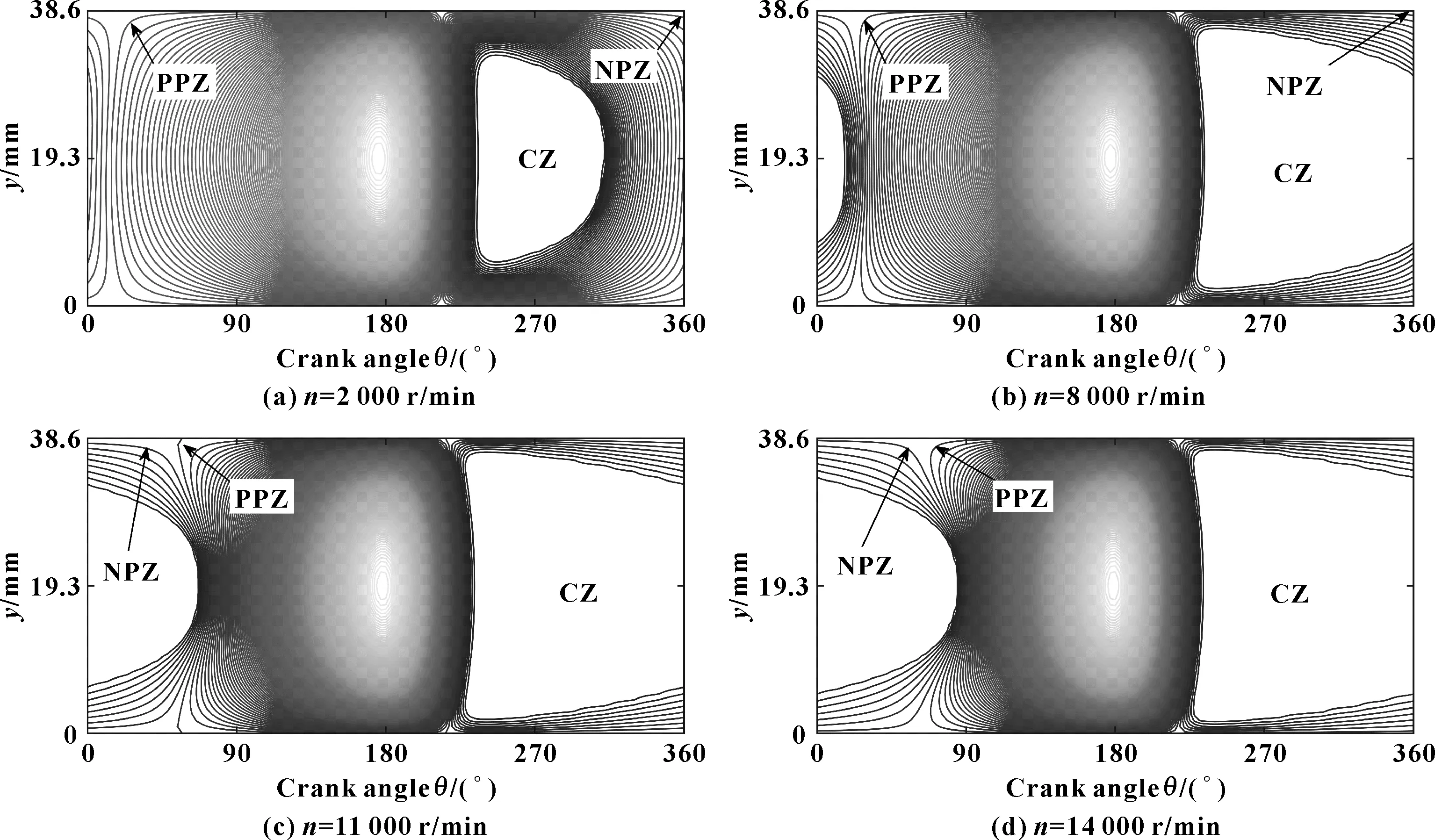
图4 不同转速下的轴承油膜压力区域分布(ε=0.6)

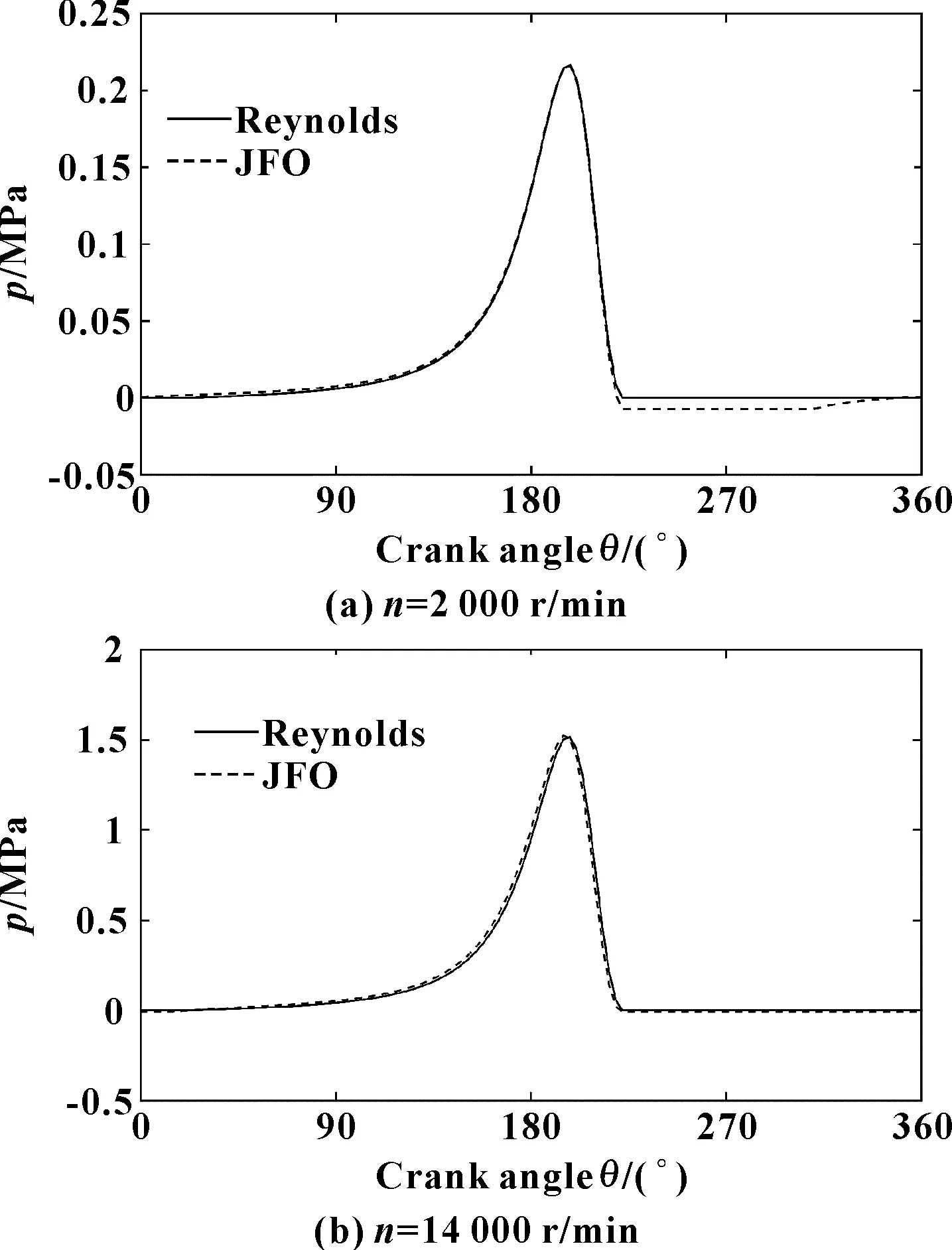
图5 不同边界条件下轴承中央截面油膜压力分布(ε=0.9)

图6示出了不同边界条件下轴承承载力随转速和偏心率的变化。可知，当偏心率较小(ε=0.2)时，随转速增加，与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，轴承承载力有所增加，转速较高时增加较多；当偏心率很大(ε=0.98)时，随转速增加，与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，轴承承载力略有减小。

图6 不同转速和边界条件下轴承承载力随偏心率的变化

表2给出不同工况下，2种边界条件下的燃油泵径向滑动轴承的承载力。可见，转速相同时，在一定的偏心率下，与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，轴承承载力一般呈现增加的变化趋势；但是当偏心率大于等于0.95时，轴承承载力会出现减小现象，主要原因是空穴效应随着偏心率增加产生的影响越加明显，较大的负压区和空穴区导致的完整油膜整体破裂，从而降低轴承承载力。

表2 不同边界条件和偏心率下的轴承承载力

图7示出了不同边界条件下轴承端泄流量随转速和偏心率的变化。可知，与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，不同转速时润滑剂端泄流量随着偏心率的增大明显减小，当偏心率很大(ε=0.98)时，轴承端泄流量又有明显增大；与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，不同偏心率时润滑剂端泄流量随转速的增大减小更明显，当偏心率很大(ε=0.98)时，轴承端泄流量或出现突然增大现象。转速为14 000 r/min、偏心率为0.4时轴承的端泄流量降低了38.8%；转速为11 000 r/min、偏心率为0.98时轴承的端泄流量增大了43.9%，出现这种现象的主要原因是空穴效应使油膜出现较大的负压区，使一部分润滑剂在压力梯度的影响下出现内部流动，故轴承端泄流量减小，但是当偏心率达到一定值时，油膜中的空穴区大大增加，空穴效应可能导致油膜在轴承的周向出现整体破裂的现象，导致轴承端泄流量明显增加。

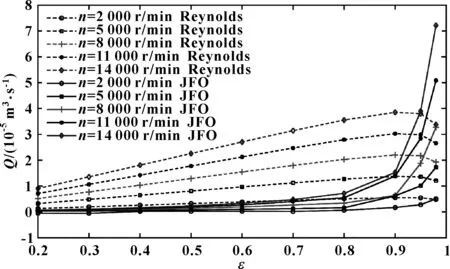
图7 不同转速和边界条件下轴承端泄流量随偏心率变化

图8示出了不同边界条件下轴承摩擦功耗随转速和偏心率的变化。可知，与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，相同转速时轴承的摩擦功耗略有增加。

图8 不同边界条件下轴承摩擦功耗随偏心率的变化

表3给出不同工况下，2种边界条件下燃油泵滑动轴承的摩擦功耗。转速相同时，在一定的偏心率下，与Reynolds边界条件下的结果相比较，在质量守恒边界条件下，轴承摩擦功耗均略有增加。

表3 不同边界条件和偏心率的轴承摩擦功耗

4 结论

(1)不同工况(转速和负荷)下，与Reynolds边界条件比较，在质量守恒边界条件下，径向滑动轴承的油膜压力存在区域和分布情况有较明显不同；偏心率相同时，随转速的增加，油膜负压区和空穴区明显增大；转速相同时，随偏心率的增加，油膜正压区明显增大，负压区明显减小，空穴区一般呈现增大变化趋势，但是当偏心率增加到一定值时(ε>0.95)可能出现减小现象。

(2)不同工况下，与Reynolds边界条件比较，在质量守恒边界条件下，转速相同，偏心率较小时，轴承承载力一般有一定增加；偏心率大于等于0.95时，急剧增大的空穴区使轴承承载力出现减小现象。

(3)不同工况下，与Reynolds边界条件比较，在质量守恒边界条件下，轴承端泄流量有明显变化。转速相同、偏心率较小时，空穴效应产生的负压区使轴承端泄流量回流而明显减小，偏心率增大到一定值后剧烈的空穴效应会导致轴承端泄流量突然增大。

(4)不同工况下，与Reynolds边界条件比较，在质量守恒边界条件下，负压区的存在使轴承摩擦功耗略有增加。