一种考虑波动效应的拟动力地震边坡稳定性分析方法

邓亚虹，徐 召，孙 科，2，闫佐菲

(1. 长安大学 地质工程与测绘学院，陕西 西安 710054； 2. 中国煤炭地质总局航测遥感局，陕西 西安 710199)

0 引 言

边坡稳定性与人类生产、生活密切相关，边坡失稳常造成巨大的生命、财产损失，而地震是诱发边坡失稳的最主要因素之一。1964年阿拉斯加地震中，由边坡失稳引起的损失和伤亡占56%[1]。2008年汶川地震引发了数以万计的滑坡，死亡人数超过1 000人的滑坡就有30 余个[2]，滑坡还破坏了大量生命交通线，严重阻碍救援工作[3]。中国是一个多山国家，存在大量人造边坡和自然斜坡。同时，中国地处环太平洋地震带与欧亚地震带之间，地震断裂带发育。因此，地震边坡稳定性分析直接关系到中国的国计民生。

目前，地震边坡稳定性分析方法以拟静力法为主，因其计算简便、实用性较强，被纳入许多规范[4-7]。拟静力法源于地震工程结构的地震反应分析[8]，后由Terzaghi引入地震边坡稳定性分析[9]，将地震力简化为恒定的惯性力施加到边坡坡体。早期的拟静力法仅考虑水平地震力，Chopra等证明了竖直地震力对地震边坡稳定性的影响不可忽略[10-11]。后续，拟静力法得到进一步完善：Biondi等基于拟静力法研究了孔隙水压力对地震和地震后无限饱和黏土边坡稳定性影响，并提出了边坡稳定系数的计算公式[12]；Baker等采用拟静力法对边坡进行地震稳定性分析，提出一个适用于大部分均质边坡的拟静力分析设计图表[13]。不过，拟静力法还存在许多问题：地震系数取值尚未有直接有效的确定方法[14-15]；刚性坡体假设是不准确的；基于传统竖向条分的拟静力法在计算地震力和抗滑弯矩时存在误差[16]；拟静力法未考虑地震动特性等。这些因素都导致拟静力法计算结果过于粗略。

针对拟静力法存在的不足，Steedman等提出拟动力法[17]；尔后，Choudhury等完善了拟动力法及其速度公式[18-20]，并将该方法引入地震边坡稳定性分析，对一处尾矿坝进行了稳定性分析[21]；Choudhury等还考虑了地震放大效应之后，对拟动力法进行了改进[22]。Chakraborty等还分别采用传统的拟静力法和拟动力法，对位于印度东部的44 m高保水型尾矿坝进行了地震边坡稳定性分析，结果也清楚地表明了常规拟静力法的局限性[23]。后续，多位学者对边坡的地震响应进行探究[24-25]，为拟动力法发展提供了理论支撑。此外，Nimbalkar等分别研究了高卓越频率和低卓越频率地震作用下边坡稳定性安全系数的变化规律[26]；Hou等也探讨了不同地震系数和卓越频率下安全系数的变化趋势[27]。

拟动力法用于地震边坡稳定性分析起步较晚，当前研究也仅限于单个地震动参数对安全系数的影响，并未从本质揭示拟动力法用于地震边坡稳定性分析的优势，也尚未形成科学、简便、适用于工程实践的方法。现行规范在设计理论和工程实践上仍然处于粗浅的经验阶段，急需借鉴地震工程的新理论、新方法来推动地震边坡稳定性分析的现代化和规范化[28]。因此，开展拟动力地震边坡稳定性分析方法研究具有重大的理论和实践意义[29-31]。

本文基于拟动力法，结合传统静力边坡稳定性分析极限平衡法(瑞典条分法)，推导了边坡地震力公式和地震边坡稳定性安全系数公式，借助MATLAB软件开发了最危险滑面搜索和安全系数求解程序，实现了一种考虑波动效应的拟动力地震边坡稳定性分析方法，并从波动理论角度揭示了拟动力法与拟静力法的区别与联系。

1 基本原理

图1 拟动力法原理Fig.1 Principle of Pseduo-dynamic Method

拟动力法最初用于挡土墙土压力计算，它假设地震波为从基底垂直入射的正弦波(图1)。从图1可以看出高度为H，滑面倾角为α的挡土墙结构。土体和土体与墙体摩擦角分别为φ和δ，土体重力为W，坡体对滑体的支持力为F，水平地震力为Qh，主动土压力为Pae。

t时刻，z深度处长度为dz的土体所受水平加速度(ah(z,t))为

(1)

式中：ah为拟静力水平加速度；ω为横波圆频率；vs为横波波速。

Choudhury等同时考虑水平和竖直地震力作用，对拟动力法进行了完善[18-20]。此后，阮晓波等假设地震加速度幅值由坡底到坡顶线性增加，给出了考虑地震放大效应的拟动力加速度[21]，其表达式为

(2)

式中：av(z，t)为t时刻，z深度处长度为dz的土体所受竖直加速度；av为拟静力竖直加速度；vp为纵波波速；fs为地震放大系数。

类似于挡土墙土压力计算，Choudhury等在对尾矿坝进行地震边坡稳定性分析时，采用拟动力法计算地震力[22]。不考虑地震放大系数，假设滑面为圆弧形。如图2所示，均质尾矿坝高为H，坡角为β，圆弧半径为R，同时受水平和竖直地震力作用(水平和竖直加速度无相位差时为最危险地震荷载组合)。取深度为z的条块，条块底面倾角为θ，水平和竖直地震力臂分别为XNS，O和YNS，O。

图2 尾矿坝拟动力分析Fig.2 Pseudo-dynamic Analysis of Tailing Dam

2 基于拟动力法的瑞典条分法

Choudhury等在进行尾矿坝地震边坡稳定性分析时采用水平条分法，并对条间力进行了假设[22]。但是，这些条间力假设过于复杂，其合理性还有待检验，加之安全系数计算过程也比较繁琐，不便用于工程应用。相比较而言，传统竖向条分法发展成熟，条间力假设简单实用，已被广泛理解和接受。本文将基于拟动力法和极限平衡法(瑞典条分法)推导边坡地震力公式及安全系数公式。

2.1 地震力公式

本文选用的拟动力公式未考虑地震放大效应，一方面因为现有的研究成果都是建立在各种假设的基础上，并不能反映真实的放大效应，另一方面因为本文的主要目的是探究波动效应及其影响规律。

在t时刻，位于深度z处，长度为dz，宽度为b，密度为ρ的块体所受水平地震力(Fh)和竖直地震力(Fv)计算公式为

(3)

其中，拟静力水平加速度ah=khg，拟静力竖直加速度为av=kvg，其中，kh为水平地震系数，kv为竖直地震系数，g为标准重力加速度。圆频率ω=2πf，f为卓越频率。

如图3所示，对潜在滑体竖向分条，在t时刻，取位于深度z处的第i个条块，其长度和宽度分别为zi和bi，则整个条块所受地震力可由积分得到

(4)

式中：Fhi和Fvi分别为条块i所受的水平地震力及竖直地震力；fh和fv分别为横波和纵波卓越频率。

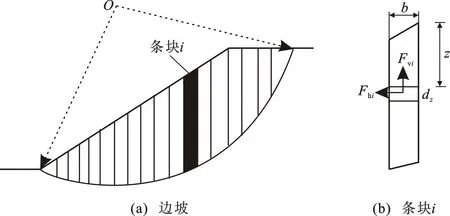
图3 地震力求解示意图Fig.3 Schematic Diagram of Seismic Force Solution

2.2 安全系数公式

地震边坡稳定性安全系数公式推导选用瑞典条分法。瑞典条分法是最基础的条分法，其假定条间力对边坡整体稳定性影响可忽略[32-33]，假设简单，能够排除条间力的各种耦合作用对地震力的影响，便于直观展示采用拟动力法进行地震力计算带来的影响，从而揭示波动效应在地震边坡稳定性分析中的重要性。

对滑体进行竖向分条，根据极限平衡理论有径向力平衡，则

Ni=Wicosθi-Fhisinθi-Fvicosθi

(5)

根据滑面上极限平衡条件，则

(6)

考虑滑体整体力矩平衡条件，则

∑Wicosθi+∑Fhicosθi=∑Ti+∑Fvisinθi

(7)

式中:Ni为条块i所受支持力；Wi为条块i所受重力;Ti为条块i所受剪力；Tfi为土体的抗剪强度；ci为土体黏聚力；li为条块i滑面长度；θi为条块i滑面倾角；φi为条块i土体摩擦角；Fs为安全系数。

将式(5)和式(6)代入式(7)，整理后得

Fs=[(∑Wmicosθi-∑Fhisinθi-

∑Fvicosθi)tanφi+∑cili]/

(∑Wisinθi+Fhicosθi-∑Fvisinθi)

(8)

式(8)即为基于拟动力法和瑞典条分法的地震边坡稳定性安全系数公式。需要说明的是，在推导过程中，为保持与瑞典条分法假设的一致性，未考虑单个条块是否满足静力平衡。上述推导中，地震力作用位置选取为条块底部，有以下两方面原因。

(1)拟动力法假设地震波为正弦波，所求得的地震力不是均匀分布的，而是随波形变化的，而且不同条块波形分布不同，因此，不同条块地震力作用点也不同。在地震边坡稳定性分析过程中，要对最危险滑面进行搜索，而此搜索过程是在地震力作用点确定情况下进行的。若想要确定不同条块的地震力作用位置，需先选定作用位置，通过滑面搜索结果验证选取位置是否准确，这是一个迭代逼近的过程。但是，这个过程过于繁冗，不利于理论和规律研究，因此，本文将地震力作用位置简化为条块底部是比较合理的选择。

(2)从数学角度分析，地震力作用位置影响的是安全系数公式中的力矩，但是安全系数分子、分母均包含这个力矩，所以力矩的变化对安全系数影响不大。通过实际验证地震力作用点分别选为条块重心或者条块底部，结果表明安全系数差异不大。本文研究的核心内容为拟动力法和地震波动效应，地震边坡稳定性分析方法为这二者依托的载体，安全系数为这二者的表现形式，地震力作用位置选为条块底部能够满足研究需求且有其合理性。后续可讨论不同方法和地震力作用位置对精度的影响。

3 MATLAB程序实现及验证

借助MATLAB软件编制了计算程序，实现了拟动力法地震力计算和最危险滑面的搜索，最终得到地震边坡稳定性安全系数。

为检验MATLAB算法的有效性，首先试算静力和拟静力安全系数，并与理正岩土软件所得安全系数进行对比。算例边坡模型如图4所示，试算边坡的几何特征参数、物理力学指标及计算结果汇总于表1。由表1可知，MATLAB程序所得结果与理正岩土软件计算结果基本一致，验证了MATLAB程序的有效性。

图4 边坡模型Fig.4 Slope Model

4 基于拟动力法的地震边坡稳定性

4.1 算例分析

本部分计算仅考虑水平地震力，沿用图4的边坡模型，具体参数如表2所示。其中，物理力学指标取自多组黄土物性指标试验中位数，地震卓越频率取自统计分析多条地震动记录结果的中位数[34]，横波波速取自《建筑抗震设计规范》(GB 50011—2010)[35]中给出的黄土横波波速中位数。

分别采用拟静力法和本文选用的拟动力法对算例边坡进行稳定性分析，拟静力法得到的安全系数为0.962，拟动力法得到的安全系数为0.997，后者明显大于前者，这与Choudhury等的研究结果[22]是一致的。

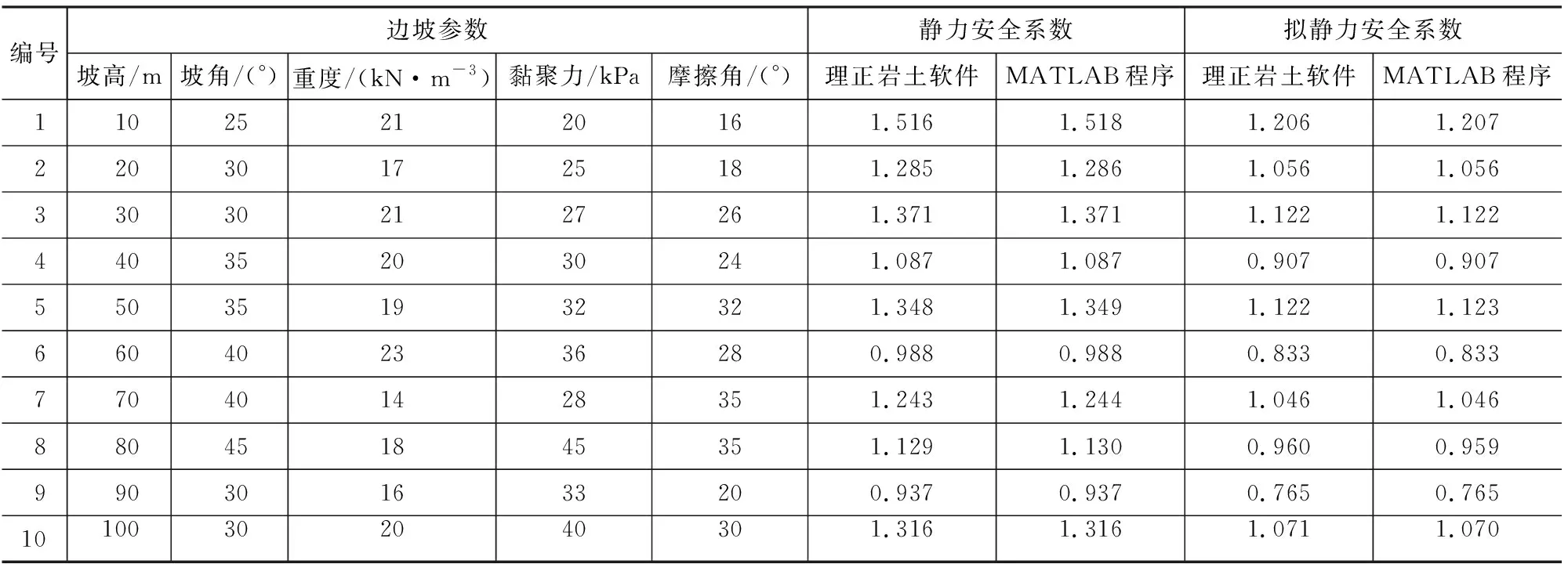
表1 MATLAB程序边坡实例试算参数

表2 算例边坡参数

4.2 波动效应对地震边坡稳定性影响

拟动力法考虑了地震波动效应，所得的安全系数更契合实际，本文将具体分析波动效应对地震边坡稳定性的影响。地震波动效应主要由地震动特性和坡体材料特性决定，下面分别讨论地震波初始相位、地震动幅值、地震卓越频率和波速对地震边坡稳定性的影响，进而揭示波动效应对地震边坡稳定性的影响。

4.2.1 初始相位

Choudhury等的研究中并未探究地震波初始相位对安全系数的影响[22]，而实际上地震波初始相位应为最危险初始相位，对应最危险工况(安全系数即为最小安全系数)。改变算例边坡初始相位，绘制安全系数随初始相位变化趋势(图5)。由图5可知，安全系数随初始相位周期性波动，最大值为1.176，最小值为0.997。其中，最小值即为地震边坡稳定性安全系数。

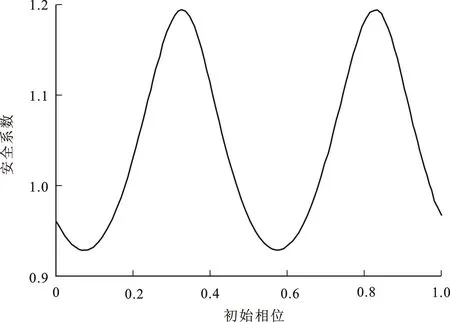
图5 安全系数随初始相位变化趋势Fig.5 Variation Trend of Safety Factor with Initial Phase

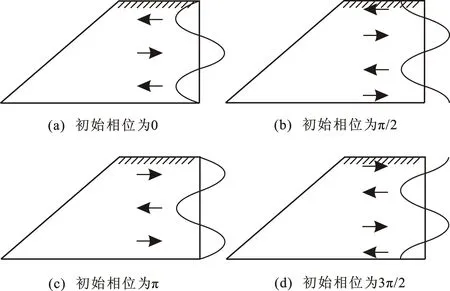
图6 坡体内不同初始相位波形Fig.6 Different Initial Phase Waveforms in Slopes

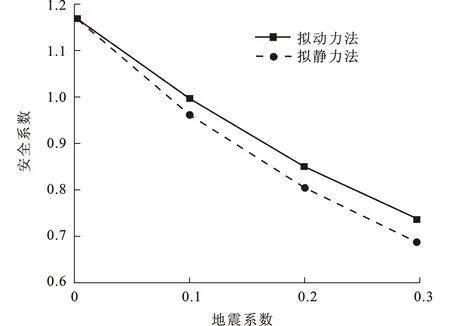
图7 安全系数随地震系数变化趋势Fig.7 Variation Trend of Safety Factor with Seismic Coefficient

安全系数随初始相位波动变化由地震的波动效应造成。如图6所示，拟动力法假定地震波为正弦波，不同初始相位会使坡体受到大小、方向不同的地震力，安全系数自然也随地震力同步变化。

4.2.2 地震动幅值

由拟动力法地震力公式可以看出，地震动幅值受地震系数选取的影响。关于地震系数的选取，目前尚未有直接快速方法，这里对此不进行探讨。改变上述算例中的地震系数，分别运用拟动力法和拟静力法进行计算，结果如图7所示。由图7可知，拟动力法所得安全系数大于拟静力法，且随地震动幅值(或地震系数)的增大，差值逐渐增大。Choudhury等分别探究了地震系数对安全系数的影响[22,27]，结果与本文是一致的。

如图8所示，拟动力法假设地震波为从基底垂直入射的正弦波，坡体内质点加速度方向大小都不同；而拟静力法假设坡体内各质点加速度相同，这就导致拟动力地震力比拟静力地震力小，这也是拟静力法过于保守的根本原因。而随地震力增大，这种现象会更加明显，拟动力法与拟静力法所得结果差距增大。

图8 拟静力和拟动力地震力示意图Fig.8 Seismic Force Diagrams of Pseudo-static and Pseudo-dynamic Methods

4.2.3 卓越频率和波速

卓越频率(f)和波速(v)对拟动力安全系数的影响实际上是地震波波长(λ)对安全系数影响的两种表现形式。波长、卓越频率和波速的关系为

λ=v/f

(9)

对于给定的波速，波长与卓越频率呈反比；对于给定的卓越频率，波长与波速成正比。

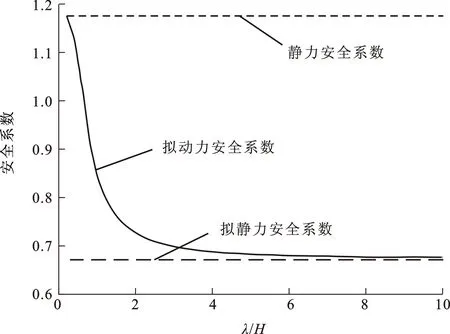
图9 安全系数随λ/H值变化趋势Fig.9 Variation Trend of Safety Coefficient with λ/H

地震波波长对拟动力安全系数的影响由地震波波长与边坡坡高比(λ/H)决定。由安全系数随λ/H值变化趋势(图9)可以看出：当λ/H值高于10时，拟静力法与拟动力法算得的安全系数基本一致；当λ/H值低于10时，拟动力法算得的安全系数要大于拟静力法。工程实践中，边坡坡高一般为10～100 m，坡体材料波速一般为100～500 m·s-1，而地震动频率一般为0.5～7.0 Hz，则常见λ/H值最小为0.15，且有相当一部分边坡的λ/H值为0.15～10.00。因此，本文所做工作是有必要的。当然对于不同坡角和滑面类型的边坡，λ/H值可能存在一定差异，但拟静力法计算与拟动力法计算结果差异规律与图10一致。

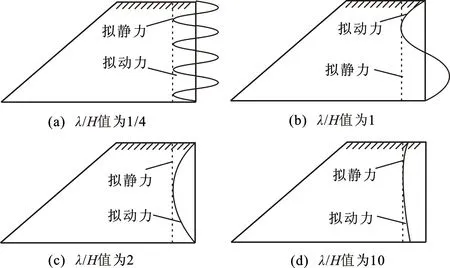
图10 不同λ/H值下拟动力、拟静力地震力示意图Fig.10 Seismic Force Diagrams of Pseudo-static and Pseudo-dynamic Under Different λ/H

Choudhury等的研究中讨论了正弦波周期对安全系数的影响[22]，Hou等也进行了类似的讨论[27]，结果都表明随正弦波周期增大(或卓越频率减小)，安全系数减小，这与上述规律也是一致的。

如图10所示，从波动理论出发，当λ很小(f很大或v很小)，即λ/H值很小[图10(a)]时，整个坡体跨越多个波长，坡体所受的正、反向地震力近似抵消，与静力状态基本一致，拟动力安全系数也就十分接近静力安全系数；随λ/H值增大[图10(b)、(c)]，坡体跨越波长范围减小，拟动力安全系数逐渐减小；当λ很大(f很小或v很大)，即λ/H值很大[图10(d)]时，整个坡体仅跨越波长的一小段，坡体内质点加速度近似相同，与拟静力法假设基本一致，拟动力安全系数也就十分接近拟静力安全系数。

5 结 语

(1)本文考虑地震波动效应，基于拟动力法，结合极限平衡法推导了边坡地震力公式和地震边坡稳定性安全系数公式，并借助MATLAB程序实现了地震边坡稳定性安全系数的计算。从波动理论出发，讨论了地震动特性对地震边坡稳定性安全系数的影响，揭示了拟动力法与拟静力法本质区别，并指出当地震动波长与边坡坡高比小于10时，地震波动效应明显，地震边坡稳定性分析采用拟动力法更为合理。

(2)本文研究对象为均质边体，未考虑边坡几何特征、坡体材料和地层等因素的影响以及拟动力法与拟静力法最危险滑面之间的差异，后续还需进一步研究。此外，仅选取了瑞典条分法进行拟动力法与拟静力法之间的对比，关于其他各类条分法还有待继续探究。