粗砂滑坡离心模型试验及离散元细观模拟
杜强, 曲立强, 刘俊芳,2*
(1.内蒙古工业大学土木工程学院, 呼和浩特 010051; 2.沙旱区地质灾害与岩土工程防御自治区 高等学校重点实验室, 呼和浩特 010051; 3.同济大学地下建筑与工程系, 上海 200092)
近年来,中国部分地区暴雨频发,引发了众多地质灾害,滑坡是常见的地质灾害之一,滑坡灾害会对周边人民生命财产造成严重损失,降雨是导致滑坡的重要因素[1]。然而降雨诱发滑坡的形成机理和力学过程比较复杂,迄今仍是尚未取得共识的前沿课题。
中外学者针对降雨诱发滑坡进行了一系列研究,取得了许多成果,如朱谭方等[2]、胡航[3]、 Liang等[4]分别对硬土软岩、松散堆积土体和膨胀土边坡进行了滑坡启动机理的研究;孙立娟等[5]、 Jiang等[6]探索了库水复活型滑坡的破坏模式与力学机制;耿正等[7]研究了前缘反倾式锁固型滑坡在不同坡面形态时的变形破坏状态等;但在研究方法上存在诸多差异,其中,离心模型试验具有能近似模拟原型重力场应力条件、可以再现自重应力场及与自重有关的变形过程、可以直观揭示变形破坏机理等优点在滑坡机理研究方面得到广泛的应用。薛德敏[8]、钱纪芸等[9]通过离心模型试验,研究了边坡的渐进破坏机理、变形和破坏特性等问题;詹良通等[10]利用离心模型试验,对雨强—历时警戒曲线进行了验证;王维早等[11]]通过离心模型试验,研究了强降雨诱发沿基覆界面滑动的浅表层堆积层滑动形成机制;杜强等[12]和周健等[13]利用自主研发的可视化离心机模型试验装置对无黏性土滑坡型泥石流的形成机理进行了研究。上述研究大多是从宏观的角度对离心模型试验中的滑坡过程进行研究,然而滑坡是一个动态过程,存在岩土体的滑动、平移、转动和土体的断裂及松散等复杂过程,具有宏观上的不连续性和单个土体运动的随机性。因此,从土体细观尺度层面入手探索颗粒运动与宏观力学特性之间的内在关联对于研究滑坡有重要意义。同时,在目前针对滑坡机理研究方面的数值模拟方法中,离散单元法克服了传统连续介质力学模型的宏观连续性假设,在获得土体宏观力学响应的同时,也可以从细观的角度去模拟土体的力学特性,并能获得任意时刻试样细观组构的空间分布状况及其相关的统计信息,通过对土体颗粒结构的细观参数的研究来分析和解释其宏观力学响应。从细观和非连续角度研究滑坡形成机理,将有助于揭示滑坡的力学机理,基于滑坡的离心模型试验,针对试验所得数据,开展相应的数值模拟分析和验证十分必要。
不少学者采用离散元方法对滑坡进行了研究。李龙起等[14]通过PFC2D数值模拟软件引入接触黏结模型模拟降雨诱发边坡破坏过程特征;戴健健等[15]利用PFC2D标定了土体的细观参数并建立了边坡颗粒流模型,对位移突变准则进行了改进;Va-lentino等[16]通过室内小模型试验和离散元法相结合的方法,对斜面上干砂颗粒的流动进行分析,在试验过程中通过设置特征颗粒观察颗粒的流动现象和破坏特征,数值模拟结果与试验现象一致,并指出采用颗粒流程序对模拟滑坡的可行性,缺点是数值模拟中只考虑颗粒间的相互作用,忽略了水体的作用;马秋娟等[17]利用自制模型槽结构,结合PFC2D数值模拟软件,对坡度为25°固定单宽流量下滑坡启动过程进行了试验和数值模拟;李世俊等[18]利用离心模型试验和数值模拟相结合的方法研究了采空条件下边坡的渐进破坏过程及破坏模式;周健等[19]采用PFC3D对滑坡型泥石流启动过程的模型试验进行数值模拟研究。以上研究,基于数值模拟成果,研究试样宏观力学性质和细观参数的演化规律,从细观角度对土体滑坡的演化机理进行阐述,但未考虑滑坡过程中土-水相互作用问题和滑坡前坡体的非饱和特性。
鉴于此,现利用自行研制的降雨诱发滑坡离心模型试验装置进行离心模型试验,在接近实际应力条件下分析粗砂坡体滑坡的宏细观力学特性及演化规律,同时考虑滑坡发生前土体的非饱和特性,对PFC3D的模拟方法进行改进,并用改进后的方法对粗砂滑坡形成过程进行数值模拟,从细观角度对离心模型试验进行补充。
1 离心模型试验
利用同济大学土工离心机进行降雨诱发粗砂滑坡的离心模型试验,离心模型试验系统如图1所示。
离心模型的比尺为20,离心加速度为20g(g为重加速度)。在制备模型时模型的物理量严格按照相应的比尺进行设计,另外,模型试验是完全理想状态,而实际边坡不论从边界条件、土体性质方面均与模型试验存在一定的差异。离心机内采用90 cm×70 cm×70 cm且一侧透明的模型箱,在模型箱内放置模型槽,模型槽宽度为25 cm,深度为20 cm。试验过程中通过调整空气压缩机的不同气压值来控制降雨强度。
为节省时间和获得更好试验破坏效果,采用0.005~0.10 mm的石英粉作为试验土样模拟粗砂,模拟粗砂的颗粒级配曲线如图2所示。
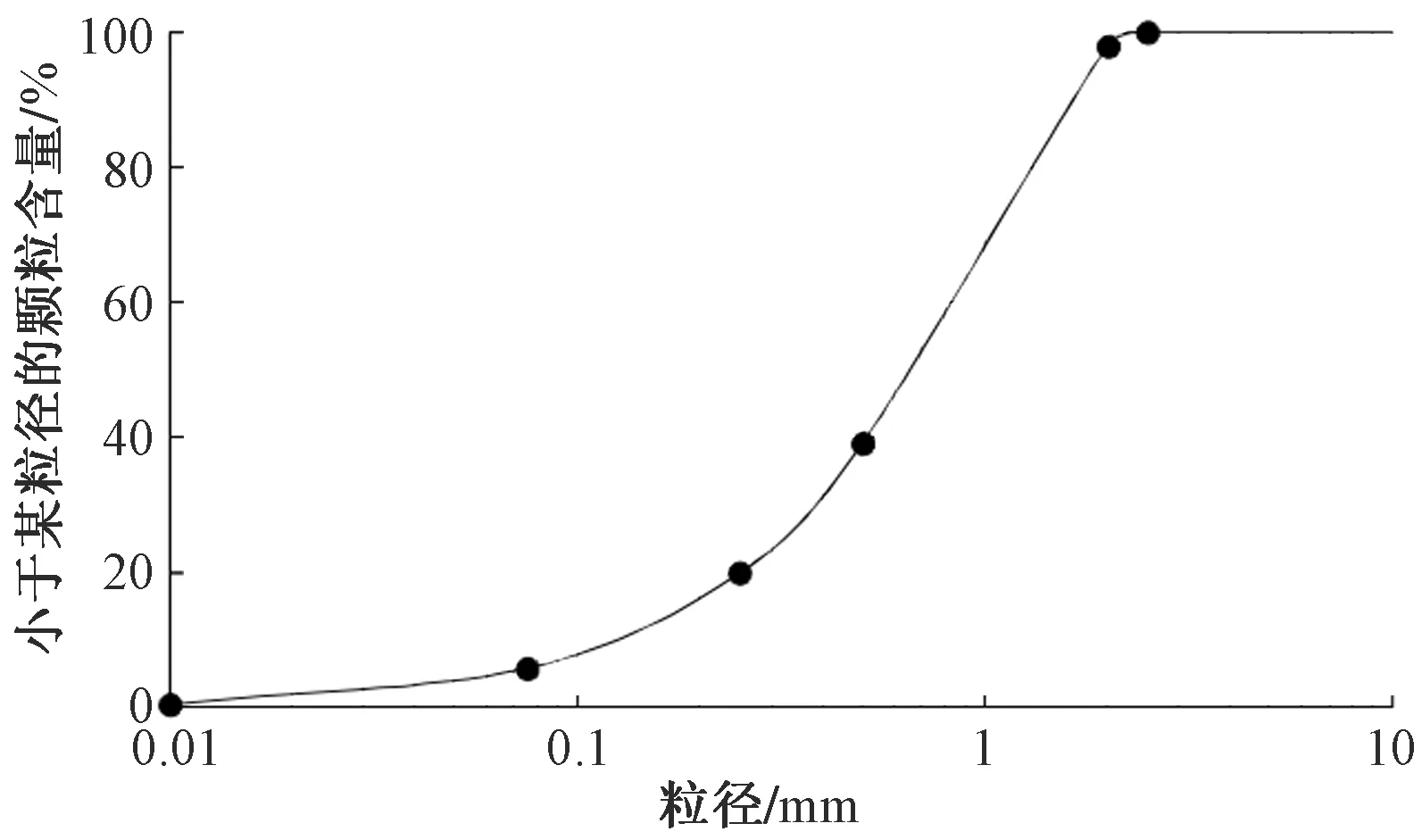
图2 模拟粗砂的颗粒级配曲线Fig.2 Particle size distribution curve of simulated coarse sand
选取降雨强度36、43、50、56 mm/h共进行了4组离心机模型试验,试验编号分别为LX-1、LX-2、LX-3、LX-4。图3为不同降雨强度下模拟粗砂坡体滑坡的破坏模式。

图3 坡体破坏模式Fig.3 Failure mode of slope
由图3可以看出,在降雨强度36~50 mm/h的条件下,坡体表面产生明显的下沉,当降雨进行到一定时间时,坡体后部土体突然启动,并推动前部土体整体流滑,滑动的土体在降雨的作用下,迅速发生滑动。滑坡形成突然,破坏规模大,滑动速度快。在降雨强度56 mm/h下,坡体没有发生明显的沉降,降雨快速入渗后,坡体整体在某一时刻直接流态化,以黏稠状水土混合物的形态快速向下流动。
2 数值模拟方法的改进
为了进一步从细观方面对滑坡形成过程及机理进行研究,利用三维颗粒流程序(PFC3D)建立数值模拟模型,模拟滑坡的形成过程,分析颗粒位移矢量、速度矢量、颗粒接触力的变化以及水土相互作用规律,从细观角度研究由降雨诱发的滑坡现象,对离心模型试验结果进行补充。
采用微小颗粒类液态法[18]进行建模,在前期模拟室内模型试验的基础上对离心模型试验进行数值模拟。由于离心比尺效应,进行模拟时需要将土颗粒的粒径缩小,但考虑到计算机的计算能力,以及水颗粒的模拟,土颗粒的粒径无法与离心模型试验时相同,即将原型土体的粒径缩小20倍。采用两种方法解决上述问题。一种方法是采用与原型土体相同的颗粒粒径,通过对水颗粒施加一定的黏滞系数来近似模拟(下文简称大颗粒方法);另一种方法是将原型土颗粒体积缩小20倍来近似模拟(下文简称小颗粒方法)。
离心模型试验数值模拟的模型槽由四面刚性墙组成,其中一级坡体30°、底面长度50 cm,二级坡体10°、底面长度21 cm,底板与土颗粒设置相同的摩擦系数,取值0.6;其他三面(前、后、右)墙体代表试验中的玻璃侧壁和后壁,墙体高度0.3 m,摩擦系数取值为0,忽略墙体对颗粒运动的影响,墙体的细观参数取值如表1所示,在模型槽的左下侧没有墙体的存在,以便颗粒可以从该处自由滑落。坡体坡面的长度60 cm,坡体高度0.1 m,模型槽宽度25 cm。采用大颗粒方法时,颗粒粒径范围5.0~10.0 mm,水颗粒为 0.3~0.6 mm,重力加速度为20g,土颗粒间的接触模型采用接触黏结模型和滑移模型,并对水颗粒设置黏滞系数,颗粒的细观参数如表1所示。
采用小颗粒方法时,颗粒体积在模拟室内模型试验的基础上缩小20倍,土颗粒粒径范围1.84~3.68 mm,水颗粒为0.1~0.2 mm,重力加速度为20g,颗粒间的接触模型采用接触黏结模型和滑移模型,颗粒的细观参数如表2所示。
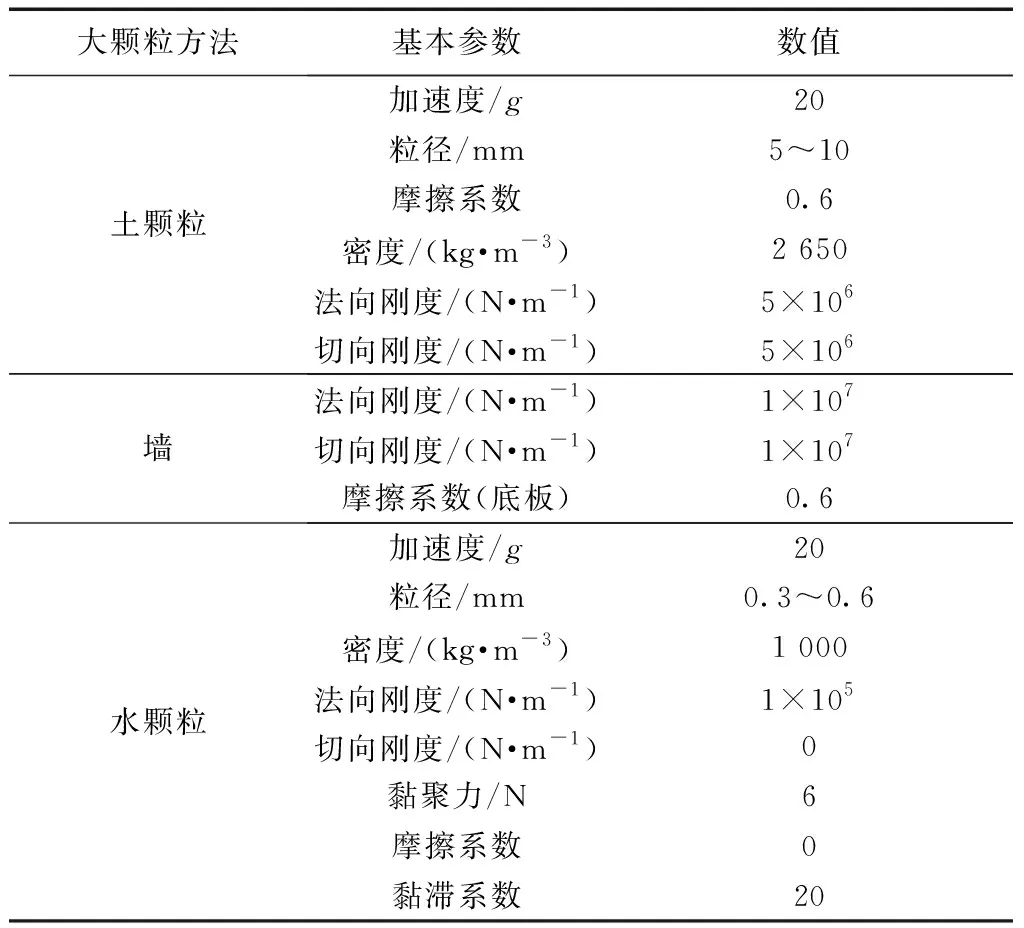
表1 大颗粒方法滑坡数值模拟细观参数Table 1 Meso-parameters for numerical simulation of landslides by large particle method
离心模型试验的数值模拟模型图如图4所示。与离心模型试验降雨条件相同,水颗粒只生成在一级坡体上的坡体内部,二级坡体内没有水颗粒。

表2 小颗粒方法滑坡数值模拟细观参数Table 2 Mesoparameters for numerical simulation of landslide by small particle method

图4 数值模拟模型图Fig.4 Numerical simulation model diagram
3 数值模拟结果与细观分析
对降雨诱发滑坡离心模型试验进行数值模拟,数值模拟试验现象与离心模型试验现象基本一致,图5为采用大颗粒方法对离心模型试验进行模拟的数值模拟和离心模型试验现象对比图。
从图5中可以看出:在试验初期,水颗粒均匀分布在坡体内部且以向下运动为主,导致坡体产生沉降现象。随着试验的进行,水颗粒在土颗粒的孔隙间不断运动,并在坡体内部汇集,使得坡体含水率增大,当坡体内部含水率接近饱和时,土颗粒间的黏结力被破坏,坡体抗剪强度丧失,发生流滑。宏观上表现为后部土体下沉,推动前部土体向下快速运动。通过数值模拟和离心模型试验试验 现象的对比,可以看出数值模拟基本上再现了离心模型试验的试验过程,且坡体内部水分的分布情况也与离心模型试验基本一致,说明本文的数值模拟方法具有可行性。
图6为采用小颗粒方法对离心模型试验进行模拟的数值模拟和离心模型试验现象对比图。
将图5和图6对比可以看出:两种方法都较好的模拟了离心模型试验中坡体发生整体流滑的现象,坡体内部水分的分布情况也与离心模型试验基本一致。稍有不同的是,采用小颗粒方法进行模拟时,在试验初期更接近离心模型试验现象,坡脚处含水率低,坡体后部出现了明显的下沉。而在试验后期,由于颗粒数量多,水颗粒运动速度较快,坡体后部土体流动更快,破坏规模要比采用大颗粒方法时更大,水颗粒的汇集会将部分土颗粒挤到坡体上方。
图7和图8分别为坡体在降雨作用下形成滑坡过程中土颗粒位移矢量和速度矢量的变化情况。

图5 大颗粒方法数值模拟与离心模型试验现象对比图Fig.5 Comparison of numerical simulation and centrifuge test

图6 小颗粒方法数值模拟与离心模型试验现象对比图Fig.6 Comparison of numerical simulation and centrifuge test
对土颗粒的细观运动进行分析,在试验初期,坡体后部土颗粒的运动方向以竖直向下为主。此后,土颗粒速度随时间的增加呈增大趋势,其中以土体后部的颗粒速度最大,坡体后部速度较大的原因是水颗粒的快速流动破坏土颗粒间的黏结力,后部土体坍塌呈散粒体状态,这将造成后部土体颗粒高度方向上的更大分离和相对运动。而中部土颗粒的运动方向以平行于坡面方向为主,且位移矢量要大于坡体前部,使得坡体有向下运动的趋势,土体内部土颗粒受到斜槽底部摩擦作用和坡脚土体的束缚作用较大,使得土体颗粒的速度分布相对均匀。前部土颗粒的运动则以平行于坡底方向的向下运动为主,距表层越近的颗粒位移越大,这将造成土体颗粒的剪切和错动,但运动速度较小。坡体前部速度较小的原因可能是前部水颗粒较少,土体呈非饱和状态,颗粒间的黏结力相对较大。上述颗粒速度、位移大小和方向的差异,使得原本规则的坡体向波浪状发展,当滑坡形成时,坡体是以一个整体快速向下滑动的。

图7 土颗粒位移矢量变化图Fig.7 Variation of displacement vector of soil particles

图8 土颗粒速度矢量变化图Fig.8 Variation of velocity vector of soil particles
为了验证数值模拟结果的可靠性,在离心模型试验中设置数码显微镜对土坡局部土体进行细观观测,观测位置及细观运动结果如图9所示。

图9 细观观测区域在坡体位置Fig.9 Mesoscopic analysis area of debris flow slope
1#、2#观测点的细观观测图片如图10所示。由图10可知,试验初期,雨水的入渗导致坡体沉降,由于坡脚上方没有降雨,此时坡脚处颗粒几乎没有变化,而坡体中部颗粒发生明显的下沉,可以看到颗粒 A 主要发生竖向移动,粗颗粒骨架之间的孔隙减小。随着降雨的进行,坡脚处细观观测区域内沿斜坡方向出现大量细颗粒,填充了粗颗粒骨架间的孔隙,坡脚处的颗粒A发生沿斜坡方向的移动。坡体中部细颗粒同样有所增加,且土体的含水率明显升高。观测区域内颗粒A的竖向位移增大,同时也发生了一定的水平位移。降雨进行到 420 s时,标志颗粒A已运动出观测区域,坡脚处含水率增加,但土体饱和度较低,结合宏观现象可知坡脚处没有雨水渗出。而在坡体中部,观测区域内细颗粒含量明显增多,且含水率很高,土体接近饱和状态,坡体中流动的孔隙水带动细颗粒向下迁移。数值模拟得到的颗粒细观运动规律与离心模型试验观测到的宏观现象及细观试验结果基本一致。
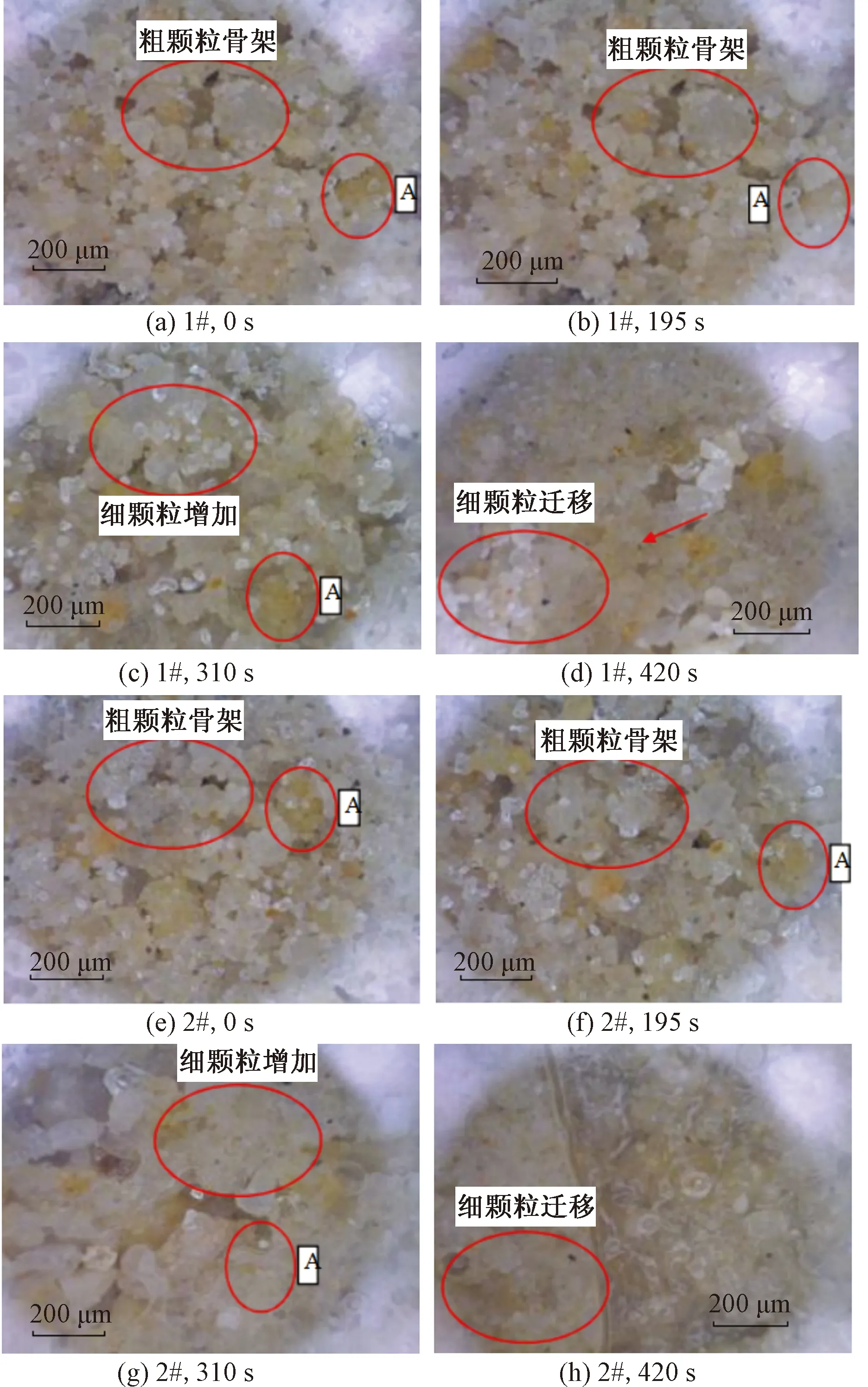
图10 细观观测图片Fig.10 Mesoscopic observation images of analysis area

图11 水颗粒速度矢量变化图Fig.11 Variation of velocity vector of water particles
图11为数值模拟时,水颗粒的速度矢量变化图。从图11中可以看出,在试验初期,水颗粒的速度矢量方向近乎垂直于土体表面,最大的流速出现在坡体表面处。坡体内部水颗粒分散分布,颗粒速度较小。随着降雨的进行,坡体内部水颗粒的速度开始增加,且坡体后部水颗粒的速度大于坡体前部,最大渗流速度在坡体中部位置,在水颗粒的作用下,坡体呈整体流滑破坏。
水颗粒在坡体内部聚集并逐渐向坡体下方运动,可以看出坡体下部水颗粒的速度明显大于上部。降雨入渗使得水进入到坡体底部,并在底部集聚使得流速逐渐增大,在水颗粒的携带下,发生整体流滑的松散土颗粒与水颗粒混合在一起,向下运动。水颗粒速度的变化从细观方面反映了滑坡的形成过程。
图12为滑坡形成过程中土颗粒间的接触力分布情况。
土颗粒间的接触力主要是由重力引起的,在滑坡发生前,接触力沿坡体高度方向递增分布,坡体下部接触力较大。此时土体前部颗粒间的接触力相对比较小。粗砂坡体是个具有散体颗粒性质的集合体,由于试验中存在一定的初始含水率,使得颗粒之间存在一定的黏结力,坡体成一个整体。在降雨的作用下,水颗粒的运动导致土体发生整体流滑破坏,表现出散体性质,土体间的接触力基本分布在土体的前部,而此时滑坡体后部的接触力很小。土体颗粒接触力的变化表明,粗砂坡体在降雨作用下逐渐转变,这种转变的过程将使得土颗粒的受力和颗粒的接触性质发生变化。这从细观层面证实了离心模型试验中得到的滑坡形成过程中,坡体内部含水率的变化情况,即认为滑坡体的头部土体含水率较低,固体颗粒性质起主要作用,固体颗粒的接触产生了接触力,而滑坡体的后部基本呈流态状,水体的浮力和润滑作用,导致颗粒间的接触力下降。
图13给出了水颗粒在下滑过程中颗粒间的接触力分布情况。水颗粒间的接触力变化可以近似体现坡体内部含水率和孔隙水压力的变化情况。在试验初期,坡体内部的水颗粒分散分布,因此水颗粒间的接触力较小,可以认为此时坡体内部处于非饱和状态,土颗粒间有较大的基质吸力。基质吸力的存在使得坡体处于初始稳定状态。随着雨水的不断下渗,水颗粒开始相互连接,并在坡体内部汇集,水颗粒间的接触力明显增大,宏观上表现为坡体内部含水率和孔隙水压力的升高。孔压的升高使得土颗粒间的基质吸力丧失,土体抗剪强度降低,当抗剪强度减小到一定程度后,在重力的作用下,坡体发生整体流滑,并迅速流动。

图12 土颗粒接触力分布图Fig.12 Distribution of soil particle contact force

图13 水颗粒接触力分布图Fig.13 Contact force distribution of water particles
综合土颗粒和水颗粒的接触力变化情况可知,由降雨诱发的砂土坡体在滑动过程中,会导致坡体内部受力和颗粒性质发生根本变化。
结合上述数值模拟结果,从细观的角度来分析滑坡的形成机理,在滑坡形成前,土颗粒之间相互接触,土颗粒间的接触力和黏结力使得坡体处于平衡状态,具有一定的强度。随着试验的进行,水颗粒在坡体内部运动,对土颗粒施加作用力。当水颗粒的作用力大于土颗粒之间的黏结力时,土颗粒之间开始发生错动,重新调整位置,土颗粒之间的孔隙减小。如果此时孔隙间的水颗粒无法渗出,土颗粒会悬浮在水颗粒之中,土颗粒间的接触减少甚至脱离,土颗粒之间的相互作用力将转化为土颗粒与水颗粒之间的作用力,土体出现流体特征,抗剪强度丧失,此时说明坡体已经发生流滑,随后土颗粒与水颗粒混合在一起向下快速运动。
4 结论
(1)通过数值模拟现象和离心模型试验现象的对比,可以看出数值模拟基本上再现了离心模型试验的试验过程,且坡体内部水分的分布情况也与离心模型试验基本一致,说明本文改良后的数值模拟方法具有可行性。
(2)从数值模拟结果来看滑坡的形成机理为:孔隙间的水颗粒无法渗出,土颗粒会悬浮在水颗粒之中,土颗粒间的接触减少甚至脱离,土体出现流体特征,抗剪强度丧失。
(3)从细观的方面来看,滑坡有两种可能的发展过程:一是如果整个坡体完全滑动,坡体内部各处水颗粒施加给土颗粒的作用力与此位置土颗粒的接触力正好相等(此时土颗粒不再传递接触力),坡体流滑;另一种是前部土体没有完全破坏,水颗粒施加给土颗粒的作用力要大于第一种情况,或者说等于土颗粒重力和前部土颗粒的接触力之和时,坡体发生流滑。从这个细观机制来说,流滑应该首先从后部产生,然后向前部发展。

