无系统误差的CPⅢ精密三角高程控制网仿真研究

李建章

(1.兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070; 2.地理国情监测技术应用国家地方联合工程研究中心，甘肃 兰州 730070; 3.甘肃省地理国情监测工程实验室，甘肃 兰州 730070)

CPⅢ控制网点数多，点位密集，利用精密水准建立高程控制网外业工作量大，效率低下，因此研究利用CPⅢ平面控制测量中的竖直角、斜距观测值构建精密三角高程控制网成为一个热点方向。

精密三角高程测量受到竖直角观测误差和斜距观测误差的影响，也受到大气折光、地球曲率、垂线偏差等系统性误差的影响[1]。系统误差由于具有累积性，对于CPⅢ精密三角高程控制网最终解算精度有较大的影响，因此如何消除系统误差的影响，是建立合格CPⅢ精密三角高程控制网的关键。

文献[2]通过构建差分观测值削弱球气差的影响，文献[3]则通过参数法来消除球气差的影响，都取得了良好的效果。但这些研究成果在现有条件下也不能保证所有的点都附合规范要求，如参数法要求高程基准点间距达到0.5～1 km才能获得附合规范要求的CPⅢ高程控制点，但实际线路水准点基点间距为2 km。在未来的研究中需要进一步提高CPⅢ精密三角高程控制网的精度，是降低偶然误差的影响还是进一步削弱残余系统误差的影响，这是首先需要解决的问题。

本文通过仿真数据研究在无系统误差影响下CPⅢ精密三角高程控制网可达到的精度，以及起算点密度、观测测回数等对CPⅢ精密三角高程控制网的影响规律，为CPⅢ精密三角高程控制网的下一步研究提供有力的支撑。

1 无系统误差影响的CPⅢ精密三角高程控制网平差模型

由于不考虑系统误差影响，因此选择非差模式构建CPⅢ高程控制网。如图1为CPⅢ平面控制网i测站观测示意图，其中实心正方形、实心圆圈、空心圆圈分别为线路基准点、测站点和CPⅢ点。

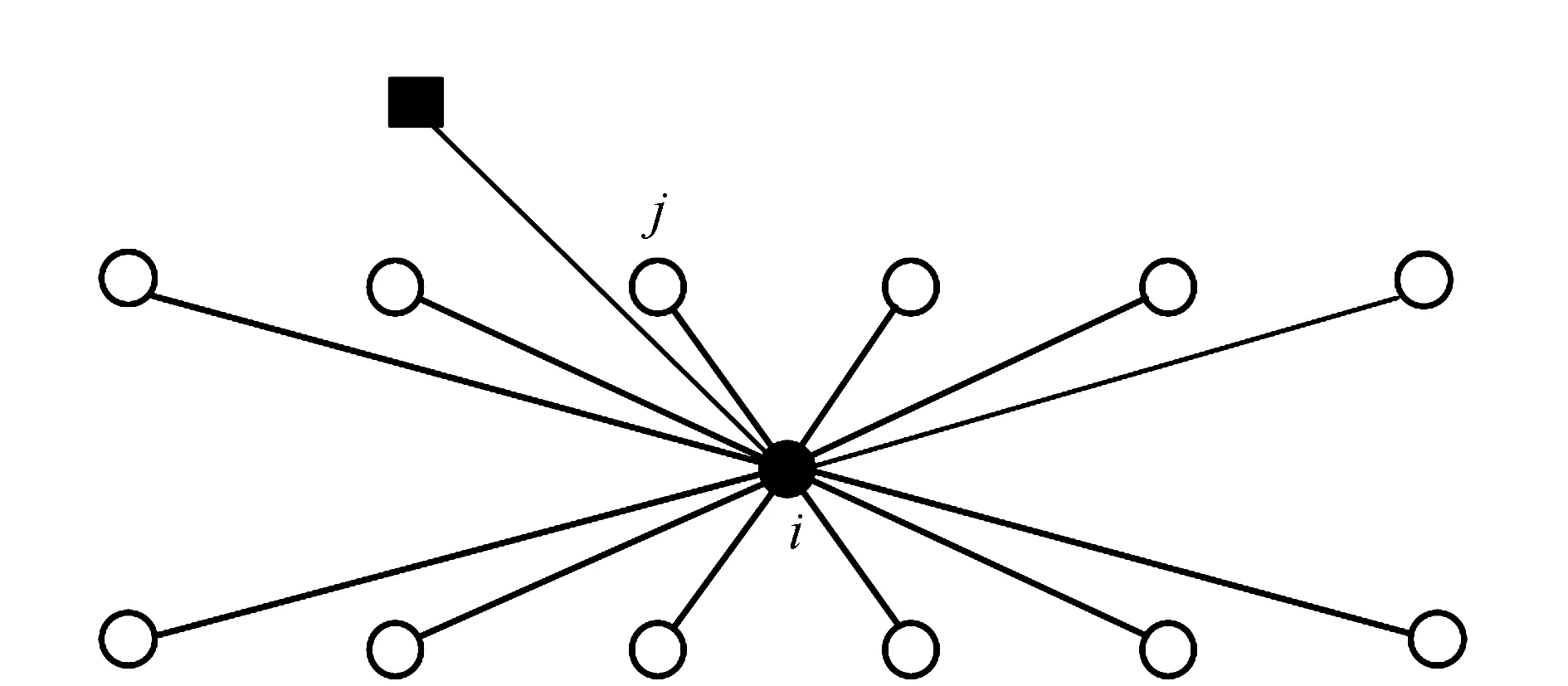
图1 CPⅢ精密三角高程控制网i测站观测示意图

在测站点i对各目标点进行观测，可获得竖直角、斜距以及方向观测值，其中竖直角和斜距观测值可进一步形成三角高程观测值。设对j点观测所得竖直角和斜距观测值分别为βij、Sij，则可得三角高程观测值：

hij=Sij×sin(βij) .

(1)

又设i、j两点最或然高程值分别为yi、xj，则：

hij+vij=xj-yi.

(2)

则得该观测值误差方程为：

vij=xj-yi-hij.

(3)

如果j点为已知点，且其高程为Hj，则其误差方程为:

vij=xj-yi-(hij-Hj) .

(4)

设有n个观测值，m个测站，t个CPⅢ高程点，则可写出如下矩阵形式的误差方程:

V=BX-l.

(5)

其中

(6)

依最小二乘法，可得待求参数最优估值

X=(BTPB)-1BTPl.

(7)

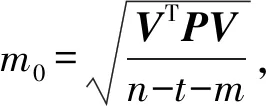
(8)

2 CPⅢ精密三角高程控制网仿真

由式(6)可知，B矩阵各单元值仅为1或-1两种结果，与CPⅢ点的高程、平面位置无关，仅反映了各点间的连接关系。由式(7)可知，待求参数估计值X与起算数据、原始观测值、观测值间的权比关系以及B矩阵有关。而由式(5)可知，观测值改正数与B矩阵、权阵以及X矩阵有关。

综上可知，待求参数的方差值与CPⅢ点的具体的高程、平面位置无关，只与各点间的连接关系、起算数据、原始观测值以及观测值权矩阵有关。因此CPⅢ精密三角高程控制网的仿真从两方面进行。

2.1 点位的仿真

如图2所示，首先建立一平面直角坐标系统。点位仿真具体步骤如下：

图2 CPⅢ仿真控制点示意图

1)确定起始点坐标及高程，如(x0,y0,H0)，且纵横坐标及高程各加一随机数。

2)设CPⅢ点个数为n，则各点的坐标及高程如下：

式中，i为CPⅢ点序号；Δxi、Δyi、ΔHi为随机数[5]。

3)选定线路基准点。为简化程序设计思路，基准点与其最近的CPⅢ点绑定到一起。

式中L为基准点与左侧CPⅢ点的横向间距。

4)对所得各点坐标矩阵左乘一旋转矩阵，即：

式中θ为(0-360)之间的一个随机数。

2.2 原始观测值及误差的仿真

CPⅢ平面控制网测量时，要保证每个目标点(包括基准点)至少要在3个测站各观测一次。第一测站及最后一测站各观测4个CPⅢ点，第二测站及倒数第二测站各观测8个CPⅢ点，其余各测站每次观测12个CPⅢ点。当CPⅢ点附近有基准点时，要对基准点进行联测。由于基准点和CPⅢ点有绑定关系，因此每次搜索到被绑定CPⅢ点，就可以搜索到绑定的基准点。

搜索当前测站需要观测的目标点，再计算测站坐标及高程。

式中，u为当前测站的观测点个数；Δnc、Δec、ΔHc为随机数。

则各方向观测值为：

式中，αi、βi、si分别为目标点相对于测站点的方向观测值、竖直角观测值以及斜距观测值。θ为定向角，介于(0-360)之间的一个随机数。Δα、Δβ、Δs为方向观测误差、竖直角观测误差以及斜距观测误差，是正态分布的随机数，在MATAB软件中通过函数normrnd来产生[6]。

每测站生成一独立的观测值文件，按照RLT格式存储。

3 仿真试验研究

依据文献[7-8]，要求CPⅢ高程中误差小于1 mm，相邻两点间高差中误差小于0.5 mm。现以TS30测量机器人为仿真对象进行试验，该仪器测角标称精度为0.5 s，测距标称精度为0.6+1 ppm。试验主要验证以下几个问题：

1)在工程现场目前条件下，无系统误差影响下的CPⅢ精密三角高程控制网所能达到的精度。

2)增加线路基准点密度，CPⅢ精密三角高程控制网精度的变化。

3)增加测回数，CPⅢ精密三角高程控制网精度的变化。

4)测距误差对CPⅢ精密三角高程控制网精度的影响。

由于在实际工程中，CPⅢ点绝对高程中误差较相邻点间的高差中误差更容易满足规范要求，因此本文只列出相邻点间的高差中误差曲线。

方案一：线路基准平均点间距为2 km，试验线路长分别为4 km、8 km、12 km，每测站观测3个测回。

从图3—图5可以看出，在线路基准点间距为2 km的条件下，线路长度增加，CPⅢ精密三角高程控制网精度变化可以忽略不计。

图3 4 km线路相邻点间高差相对中误差曲线

图4 8 km线路相邻点间高差相对中误差曲线

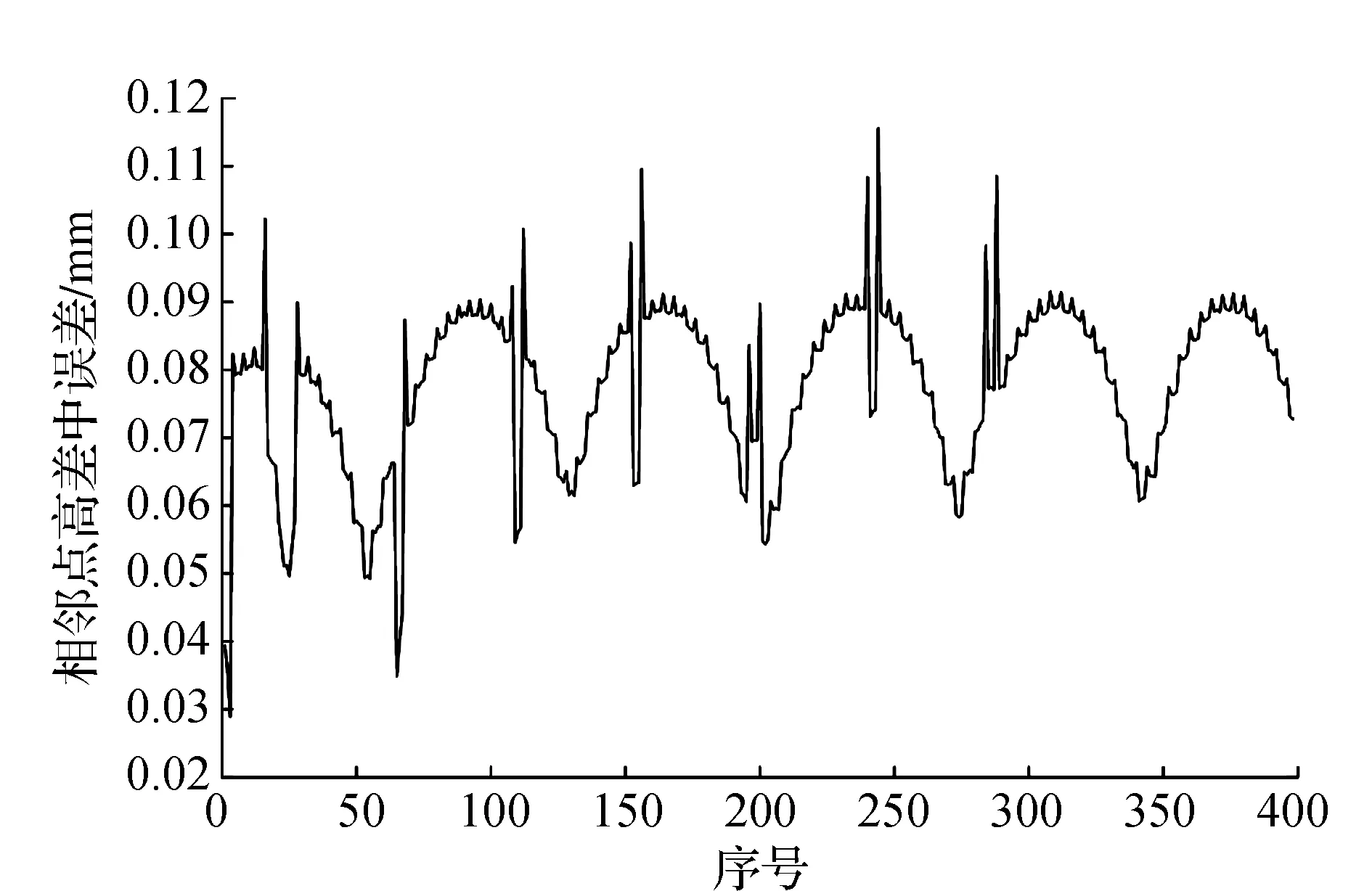
图5 12 km线路相邻点间高差中误差曲线

方案二：以线路长为12 km的CPⅢ精密三角高程控制网为例进行试验，基准点间距取1.7 km、1 km、0.48 km、0.24 km。

由图6可看出，控制网整体精度随着基准点密度的增大而逐渐提高，但提高幅度不大，且提高幅度逐渐变小。

方案三：线路基准平均点间距为2 km，试验线路长12 km，试验在二测回、三测回、四测回、五测回条件下的邻点间高差中误差曲线。

由图7可知，随着测回数的增加，控制网整体精度也有所提高，但提高幅度逐渐减缓。

方案四：线路长4 km，线路基准点间隔为2 km，CPⅢ点间高差可最大达10 m。要求观测3测回，测角误差为0，仿真数据解算结果如图8所示。

由图8可知，在CPⅢ精密三角高程测量中，距离测量误差对控制网最终解算精度的影响可以忽略不计。

图7 12km线路不同测回数条件下相邻点间高差中误差曲线

图8 12 km线路无竖直角观测误差下相邻点间高差中误差曲线

4 结束语

本文通过仿真数据研究了无系统误差影响下线路长度、测回数、基准点间距等因素对CPⅢ精密三角高程控制网精度的影响。通过试验可知：

1)在没有系统误差影响的情况下，相邻CPⅢ点间高差中误差小于0.15 mm，完全可以达到精密水准测量的精度[11]。然而通过大量实测数据解算发现大多CPⅢ精密三角高程控制网的解算精度在0.4 mm左右，这说明实测控制网中系统性误差残余误差依然是存在的。

2)通过增加测回数、增加线路基准点密度来降低偶然误差的影响，这对控制网最终解算精度的影响是非常有限的。

3)测距误差对控制网解算精度的影响可以忽略不计。

系统误差具有累积性，往往会导致控制网整体精度的下降，致使部分成果超限。文献[4]通过参数法消除CPⅢ精密三角高程控制网中球气差的影响，取得了良好的效果。因此在下一步的研究中，垂线偏差对CPⅢ精密三角高程控制网的影响及其规律是要研究的重点内容。