数学教学中“圆的周长”教学思考

陈励群

摘 要：在“圆的周长”一课的教学中，教师应从数学自身内在发展的需要出发，引导学生猜想圆的周长与直径的关系，并用不同的方法测量圆的周长，从而计算、验证得出圆周率，使学生的知识掌握得更加扎实。

关键词：数学教学;圆的周长;新课;有效猜想;测量

中图分类号：G623.5 文献标志码：A 文章编号：1008-3561（2019）24-0059-01

数学扎根于现实生活，还扎根于数学自身发展的需要。在苏教版教材第十册“圆的周长”的教学中，教师可从数学自身发展的需要入手，直接引导学生猜想圆的周长与直径的关系，再通过演示、推理得出“圆的周长应该是直径的3倍多一些”，最后通过动手操作用不同的方法量出圆的周长和直径的长度，通过计算、验证得出圆周率。

一、新课引入

很多教师的新课引入都是从生活情境着手的。例如，小红一家三人骑规格不同的自行车去秋游（出示图1），三个车轮滚动一周，哪一个滚得远一些？这就是我们今天要研究的问题。（揭题：圆的周长）其实这个问题学生已经从日常生活中知道了答案：车轮的直径越大，滚动一周的路程也就越长，这样的引入在教师看来虽然比较形象，但对圆的周长学习不一定有多大的帮助。数学扎根于现实生活，还扎根于数学自身发展的需要，教师应从数学自身发展的需要去引入。

从学生已有知识基础“长方形和正方形的周长”的话题引入，也是一种有效的引入方法。师：我们已经认识了圆，根据以前学习长方形和正方形的经验，你们猜一猜今天我们将会学习什么？学生很容易想到将要学习圆的周长。师：大家想一想圆的周长是指圆哪儿的长度？圆的周长可以像长方形、正方形那样用一个公式来计算吗？有的学生觉得可以，有的学生觉得不可以，因为在学习三角形和梯形时，教材就没有给出这两种平面图形的周长计算公式，而且圆是一个曲线图形，可能没有计算周长的公式。教师出示课本例题的主题图——3种不同规格的车轮图，让学生在课本上描出这三个车轮的周长，再引导学生猜想：圆的周长可能与圆的什么有关？学生很容易猜想出圆的周长与圆的直径有关，并得出直径越长周长就越长的感性认知。教师加以肯定：同学们的观察能力真强，圆的周长确实与圆的直径有关系，而且只要用圆的直径乘一个固定的数就得到这个圆的周长，今天我们就来找出这个固定的数是多少，以及圆的周长和直径的关系。

二、引导学生进行有效猜想

引导学生先猜想，再通过动手操作、计算、验证圆周率，是教师经常采用的教学模式和策略，这说明教师已经深知“猜想——验证”在学生探究、发现学习中的作用。但只有少数教师让学生进行两个层次的猜想：（1）先引导学生猜想圆的周长与直径的长度有关，直径越长，周长也越长;（2）在此基础上再猜测出：圆的周长应该在直径的3倍与4倍之间。这说明教师对猜想这一环节的认识还停留在比较浅的层面，没有引导学生进行探究學习所需要的猜想，猜想没有为探究学习提供必要的帮助，如果确定了圆周率的取值范围，这个范围就能如大海中的灯塔一样指引着学生探究学习的正确方向，使学生探究学习的目的性更强，让学生更容易找到正确答案。

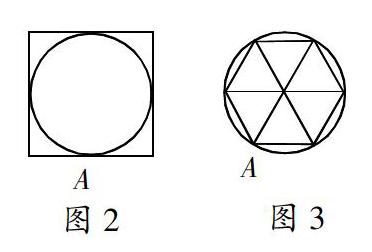
教师可先出示图2，引导学生思考：如果有两只小蚂蚁从“A”点出发，进行赛跑，一个沿正方形的边跑，一个沿圆的一周跑，这样的比赛公平吗？学生得出圆的直径和外面的正方形的边长相等，所以圆的周长应该比直径的4倍少一些。教师再出示图3，还用两只蚂蚁从“A”点出发进行赛跑的情境为例，一个沿正六边形的边跑，一个沿圆的一周跑，这样的比赛公平吗？让学生通过比较、思考得出：圆内接正六边形的周长正好是直径的3倍，而圆的周长应该比直径的3倍多一些。这两次不公平的比赛，形象、生动地让学生依靠推理、猜想得出圆的周长和直径之间的关系：圆的周长应该是直径的3倍多一些，而不足直径的4倍。那么究竟是直径的3倍多多少呢？在此猜想的基础上，学生很容易想到：在现有知识和现有的工具基础上，可以通过测量来算出圆的周长与直径之间的关系。

三、测量圆周长的方法

在引导学生量圆的周长时，许多学生想到的方法就是用课本提供的——“绕圆法”和“滚圆法”测量出圆的周长，并算出所测周长与直径之间的关系，但是用这两种方法测量圆的周长是很不容易操作的。

类似圆的周长这一类探究性比较强的课型，教师可以不让学生进行预习，直接让学生原生态地进行探究发现，体验头脑风暴的过程。教师都有这样的经历：在以往学生预习的课堂中，往往会出现学生用直尺量出周长是6.28厘米和9.42厘米这些迎合教师的“人造数值”。在如何测量圆的周长时，教师可进行这样的引导：圆的一周是弯曲的，而我们平时测量的工具却是直尺。学生通过小组交流讨论得出：只有化曲为直才行。学生可以用软尺直接去量圆的周长，也可以用课本中的滚圆的方法，说不定就有学生想到将一个圆形纸片对折几次后，量出一份的长度再乘份数。

参考文献：

[1]韩礼秀.两次执教“角的度量”后的思考[J].小学教学，2010（04）.

[2]周丹丹，蔡宏圣.“圆的周长”教学实录与评析[J].小学数学教育，2018（05）.