基于GAN网络的机器人逆运动学求解
尹一伊,朱其新,张国平,朱永红
(1.苏州科技大学 电子与信息工程学院,江苏 苏州215009;2.苏州科技大学 机械工程学院,江苏 苏州 215009;3.深圳市大族机器人有限公司,广东 深圳 518058;4.景德镇陶瓷大学 机电工程学院,江西 景德镇 333001)
机器人逆运动学求解是根据给定的机器人末端执行器位置和姿态求解机器人各关节的关节变量,它是机器人离线编程和轨迹规划的前提,是机器人运动控制的基础[1]。
用于机械手逆运动学求解的方法较多,主要有代数法[2]、几何法[3]和数值解法[4]。代数法不能保证具有封闭形式解;几何法要求机械手的前三个节点的封闭形式解在几何上存在。此外,一类机械手的封闭形式解不能用于其他不同几何形状的机械手。数值解法依赖于起始点,可收敛于单一解。神经网络解法属于数值解法,因为具有并行处理、分布式存储和容错性的结构特征,而被广泛应用[5]。
考虑到常用于求解机器人逆运动学的神经网络方法(如RBF、BP)[6]以下不足:(1)深层网络使得收敛速度减慢,求解效率不高,求解结果有发散的情况存在;(2)无法解释推理过程和推理依据;(3)神经网络极易陷入局部最优,导致模型泛化能力很差,使得模型过拟合得到的数据分布,并不能很好的预测未知的数据。
生成式对抗网络(GAN)是深度学习发展的成果,通过生成网络与真实数据的相互博弈得到尽可能真实的样本数据,由Goodfellow 等人[7]在2014 年提出。GAN 网络作为一种生成模型,被广泛应用于对真实数据的分布进行建模和生成真实数据。凭借这一能力,它被认为解决了传统机器学习中数据不足的问题,对提高图像分辨率、图像仿真、自然语言的处理都能达到理想的效果。除此之外,GAN 还涉及许多其他内容,包括机器人、加密与安全、天体物理等,是深度学习研究中重要领域。GAN 网络的生成数据复杂度是线性相关,先验假设非常少,这意味着它可以生成比其他模型更精确的样本[8]。
基于目前研究中少有人关注GAN 网络在机器人逆运动学中的应用,笔者提出使用GAN 神经网络来建立机器人逆运动学模型,利用GAN 泛化能力强、训练效率高等优点,将GAN 生成的高精确度样本视为最终逆运动学的结果,最后可以得到比其他神经网络处理机器人逆运动学更有效率的计算过程和精确的结果。
1 机器人运动学问题
D-H(Devanit-Harenberg)分析法通常用来描述机器人相邻连杆之间的运动学关系。D-H 描述法中典型的串联机器人由关节和连杆组成[9-11],每个关节包括一个自由度,或者是平动关节,或者是转动关节。对拥有n 个关节的机器人,就有从 0 到 n 的(n+1)个连杆。连杆 0 是机器人基座,通常是固定的,连杆n 携带工具端。
为此,给每个连杆固定一个参考坐标系,确定从一个关节到另一个关节的变换步骤,最后得到末端执行器坐标系相对于基坐标系的等价齐次变换矩阵。
机器人相邻连杆之间的相对关系可用四个参数表示,分别为描述两相邻关节轴线间相对位置关系的连杆长度ai和连杆扭角αi,以及描述相邻两连杆之间位置关系的连杆距离di和连杆夹角(关节角)θi,连杆参数示意图如图1 所示。
从i-1 坐标系到i 坐标系,只需完成下述变换:
(1)沿 Z(i-1)轴平移距离 di,使得 X(i-1)轴与 Xi轴相交;
(2)绕 Z(i-1)轴旋转角度 θi,使得 X(i-1)轴与 Xi轴重合;
(3)沿Xi轴平移距离ai,使得i-1 坐标系的原点与i 坐标系的原点重合;
(4)最后绕 Xi轴旋转角度αi,使得两坐标系完全重合。
根据链式法则,相邻连杆之间的位姿转换关系可用下式表示
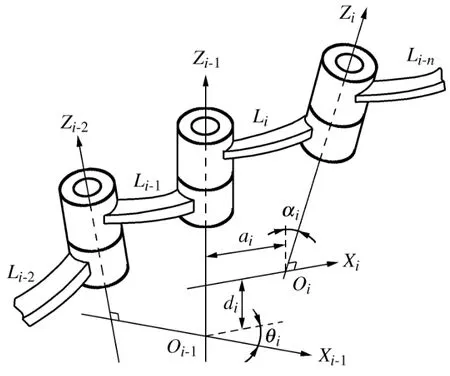
图1 相邻连杆参数示意图
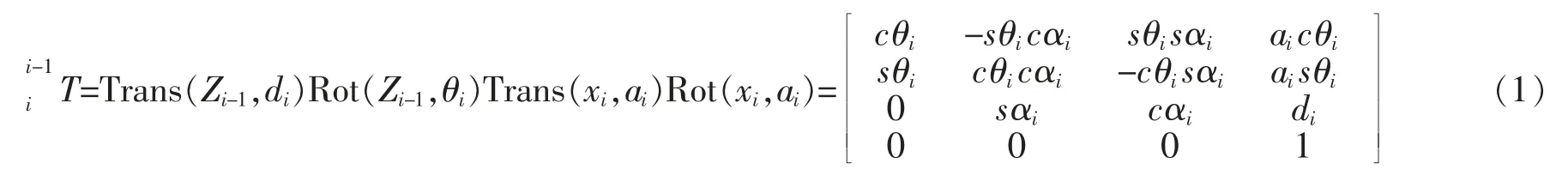
建模所用机器人是深圳大族集团生产的Elfin-5 六自由度机器人,其相关参数:工作范围为800 mm,关节范围为+/-178°,关节速度为90°/s,安装面积为Φ156 mm,自由度为6 个旋转关节,外部电源输入为100~240 V,50~60 Hz。
给该型号机器人建模得到D-H 参数表,见表1。

表1 D-H 参数
将建立坐标系后的机器人从基座到第一关节,再从第一关节到第二关节直到最后一个关节,就得到机器人总的变换矩阵(即机器人运动学方程)
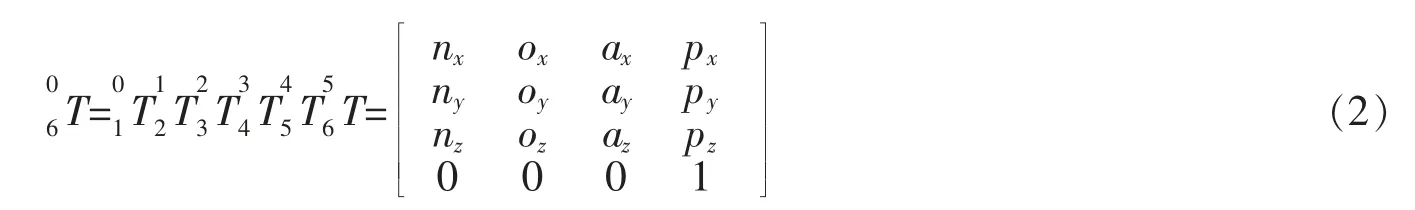
2 生成式对抗网络(GAN)
生成式对抗网络(GAN)是由Goodfellow 等人[7]在2014 年提出的一种生成式模型,其核心思想来源于博弈论中的二人零和博弈。由一种对抗性神经网络构成,分别称生成器和判别器,生成器试图生成可被判别器误认为真实样本的生成样本[7]。GAN 的网络结构如图2 所示。
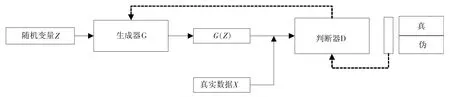
图2 GAN 原理图
GAN 优化和训练的过程是一个博弈问题,即极大化判别模型的判断能力,极小化生成模型输出被判断为伪造的概率[12-13]。
GAN 核心原理算法描述如下:
生成模型G 学习真实数据X 的概率分布,尽可能让判别模型认为是“真实”的。
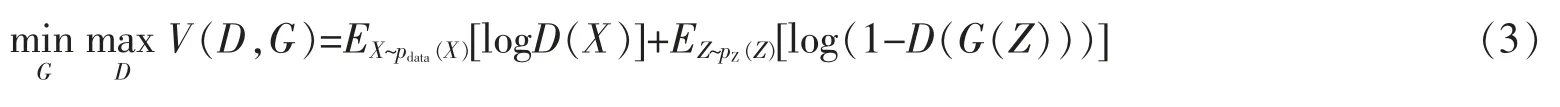
其中 Z 表示从特定分布 p(Z)中随机采样所得的向量,pdata(X)表示真实样本数据的概率分布;G(Z)表示生成网络由噪声Z 生成的样本,D(X)表示真实样本X 通过判别网络判断其为真实样本的概率,D(G(Z))表示生成样本通过判别网络后,判断其为真实样本的概率,它被期望越接近1 越好。
判别网络的目的是让 D(X)接近 1,D(G(Z))接近 0。GAN的训练过程是将D 的错误概率最大化的过程,同时生成器将log(1-D(G(Z)))的期望达到最小化,提升自身生成能力,最终两者通过对抗交替训练,形成参数优化[14-15]。
在机器人逆运动学训练中,用Matlab 生成随机输入变量,经过生成器G 生成伪造样本,与真实末端执行器位姿对应关节变量数据进入判别器进行判别。GAN 通过学习这些样本,得到样本数据分布,从而再次提供训练样本,辅助训练过程,达到监督学习的作用。需要说明的是,训练过程中,生成式对抗网络同时更新两个网络的梯度,使用随机梯度下降法求解。每次迭代对两个数据进行采样:真实样本X 和与真实样本同等数量的Z变量来生成样本,并同时更新两个模型的梯度,最终达到目标训练效果。
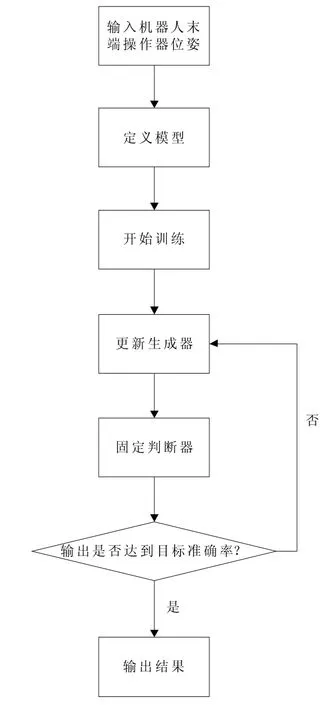
图3 GAN 算法求解机器人逆运动学流程图
3 系统仿真
为了验证GAN 网络在机械手逆运动学求解中应用的有效性,文中使用计算机仿真,平台选择Matlab。为了训练网络,学习样本文中选择大族Elfin-5 型工业机器人获取200 组真实数据,即机器人末端执行器位姿和对应关节变量。关节值表示为Q=[q1q2…qn]T,它与末端执行器位姿S 的关系通过机器人运动学反解 I(·)表示为 Q=I(S,φ),其中向量 φ 是造成机器人误差的所有几何参数,训练数据由代数法求出。使用训练后的GAN 网络对100 组末端执行器位姿值进行预测得到机器人逆运动学解即对应关节值后,将结果与实际值比较,得到结果。使用GAN 网络计算机器人逆运动学的算法流程如图3 所示。
按上述流程算法编写代码,运行结果如图4。

图4 GAN 网络训练值与实际值
接下来,为验证GAN 网络的训练效果,笔者使用广泛应用于机器人逆运动学中的BP 神经网络[16-18]对相同的200 组样本进行学习,在进行BP 网络分析时,隐层神经元数目设定为8。接下来,对BP 神经网络和GAN 神经网络预测数据进行一些处理。就GAN 和Matlab 中自带BP 网络而言,结果数值范围差别很大,如不处理,则数值大的数据将会反映预测结果,而数值小的数据反映不出预测结果,为避免这个问题,文中将得到的预测结果进行归一化误差处理。得到结果如图5、图6 所示。可以看到,Matlab 神经网络工具箱中BP 神经网络预测误差达到104级别,GAN 网络与预测误差在±0.8 范围内。
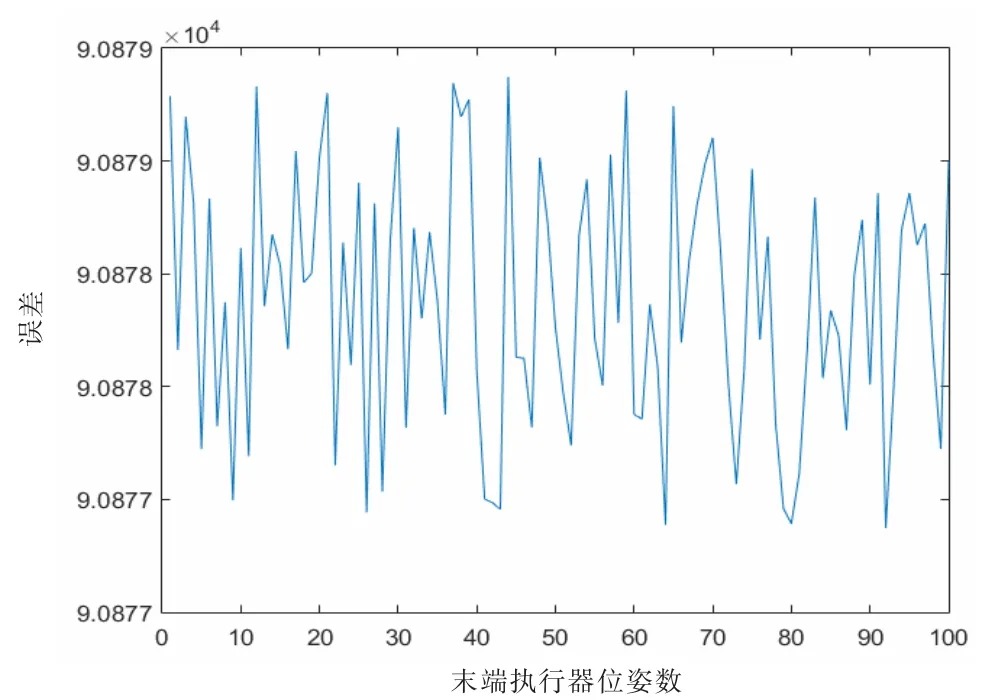
图5 BP 神经网络归一化误差

图6 GAN 神经网络归一化误差
4 结语
文中将GAN 神经网络引入机器人逆运动学运算中,并基于某实际型号的机器人建立了运算模型。随后将运算结果与BP 等神经网络运算结果进行了对比,得到结果。
研究分析表明,基于GAN 神经网络的机器人逆运动学求解方法是可行的。相比传统BP 等神经网络算法,GAN 网络具有泛化能力强、训练效率高的特点。程序运行过程显示,在相同训练次数下,GAN 网络消耗时间更短且收敛性较BP 神经网络更强。
文章创新点在于将GAN 神经网络应用于机器人逆运动学求解中,并证明其可行性。在适当增加训练次数情况下,是可以提高预测精度并在实际中应用的。接下来研究的重点将集中于提高计算精确度的具体解决方案。

