基于极点配置的PMSM位置伺服系统高阶对象的控制器设计
费清琪,朱其新,刘红俐,朱永红
(1.苏州科技大学 电子与信息工程学院,江苏 苏州215009;2.苏州科技大学 机械工程学院,江苏 苏州215009;3.景德镇陶瓷大学 机电工程学院,江西 景德镇 333001)
与传统的电励磁同步电机相比,永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有结构简单、运行可靠、体积小、质量轻、损耗小、效率高,以及电机的形状和尺寸可以灵活多样等显著优点[1]。近年来,随着永磁材料技术的不断发展,永磁电机控制技术的不断成熟,PMSM 在数控机床、航空航天、机器人等高性能伺服领域得到了广泛应用。
国内外学者对PMSM 进行了广泛的研究,文献[2]通过分析PMSM 的数学模型,设计了三闭环控制系统,并采用PID 控制器实现了系统的参数整定;文献[3]在PMSM 伺服系统三环控制的基础上,建立了电流闭环的控制模型,设计了电流环调节器并进行了控制参数的整定,提高了系统的控制性能;文献[4]针对PMSM 电流环的频域数学模型,设计了一种二自由度控制器,基于期望的系统阻尼比与上升时间,通过极点配置来得出控制器参数,仿真证明了其在兼顾电流环的跟踪性能及抗干扰性能的方面优于传统的PI 控制;文献[5]针对柔性负载系统,提出了三种基于极点配置的PI 调节器参数确定方法并分析了其各自的优劣势。
近几年随着智能控制领域方法的不断成熟,学者们通常会将模糊控制、神经网络、遗传算法等现代控制策略与传统控制方法相结合进行研究。文献[6]基于神经网络控制具有非线性、不确定性的特点,结合传统PID 控制、自适应控制等方法对永磁同步电机速度、位置控制问题及无传感器问题进行了研究;文献[7]为了满足伺服驱动控制器抗扰动能力及良好的速度控制能力,运用模糊控制规则结合极点配置算法来调整PI 调节器参数,设计出一种可以参数自调整的PMSM 伺服控制器并进行了仿真实验;文献[8]将状态反馈控制和模型辨识中的极点配置方法进行了改进,使之在被应用于非线性系统时也能具有较好的抗扰动能力。但是,上述文献并没有涉及到伺服系统高阶对象的控制器,一般情况下,可以通过永磁同步电机机械运动方程建立传统二阶模型,但传统的二阶模型无法很好地反映实际系统的相关物理特征,无法体现电流环参数变化对系统的影响。因此,通过数学分析的方法来建立精度更高的伺服系统的高阶模型是优化伺服系统控制的一个重点。文献[9]基于DSA 的PMSM 伺服系统速度环建模实验平台来建立了PMSM 速度环三阶、四阶和六阶的高阶数学模型;文献[10]根据被控量与PMSM 数学模型间的联系,基于拉氏变换构造了一种全系统的简化模型来对双闭环控制器的PI 参数进行整定;而文献[11-13]则针对高阶非线性伺服系统位置控制器的PID 参数优化问题进行了相关研究。而在对高阶对象的控制器参数进行极点配置设计时,极点参数的变化对控制器性能的影响,也是一个需要深入研究的课题。
笔者针对PMSM 伺服系统,首先基于PMSM 的系统数学模型,建立了PMSM 位置伺服系统的高阶传递函数模型;采用PID 控制策略,设计了基于极点配置的PMSM 位置伺服系统高阶对象控制器;针对高阶系统传递函数特征根具有不同解的情况,给出了PID 控制器的参数确定方法;仿真验证了极点配置方法的可行性,对极点参数变化时高阶系统不同的阶跃响应进行了对比分析,并给出了相关的参数选取范围。
1 永磁同步电机的数学模型
在解决实际问题的过程中,建立合理的数学模型对于分析系统的动态性能与稳态性能有着重要的作用。假设忽略铁芯的饱和,不计算涡流和磁滞损耗,电机中的感应电动势为正弦波,那么在d-q 坐标系中,PMSM的定子电压方程可以描述为

定子磁链方程为

那么由式(1)和式(2),可以得到

其中,ud和 uq分别为 d-q 轴的电压分量;id和 iq分别为 d-q 轴上的电流分量;Ld和 Lq为 d-q 轴上的等效电感;R 为定子电阻;ψd和ψq为d-q 轴上的定子磁链分量;ω 是电角速度;ψf是永久磁体对应的转子磁链。
在恒功率变换的原则下,得出电机的输出电磁转矩

其中p 为转子的磁极对数。
若忽略磁阻转矩,则令Ld=Lq,转矩方程变为

其中Kt为转矩常数。另外,电机的机械运动方程为

其中J 为转动惯量;ωm为机械角速度;TL为负载转矩;B 为阻尼系数。
2 位置环对象的建模
根据d-q 坐标系中的PMSM 数学模型可知,对PMSM 转矩的控制归根结底还是对d-q 轴的电流控制,而三环中最内一环的电流环则是提高响应速度、控制精度及性能的关键,为了实现PMSM 控制参数的解耦,使用较为常用的“id=0”控制策略,即令定子电流矢量与d 轴垂直,那么在永磁体的ψf是定值的情况下只需要通过调整iq,就可以实现对转矩的直接控制。文中基于“id=0”的控制策略建立伺服系统位置环对象的模型如图1 所示。
首先,PWM 逆变器的传递函数可以近似等效为一个一阶惯性环节,写成

其中KPWM为比例增益,TPWM为逆变器的时间常数。
由式(3),电机的传递函数为

其中 Ef为反电动势,Ef=ωmKe,Ke为反电动势常数,Ta为永磁同步伺服电机电气时间常数,Ta=Lq/R,Ka=1/R。
在忽略阻尼系数B 的情况下,由式(3)、(5)和(6),在电流输出加入负载环节后,其传递函数表示为

其中 Kt=Ke=pψf。
接下来就是电流调节器的设计,考虑到典型I 型系统的抗扰动恢复性能及跟随性能良好,故将电流环设计成典型I 型系统,采用PI 调节器,其传递函数为

其中Kp为PI 调节器的比例系数,τi为调节器的积分时间常数,τi=Kp/Ki,考虑到惯性环节对系统的延迟作用,为了提高电流环的响应速度,令调节器的时间常数τi等于电气时间常数Ta,则电流环加上PI 调节器后的开环传递函数为

其中

故此时电流环的闭环传递函数为
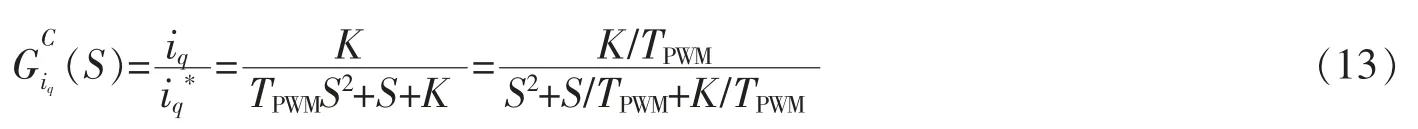
典型二阶系统,其闭环传递函数可以表示为

按照二阶模型的最佳整定方法,则

由式(13)、(14)可知

故由式(15)-(17)式可得

一般情况下TPWM较小,那么可以将式(13)近似为

其中Tq=1/K。
根据图1,得到PMSM 位置伺服系统电流环的高阶系统传递函数

3 控制器设计及参数整定
PID 控制器是一种线性控制器,它的传递函数可写成

式中 Kp、Ki、Kd分别是比例、积分、微分环节的参数。
整个高阶位置环路PID 控制器的系统框图如图2 所示。

图2 高阶电流环PID 控制器系统框图
设此闭环系统为单位反馈,由Gp(S)和G(S)已知,可以得到闭环系统的传递函数

得到系统的特征方程式

这时对于系统特征方程的根可以分解为两种形式,第一种形式
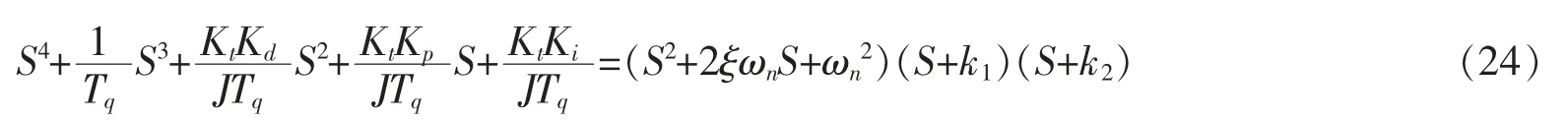
其中 ξ 为阻尼比,ωn为无阻尼振荡频率,k1和 k2为实轴极点与原点的距离。由此可知,只要确定 ξ、ωn、k1和 k2的值,那么根据式(24)系数相等的原则就可以计算出相应的Kp、Ki、Kd控制参数。
令式(24)中的 S2+2ξωnS+ωn2等于 0,得出其特征根

可以看出,当 0<ξ<1 时,S1,2为一对共轭复根;ξ=1 时,S1,2为一对重根;ξ>1 时,S1,2为一对不等负实根。因此,根据ξ 的取值不同,也可以将特征根分解为第二种形式
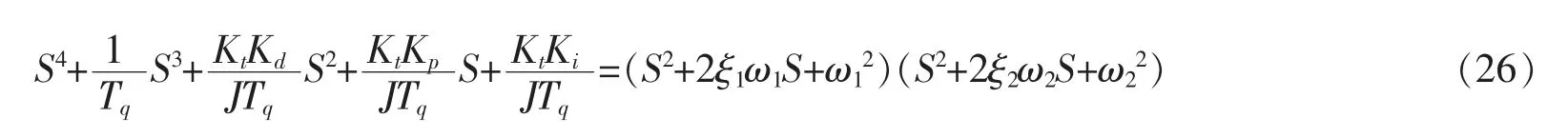
其中 ξ1、ξ2为阻尼比,ω1、ω2为无阻尼振荡频率。同理,只要确定 ξ1、ξ2、ω1和 ω2的值,也可以计算出相应的 PID控制参数。
下一部分的仿真实验将会着重分析ξ、ωn值的选取对系统极点分布及系统性能的影响。
4 仿真实验与分析
文献[5]基于其柔性负载系统的不同惯量比,两对极点的阻尼系数、实部与幅值是否相同的限制条件来进行极点配置PI 参数的整定。在文中,由于式(24)、(26)中存在多种变量,故采用控制变量的方法进行实验分析。
图3 为永磁同步电机位置伺服系统高阶模型的实际Simulink 仿真模型,其中电流环调节器的PI 参数可由式(12)求出,仿真模型的输入角度为1 rad。

图3 永磁同步电机位置伺服系统实际Simulink 仿真模型
仿真实验选取的仿真参数见表1。

表1 PMSM 仿真参数
4.1 第一种形式
第一种形式如式(24)所示,由于存在多个变量参数,故采取控制变量的原则进行仿真实验。
4.1.1 同阻尼比及实极点k1的极点配置策略
由式(25)可知,当 0<ξ<1 时,系统具有一对共轭复根及两个实数极点,故取 ξ=0.707,k1=15,ωn分别取10,20,30,40,50 rad·s-1时,控制器参数及系统仿真结果见表 2 及图4。

表2 同阻尼比及实极点k1 的极点配置参数
根据图4 所示仿真结果,在系统阻尼比及一个实轴极点不变的情况下,随着ωn的增大,系统调节时间变短,超调量增加,在 ωn大于 30 rad·s-1后系统开始出现振荡。

图4 同阻尼比及实极点k1 的极点配置仿真结果
4.1.2 相同无阻尼振荡频率及实极点k1的极点配置策略
取 ωn=30 rad·s-1,k1=15 时,ξ 分别取 0.4,0.707,0.9,1,2,4,仿真实验分为三种情况:当 0<ξ<1 时,系统具有一对共轭复根及两个实数极点;当ξ=1 时,系统在实轴上有一对负重根及两个实数极点-k1和-k2;当ξ>1时,系统具有两个不等负实根及两个实数极点-k1和-k2。将ξ=1 及ξ>1 的情况统一进行分析,控制器参数及系统仿真结果见表3 及图5、图6。

表3 相同无阻尼振荡频率及实极点k1 的极点配置参数

图5 相同无阻尼振荡频率及实极点k1 的极点配置仿真结果(0<ξ<1)
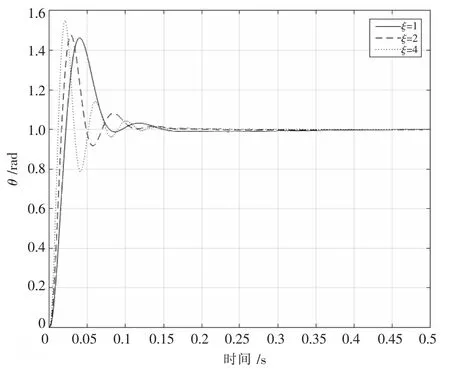
图6 相同无阻尼振荡频率及实极点k1的极点配置仿真结果(ξ≥1)
由图5 所示仿真结果可以发现,在无阻尼振荡频率不变的情况下,当0<ξ<1 时,随着阻尼比的增加,系统响应变快,调节时间变短,但慢慢出现小幅振荡。
由图6 所示仿真结果可以发现ξ≥1 时,随着阻尼比的增加,系统响应变快但振荡变大,且超调量增加,不利于实际工程的性能指标。
4.1.3 相同阻尼比及无阻尼振荡频率的极点配置策略
取 ξ=0.707,ωn=30 rad·s-1,k1分别取 1,5,10,15,30 时进行仿真实验,控制器参数及系统仿真结果见表 4及图7。
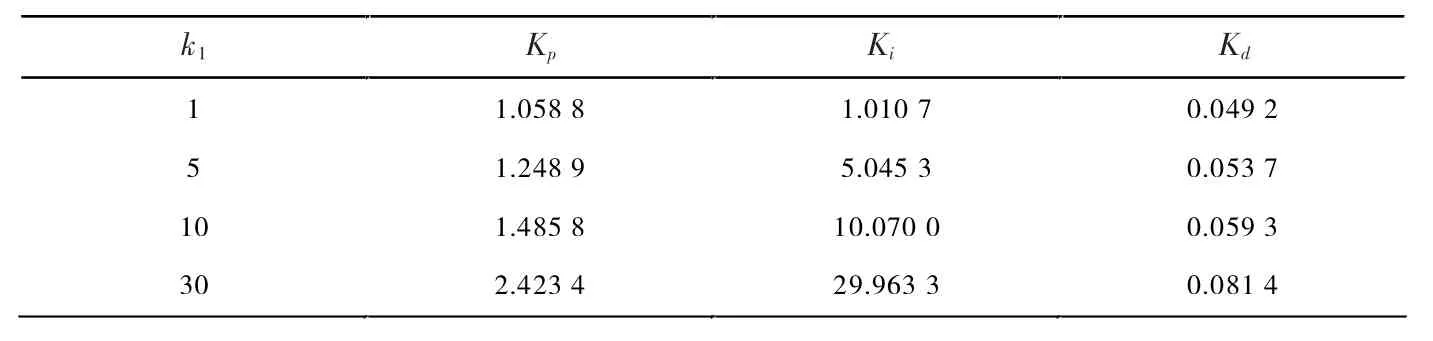
表4 相同阻尼比及无阻尼振荡频率的极点配置参数
由图7 所示仿真结果可以看出:随着k1的增大,系统响应变快,但超调量变大,系统开始出现振荡;而在k1较小时,系统超调量小,基本无振荡,稳定性好,但响应时间不是非常迅速。
由以上的分析,兼顾系统的快速性与稳定性,将参数取值范围大致总结为:阻尼比ξ 一般可以在0.6~0.8间取值;ωn可以在 20~40 rad·s-1间取值;k1可以在 10~20 间取值。
4.2 第二种形式
第二种形式如式(26),根据 ξ1、ξ2取值范围不同,分为三种情况讨论。
4.2.1 特征根为两对共轭极点的配置策略(0<ξ1、ξ2<1)
给定 ξ1=0.707,ωn=30 rad·s-1,分别取 ξ2=0.6,0.7,0.8,0.9 进行参数配置,控制器参数及系统仿真结果见表5 及图8。

表5 特征根为两对共轭极点的极点配置参数
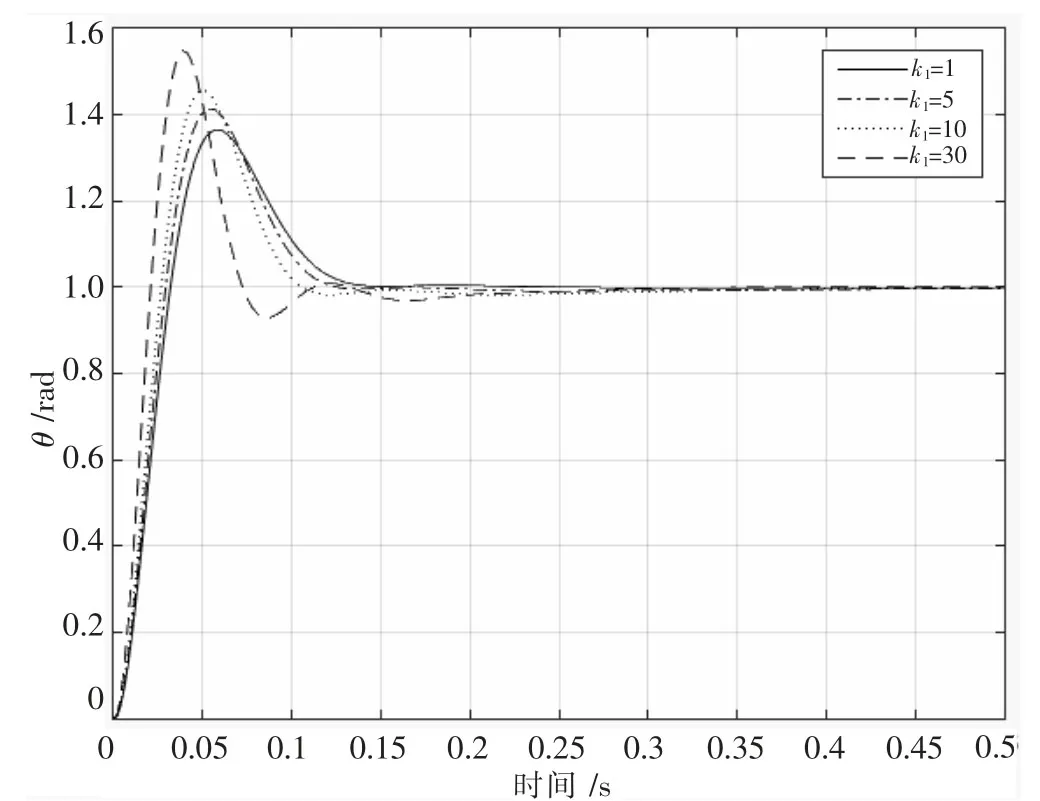
图7 相同无阻尼振荡频率及实极点k1 的极点配置仿真结果

图8 特征根为两对共轭极点的极点配置仿真结果
可以看出系统开始无响应,约0.45 s 后呈振荡发散状态,无法达到预期的目标响应。
4.2.2 特征根为一对共轭复数极点,一对实极点的情况(0<ξ1<1,ξ2>1)
取 ξ1=0.707,ωn=30 rad·s-1,ξ2=3,5,15,30 进行参数配置,控制器参数及系统仿真结果见表 6 及图 9。

表6 特征根为一对共轭极点、一对实极点的极点配置参数
根据图9 仿真结果所示,在ξ1和ωn不变的情况下,随着ξ2的增大,系统响应变慢,振荡及超调量变小,系统趋于稳定。
4.2.3 特征根为两对实数极点的情况(ξ1、ξ2值均大于1)
根据控制变量的原则,给定 ξ1=2,ωn=30 rad·s-1,分别取 ξ2=3,5,15,30 进行控制器参数配置,控制器参数及系统仿真结果见表7 及图10。

表7 特征根为两对实极点的极点配置参数

图9 特征根为一对共轭极点、一对实极点的极点配置仿真结果

图10 特征根为两对实极点的极点配置仿真结果
仿真结果可以看出:当一对实极点的位置不变,另一对的阻尼比增加时,系统超调量及振荡变小,系统趋于稳定,响应变慢。
5 结语
通过对永磁同步电机位置伺服系统高阶模型的建模与仿真,文中验证了此模型在搭配PID 控制器时具有较好的控制性能。仿真实验针对选取不同的ξ、ωn参数时系统的极点分布进行了研究;对极点参数变化对系统性能的影响进行了相关的实验,结合仿真实验给出了具体的ξ、ωn参数选取范围,具有一定的实际工程意义。相较于文献[5]中选定限制条件的参数配置的方法,文中基于极点分布进行参数配置的方法更为简单直观。在现代高精度伺服控制的要求下,位置环的超调量会对系统的性能指标产生较大的影响,因此,如何兼顾系统的快速响应能力与稳定性,对调节器模型进行优化,是该文进一步的研究方向。

