借助学科整合深入理解概率——《可能性》教学实践与思考（二）

陈芸芸

【教学内容】

人教版五年级上册第四单元。

【教学过程】

一、问题导入

A.一定 B.可能 C.不可能

师：请动动你的小脑袋思考一下，怎样选择？

生：选“可能”。因为中奖的几率很低，买10000张也可能不会中奖。

生：我也认为选“可能”。因为每一张彩票都可能中奖，也可能不中奖，所以他可能这1000 张都没中奖，也可能一两张中奖等。

揭题：可能性到底是什么呢？今天这节课我们就一起来研究它。（板书课题）

二、问题探究

1.小组活动，组织摸球，体会“可能”。

师：（依次出示一个红球、一个黄球、一个蓝球，装入同一个口袋）我把它抖一抖、搅一搅，拉紧了。现在让你任意地摸一个，你会摸到什么颜色的球？

生：可能摸到红球，可能摸到黄球，也有可能摸到蓝球。

追问：请猜想，摸到哪个球的可能性大？

生：摸到红球、黄球、蓝球的可能性一样大。

小组活动：把学生分成六个七人小组，其中每个小组摸的口袋里放一个红球、一个黄球和一个蓝球。

要求：

（1）组长拿口袋，组内成员按顺序摸球，共计摸球20 次。

（2）摸好后请把球重新放回口袋，记录员用圆片表示出摸到的球的颜色贴在黑色板子上，最后统计出结果填写到记录单上。

（3）每次摸之前，要把口袋抖一抖，用手搅一搅。

2.反馈交流，体验“可能”，六位组长依次将作品贴到黑板上。

师：在摸球的过程中，大家一定有很多体会吧？

生：我很想摸到一个蓝球，却总是摸不到。

师：的确，很多同学如愿以偿地摸到了想要的那个球，但有些同学并没有摸到。如果我想摸一个红球，能确定第几次摸到吗？

生：不能确定，有可能第一次就摸到了，也有可能一直摸不到。

生：我们组连续三次摸到了红球，我们都认为下一次该摸到黄球或蓝球了，结果却还是摸到了红球。

追问：静静地想一想，连续摸到三次红球，对下一次摸到什么颜色的球有影响吗？

（借助小组作品进行分析）

小结：在这个袋子里摸球，摸到什么颜色的球是不确定的，不确定的时候我们就说有可能。（板书）

三、问题分析

师：再来看看每个组最后摸球的结果，（板书六组数据）你又有什么发现呢？

师：是呀！刚才有同学不是猜想摸到红球、黄球、蓝球的可能性是一样的吗？这是怎么回事呢？

生：摸球的时候是有运气的，而且20 次也不能说明什么。

师：是哦，多摸几次！那我们摸120 次，每个小组，准备开始。

生：那得摸到什么时候呀！

师：那谁有好办法？生：把六个组的数据加起来不就是120 次嘛！

师：赞同他的说法吗？那我们就快速计算。（填入统计表中）

师：观察这组数据，你又有什么发现？

生：摸到三种颜色的球的次数都很接近了。

师：那摸500 次呢？想不想试试？其实，在今天这个信息技术非常发达的社会，电脑就可以帮我们完成，期待吗？

（教师打开Scratch 程序，输入500 并运行程序，产生数据并记录）

师：还想试验多少次？

生：1000 次。

师：观察这些数据，谈谈你的发现。

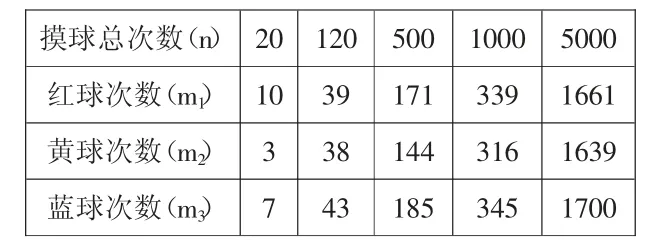
表1

生：当摸球总次数越来越多的时候，摸到三种颜色的球的次数越来越接近。

师：是呀！今天我们借助信息技术做了一件很强大的事，也验证了我们的猜想：当袋子中只有一个红球、一个黄球和一个蓝球的时候，摸到它们的可能性是相等的，是多少呢？

师：是的，其实在历史上类似于这样的试验有很多，你知道的还有什么？（抛硬币、掷骰子）老师搜集了历史上抛硬币试验的相关数据，试验结果见下表：

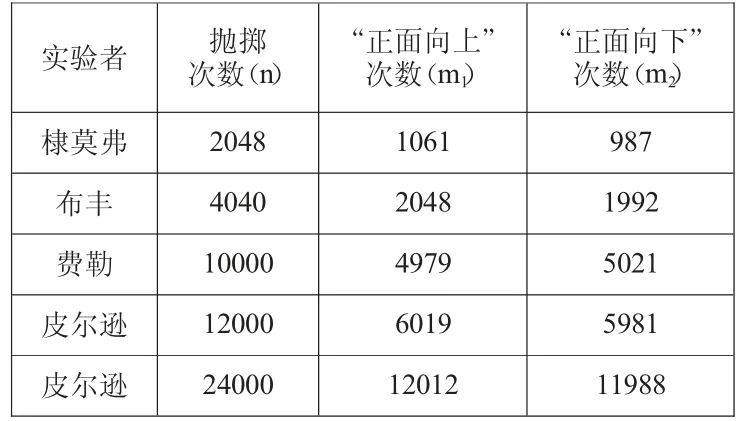
表2

师：如果我们把这些数学家的抛掷次数加起来，正面向上和正面向下的次数分别是多少？

生：抛掷总次数是52088 次，正面向上总次数是26119 次，正面向下总次数是25969 次。

师：请观察这些数据，有什么感受？

生：随着试验次数的增加，正面向上和正面向下的次数会越来越接近，也就是它们的可能性相等。

四、问题练习

1.男生女生大PK。（游戏公平吗？）

（1）游戏一：两个蓝球，两个红球，任意摸一个球，摸出蓝球男生赢，摸出红球女生赢。

师：游戏公平吗？

（2）游戏二：两个蓝球，两个红球，任意摸两个球，摸出同色的男生赢，摸出不同色则女生赢。

师：老师改变了游戏规则，但还是这个口袋，游戏还公平吗？（在练习纸上写一写，画一画）

生：我认为不公平，摸两个球，有两蓝、两红、一蓝一红三种可能，男生赢得可能性大。

生：我反对，如果两个蓝球分别是1 号蓝球、2号蓝球，两个红球分别是1 号红球、2 号红球，那女生摸到的两个球有四种可能，当然是女生赢得可能性更大。

师：两位同学到底是谁的观点更科学呢？请看大屏幕。（课件演示所有可能）现在我们都清楚地看到了这个口袋中任意摸两个球所有的可能，也就明白了女生赢得可能性比男生大。

（3）任意摸两个球，要想游戏公平，请你设计一个摸球游戏。

生：三个蓝球，一个红球，任意摸两个球，摸出同色的男生赢，摸出不同色则女生赢。

师：这样改编一下球的个数，游戏公平了吗？

生：真的可以，好厉害！

2.小军和小淇在操场上做游戏，他们蒙上眼睛在一定距离外向如图所示的边长分别为3m 和2m的正方形场地投掷沙包，掷中内圈部分小军胜，掷中外圈部分小淇胜，若未掷入大圈内则重新抛掷一次，你认为游戏公平吗？图1 和图2 你会选择哪个场地？

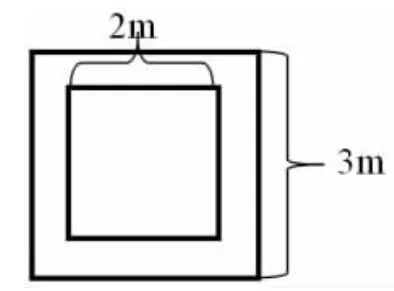
图1

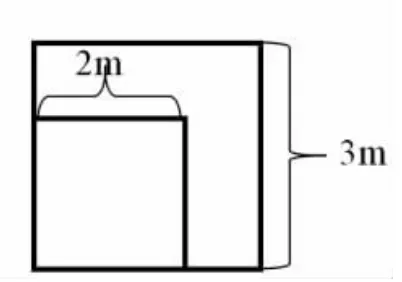
图2

生：我认为图1 不公平，因为投掷到内圈比较容易，外圈比较分散，很难掷中。图2 比较公平，掷中的可能性几乎相等。

生：我认为两个场地都不公平，外圈的面积都是5m2，内圈的面积都是4m2，明显外圈比内圈大，那掷中的可能性也是外圈比内圈大，对小军不公平。

师：同学们思考的有些道理，但数学是一门严谨的学科，游戏究竟是否公平，我们借助计算机来完成投掷试验，请组长拿出平板电脑运行程序，填写记录表。

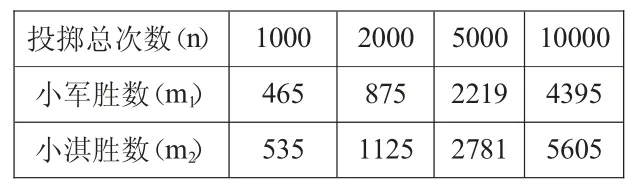
表3

师：仔细观察表3 中的数据，你有什么发现？

生：随着投掷次数的增加，小淇赢得可能性比小军大。

师：要想小军和小淇赢得可能性一样大，你会怎么设计这个场地呢？（在练习纸上画一画，算一算）

反馈：

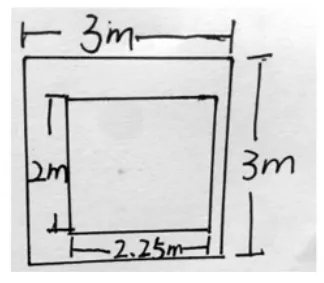
图3

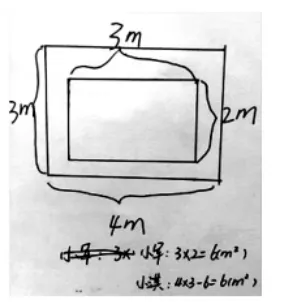
图4

五、问题回顾

师：通过这节课的学习，你有哪些收获？还有什么疑惑？

【课后思考】

课堂是缺憾的艺术。上述教学实践，虽然着力想体现《数学课程标准（2011年版）》倡导的理念：数学教学过程是教师引导学生活动的过程，让学生经历数学化的过程，让学生自己建构数学知识的过程。教师应激发学生的学习积极性，给学生提供数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。但实际操作中一定会存在许多不足，恳请各位方家批评指正！

有两点小体会，自觉得可以一提。

一、学科整合，实现思维可视化

随机现象虽然对于个别试验来说无法预知结果，但在相同条件下进行大量重复试验时，却又呈现出一种规律性，我们称之为随机现象的统计规律性。而课堂上开展试验的次数是受到局限了，想要做到像历史上的数学家抛硬币一样，有几千次或是几万次，短短的四十分钟根本无法实现。谁能代替人类完成这样的事呢？那就是计算机！笔者利用编程软件——Scratch 设计程序，程序代码简单易懂，使课堂上所有学生都聚焦于数据的变化，充分体会摸到红球次数、黄球次数、蓝球次数这三个数字的变化是随机产生的，有的学生惊叹：“你看，现在是蓝球次数最多！”过了几秒又有学生情不自禁地说：“Yeah！红球赶上来了，红球的次数最多了。”某种程度上，这样的试验激发了学生的思维能力，发展了学生的想象能力和创新意识。当试验次数从500 次到1000 次再到5000 次，学生通过数据分析感知到：随着试验次数的增加，红球、黄球和蓝球的次数越来越接近，摸到这三种球的可能性相等，课前的猜想和120 次试验后的猜想都得到了验证，学生欣喜若狂。

第二次结合Scratch 辅助教学的是第二个练习，几何概型相比于古典概型更加抽象，将抽象的随机事件做可视化处理，直观地呈现投点的全过程。学生通过平板电脑自主操作，运行Scratch 程序，输入投掷总次数，观察并分析数据，感受事件发生的随机性和统计规律性。

二、角色转换，化“操作工”为“研究者”

学生的生活经验足够支撑他们做出这样的判断：在一个装有一个红球、一个黄球和一个蓝球的袋子中，任意摸出一个球，可能摸到红球、可能摸到黄球，也有可能摸到蓝球，而且它们的可能性相等。但是学生理解的可能性相等是什么呢？即第一次摸到红球，第二次应该摸到黄球，第三次应该摸到蓝球或者连续三次摸到红球，那么第四次总该是黄球或蓝球了，而实践结果却还是红球。

显然这种认识是错误的，因此在课堂教学过程中，让学生体验摸球的过程，并把摸到的球的颜色贴出来，把结果显性化（见图5）。通过横向、纵向直观地比较，充分说明了在摸之前是不能确定摸到哪个球的，结果的出现是随机的，而前一次的摸球结果也不会影响下次的结果，从而积累对随机现象的直观感受。

图5

这节课仍然有许多地方值得再思考。比如，对于可能性，学生大都有丰富的生活经验，似乎不用教学，学生随着年龄的增长，也都能作出相对准确的判断，教材中安排此内容，教学价值和意义究竟该如何定位？还有，Scratch 程序的运用，很好地做到了学科整合，也让学生充分体验了科技的魅力，但科技是把双刃剑，是否会有学生质疑这是后台程序设计好的？高科技是否真实可信毕竟学生没有真实试验、亲眼所见。如何消除学生对高科技的疑惑倒在其次，更重要的是，如何在理性思考与现实经验之间真正建立有效的通联。