用几何的眼光看世界

王继华 刘鲜 吴向东

【摘 要】本文创建了如何结合几何来开发小学计算思维课程的新途径。即将真实世界中的物体形状抽象成几何图形，通过点线面等基本几何图形的Scratch编程和调用，自动化绘制这些形状，从而体现抽象和自动化的计算思维过程。

【关键词】计算思维;抽象;自动化;几何;Scratch编程

【中图分类号】G434  【文献标识码】A

【论文编号】1671-7384（2019）07、08-016-04

计算思维是深圳市龙岗区A-STEM教育中的一项重要内容。计算思维的关键是抽象，即对真实世界化繁为简，找到本质特征和规律，降低复杂度，建立计算设备可以处理的模型。计算思维能力强的人，抽象的能力也特别强。

由此，我们想到可以用几何的眼光看世界。世间万物在外形上虽然千差万别，但都表现出一定的基本图形，如点、线、多边形、圆形等，如旋转排列的花朵、六角形结构的蜂巢、建筑物门窗排列等等。从这些外形复杂的事物中找出基本形状及其相互之间的数学关系，就是抽象;随后通过编程，让计算机画出图形，以逼近真实的形式模拟世界万物的形状，这就是计算思维的过程。这些也是日益复杂的计算机图形学的研究内容。计算机图形学要用到很深的数学算法，但对于小学生来说，所学的数学知识相当有限，为此，我们尝试用小学数学中平面几何的浅显知识，来开发跨学科的计算思维课程。

对基本图形的抽象和自动化

小学生的认识水平和几何知识学习程度，其计算思维的学习也是相当浅显的，但这并不妨碍他们用抽象的眼光看世界，用自动化的方法去模拟真实世界，在創造中去学习。本课程依托Scratch软件，设计了如下的基本课程内容。

1.点和线

线条在生活中随处可见，其中线段是常见的一种。几何学中，线指的是点通过移动位置构成的图形，它是几何图形最基本的组成部分。

既然线是由点位移构成的，那么就可以通过编程去自动化画出线。首先，定义一个画点的积木块代码，如图1所示，这个脚本定义的点是一个出现在舞台中央位置，大小为画笔粗细的蓝色点。画线的代码如图2所示，它调用画点的积木块，移动100步，画出一条长度为100的线条。在这里，当然还有更加直接的方法，那就是不必定义画点的积木块，直接在划线的代码中实现。但作为一个好的编程代码来说，把一些基本的功能定义为积木块来调用，可以使编程结构化，这是编程的基本思想和要求。

2.面

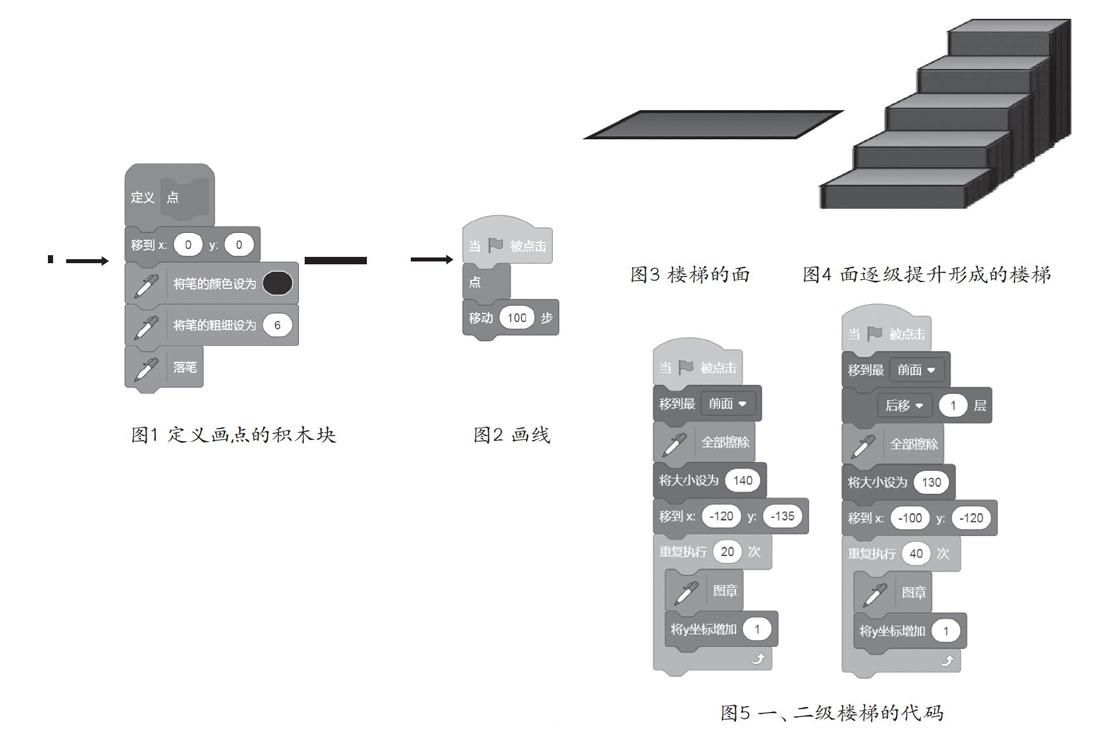
生活中的几何线条很少是单调的一条线段，它通常是以多个线条通过组合和变化形成的面出现，例如建筑物的楼梯，如图3所示。如果以面为单位，楼梯的视觉效果可抽象为由面逐级提升一定高度、缩小一定大小、并左移一定距离形成的逐渐抬高的面;为了获得更逼真的视觉效果，可以在提升面时留下痕迹，如图4。做好了这些数学化的抽象，就可以利用Scratch编程画出楼梯了（图5）。按照小学生的日常思维习惯，他们会尽量在“造型”中把图形画完备，甚至有可能有几级楼梯就画几个高低不同的方块，然后在舞台中排列，根本就不用编程。但这有违计算思维的要求：缺少抽象和自动化。再来看图5的代码，根据编程结构化的要求，还可以对代码进一步优化：一是面的绘制由自定义的积木块来完成，二是逐级提升、变小和位移的数据可以用变量来实现。这些内容可以引导学生来讨论，让他们充分感受到数学抽象和代码结构化的乐趣。

3.多边形

建筑物中常常会用到多边形元素，如三角形、长方形、六边形等，有的建筑外形中有许多正六边形。为了降低教学难度，我们把多边形都当作正多边形来对待。多边形的边即是线，线通过旋转一定的角度组成正多边形。正多边形的不同是由边长、边数和角度3个变量决定的，角度又可以通过多边形的内角和等于360°这个规律来确定，即360除以边数（这是抽象的过程）。既然如此，从编程的角度定义正多边形的边长和边数两个参数即可（图6），修改参数即可画出不同的正多边形（图7）。

自然界中还有许多复杂的形状，例如蜘蛛网，它可以抽象为多个正多边形组成的几何图形，抽象和编程自动化实现的过程如图8所示。

正多边形只是几何图形中的一种特殊形式，像平行四边形、五角星、心形和螺旋图形都是较为常见的，通过Scratch编程同样可以绘制出这些图形，不过比正多边形稍复杂些而已，也在小学生可以接受的范围。这些内容可以在学了正多边形之后，教师带领学生尽可能自主地探索。

4.圆形与弧形

圆形是真实世界中十分常见的形状，在几何图形中，圆形和正多边形关系密切，正多边形的边数越大，形状越接近于圆，以正三十六边形为例，可以推算出正多边形的边长N与圆的半径R之间的关系：N≈2πR/36≈ 0.174R。定义圆的积木块代码如图9所示，不同的圆通过组合可以形成同心圆，同心圆在生活中很常见，如枪靶，它可以通过图10的代码去模拟绘制。

除了圆形，真实世界中有还存在着有许多弧形构成的事物，如花朵、叶子、器皿等，由不同的弧形通过变形和组合构成，这些都可以通过Scratch编程来自动化实现。

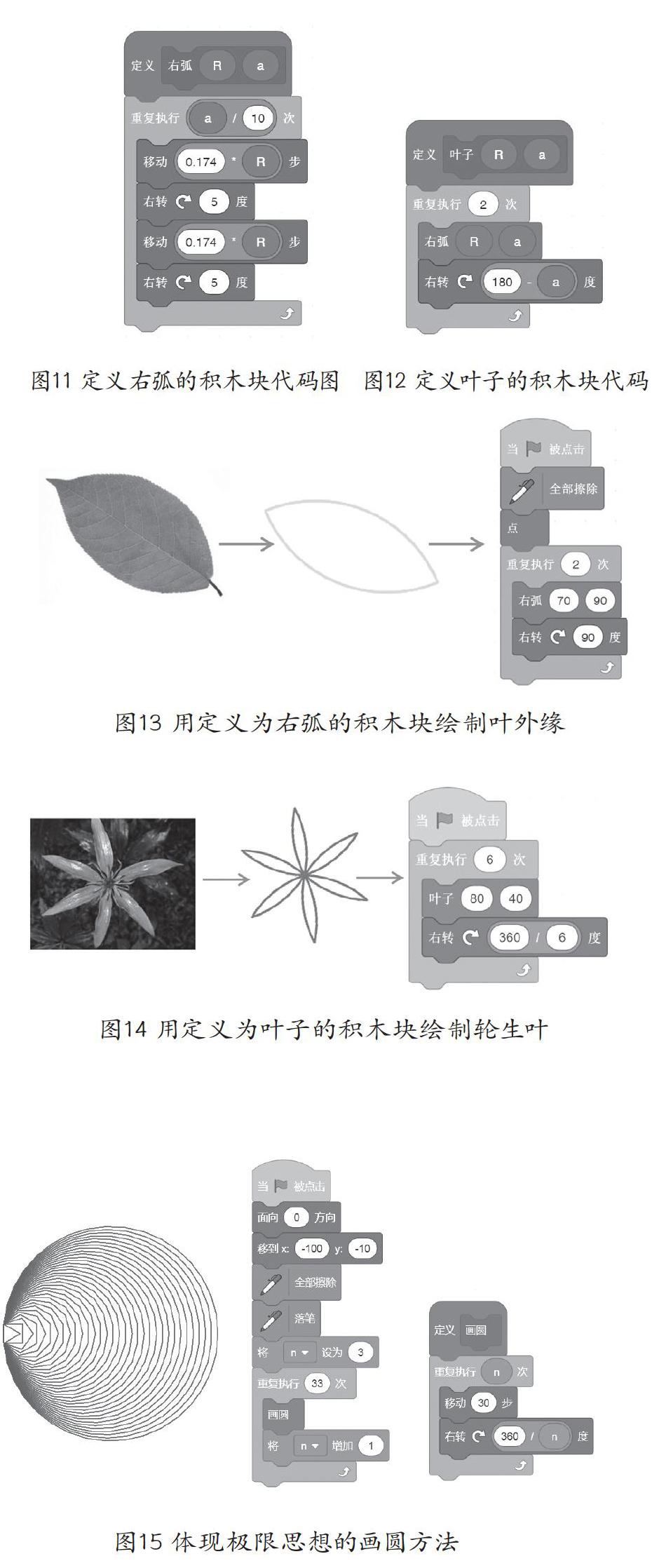
弧形可以看成是圆形的一部分，所以这里可以借鉴画圆的方法，减少重复执行的次数，即可画出弧形。因角度不同又可分为左弧和右弧，以右弧为例，定义右弧的积木块代码如图11所示。其中R代表的是弧对应的半径长度，a代表弧对应的圆心角的度数，将圆心角为a的右弧向右旋转180-a，可形成一片叶子，因此定义叶子的积木块代码如图12所示。图13所画出的叶子是由半径为70、圆心角为90°的两片右弧构成的。

通过图形探究数学

我们还试图让学生通过Scratch来探究数学，上述的例子看起来是在应用数学中的几何知识，其实也是学习几何的过程。在数学世界里，对几何形状的探究催生了新的数学思想，比如分形。要让小学生借助几何编程来探究数学是困难的，但也不是不可能。比如在绘制正多边形时，如图15，从左下角画正三角形开始，不断增加边数，当边多到一定程度时，正多边形越来越趋近于圆，这就是极限的思想。

计算思维与几何的结合有着天然的优势，特别是借助Scratch编程软件。学生在学了这些内容后，看世界的方式就不一样了。满世界都会成为有规律可循的由基本图形构成的丰富多彩的变化，这就是计算思维能力得到发展的表现，是我们最期望看到的课程学习的成效。同时，对真实世界各种事物的观察、分析、抽象和自动化实现，美育蕴含其中，使得A-STEM中有关人文的跨学科概念得到一定程度的落实，使学生在获得计算思维硬技能的同时，欣赏美、创造美等软技能也得到发展。

作者单位：广东深圳市龙岗区平安里学校  广东深圳市龙岗区宝龙学校  广东深圳市龙岗区依山郡小学