井眼轨迹计算及预测模型—分段法

(1.中国石油大学(北京)，北京，102249；2.中国石油大港油田公司，天津大港，300280； 3.北京雅丹石油技术开发有限公司，北京，102200)

引言

在石油工业中，随着井型的不断丰富，对井眼轨迹计算的准确性也提出了越来越高的要求。由于井眼轨迹的计算依赖于离散的测试点，因此如何准确判断出测点间井眼轨迹走向也就成为其中的重点。目前理论上已经有超过二十种井眼轨迹计算方法，而实际施工中常用的方法主要有平均角法、平衡正切法、校正平均角法、曲率半径法(圆柱螺线法)、最小曲率法、弦步法、自然参数法等，而由于直线或折线法本身的误差性，目前国内外普遍较为认可的方法主要有曲率半径法、最小曲率法、弦步法、自然参数法等这几种方法。

曲率半径法最开始是由Wilson等人[1]于1968年提出以上下两测点与井眼轨迹相切、并在水平与垂直方向上的投影为圆弧的假设的计算方法，之后于1987年由郑基英等人[2]提出以井眼轨迹为一段圆柱上的圆弧、且在上下两测点处与井眼轨迹垂直的圆柱螺线法，而这两种方法后被证实为同一方法。

最小曲率法是于1975年由Taylor等人[3]提出的基于空间斜平面弧线假设的计算方法，利用圆弧曲率见圆弧转化为两条直线后再进行计算。就目前应用而言，最小曲率法使用较多，但是在计算旋转导向与定向钻井的井眼轨迹时，误差依然较大。弦步法是于1986年由刘福齐等人[4]基于认为测试电缆获取的数据为井眼轨迹圆弧的弦长假设而提出的方法。自然参数法是于1995年由刘修善等人[5,6,7]提出的基于井斜及方位角变化率为常数的假设而提出的计算方法，目前已证明在计算考虑方位漂移井眼轨迹时精度较高，但由于其模型计算相对复杂，不易理解且有特殊条件，使其在现场并未被广泛应用。在现在已有井眼轨迹计算软件中基本都包含有这几类方法供现场参考使用，并且根据现场实际情况对这些模型进行改进使其能得更加精准的结果。[8-11]

本文所提出的方法与现在已有的公认较为准确的各类圆弧计算法一样，认为测点间的轨迹为一段圆弧线，分段法也是基于圆弧性质提出一种新的井眼轨迹计算方法，在圆弧假设的基础上将圆弧分成如干段，并用直线进行代替，圆弧分段越细，则各小段圆弧就越接近直线，计算井眼轨迹结果也就更精确。同时这样的方法可以应用于井筒受力之中，对井筒力学状态进行精确分析。

1 理论分析

井眼轨迹的计算通常仅依赖于多个分散的测点的数据，而由于地层因素、钻井措施等的影响，使井眼轨迹不总是规则的，因此在计算井眼轨迹时，所有的方法都对其进行了一定的假设，目前普遍接受的是各类圆弧类假设。分段法的假设条件与传统圆弧类井眼轨迹方法相似，认为相邻测点间的井眼轨迹为一段曲率为常数的圆弧(如图1)。

对于空间中的任意一段圆弧来说，其各方向上的角度随弧长的增加而成正比变化，因此对于上下测点之间可以看作是由弧长相等的多段圆弧组成，这些圆弧在各方向上的角度也由上而下呈等差数列变化。当在计算中将测点间的圆弧分成的段数越多时，这些小段圆弧也就越能看作是一条条线段，那么上下测点间也就可以看作是由多条角度呈等差数列变化的线段构成(如图2)。虽然王礼学等人[12]也对这类方法进行过探讨，但是由于其过于追求微元化，采用积分式求解，反而使模型公式出现特殊处理情况，而精度却并未得到提升。

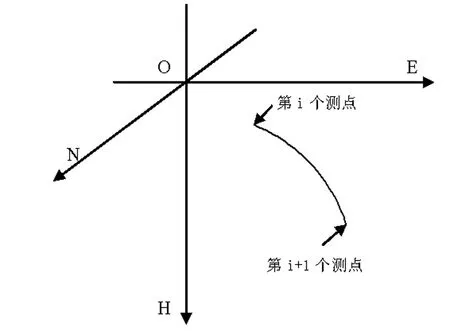
图1 某相邻两测点间井眼轨迹圆弧图

Fig.1 Trajectory arc between two adjecent testing points

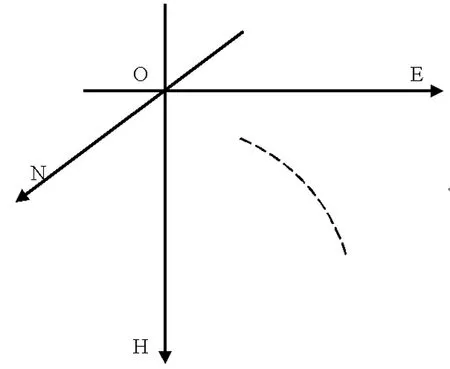
图2 某相邻两测点间井眼轨迹直线图

Fig.2 Trajectory lines between two adjecent testing points

根据以上公式可得到测点间圆弧上的每一小段的井斜角以及方位角，并以此计算出各段对应的垂深、北向及东向延伸距离，然后将这些小段进行依次叠加计算后即可得到相邻测点间的圆弧在各方向的准确延伸距离。具体计算相邻两测点间井眼轨迹数学模型如下：

可以看到当分段数n为2时，该公式即为传统的平衡正切法，但是随着分段数n的不断增大，圆弧被细分为更多更接近直线的小圆弧段，而通过利用计算机进行计算时，甚至可以将30米的圆弧分成成千上万段，从而在一定程度上得到更为精细的井眼轨迹计算结果。

在此需要指出的是：利用分段法不仅可以用来对井眼轨迹进行精确的计算分析，还可采用上一段井眼轨迹变化规律预测出下一段井眼轨迹的方位走向，同时在实际应用当中，计算结构复杂井段的井筒受力时，可以通过分段法将该段划分为小段进行计算，得到井筒受力的精确解，从而算出井筒的临界受力点所在的具体深度。

2 实例应用

为验证分段法的正确性，本文利用一口测深为3604米的井的测试数据，该井共有128个测点。分别应用目前国内外油田广泛使用的方法与分段法对该井井眼轨迹进行计算，然后对累积计算到井底的结果进行综合对比。

表1 分段法与传统方法全井段累计误差对比

Table 1 The comparison of error among Multi-interval Method and conventional methods

从上述全井段累积计算结果对比可有：在计算东向距离、北向距离时，分段法的计算结果相较于最小曲率法、弦步法的计算结果偏小，而相较于曲率半径法、校正平均角法而言的计算结果有偏大；在计算垂深时，分段法的计算结果与曲率半径法、校正平均角法完全相同，与最小曲率法计算结果在全井段深度累计误差为0.0346米，弦步法由于其假设条件上的限定使得其垂深的计算结果大于所有其他方法。通过对以上几类方法的计算结果进行对比可以看出分段法具有较好的稳定性。

同时，从结果中也可以看到，分段法与自然参数法的计算结果在数值上是完全相同的，但是在计算方法上，分段法不仅更便于理解，而且无特殊处理情况，所以在现场应用上更为简洁方便。由于自然参数法在考虑方位漂移轨道计算具有较大优势，因此，分段法也就继承了该类方法的优势。

另外，根据已有的研究结果显示，由于钻井过程中，钻进方式并非唯一不变，通常是多种钻进方式交替使用，对于不同的钻进方法，有其对应的计算误差较小的计算方法，但现场应用过程中常常仅用一种方法直接进行井眼轨迹计算分析，因此计算结果较为稳定的分段法在实际应用中效果则更优。

在井眼轨迹可视化中，与已有的各类计算方法相比，这些方法基本都只是以直线形式连接相邻两测点，这就会在一定程度上导致轨迹的失真，这种情况在造斜或降斜段表现得更为明显，又或者是需要重新进行插值计算，这样又会导致计算的复杂度增加，而分段法由于其本身的计算特性决定了其在井眼轨迹的精细化处理时更为方便、简洁。

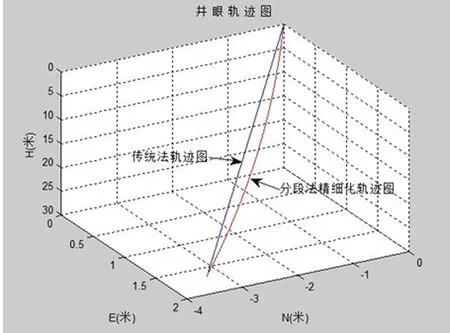
图3 分段法与传统方法井眼轨迹图对比

Fig.3 Wellbore trajectory comparison between multi-interval method and traditional method

在井眼轨迹预测方面分段法也具备较好的适用性，利用分段法将相同钻井措施段(非增斜、降斜段)的测点1与测点2之间的轨迹划分成n段计算出两点间的井眼轨迹时，可得到测点1与测点2间划分的各小段长度以及相邻两小段的角度增量为：

然后以测点2为起点继续向下进行计算，直至计算到需要预测的深度点。某井在某相同钻井措施段的三个离散测试点如表2所示：

表2 某井三个连续离散测试点数据

Table 2 The datas of three succesive discrect testing points

序号测深(m)井斜角(度)方位角(度)1778.731.72301.102807.551.58300.523836.371.54298.30

为验证分段法预测井眼轨迹的准确性，分别将根据测点2、3算出测点3在各方位上的位移量与利用分段法根据测试点1、2的数据预测出测点3在各方位上的位移量进行对比。

表3 计算与预测位移量对比

Table 3 The comparison of increments between calculated and predicted

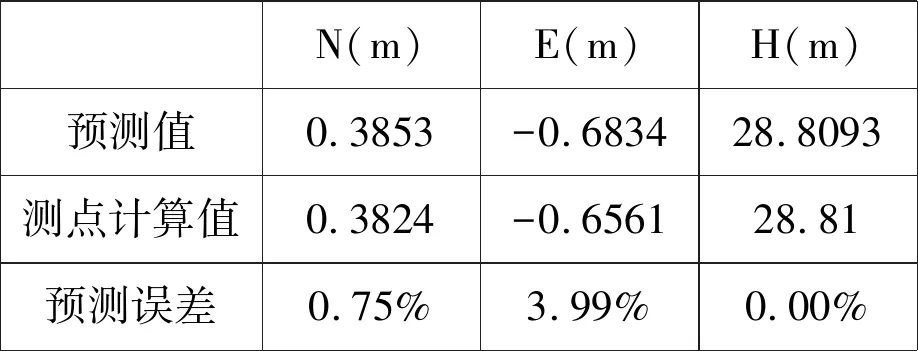
N(m)E(m)H(m)预测值0.3853-0.683428.8093测点计算值0.3824-0.656128.81预测误差0.75%3.99%0.00%

通过表3的结果对比分析可知，在利用分段法进行下部井眼轨迹预测时能够非常准确地计算出下一段轨迹在各个方向上的延伸量，其误差通常不会超过10%。因此在钻井过程中也可利用分段法为现场钻井作业的高效、精准钻进提供指导。

3 结论与展望

(1)通过对比计算结果可看到，分段法与刘修善等人提出的自然参数法计算结果是一样的，但是分段法在原理解释以及参数计算上更为简便易懂且不会出现其他特殊计算情况，无判断条件。

(2)在三维井眼轨迹描述中，分段法能够提供更为精准的轨迹。与传统的这些方法相比，在井眼轨迹三维视图中，其他方法只能提供测点间的直线走向，而分段法可根据测点间划分的各小段走向为轨迹提供更为精细化的描述。

(3)在对井眼轨迹进行与测试时，可用上一段井眼轨迹的分段步长与角度步长，然后采用分段法预测出下一段井眼轨迹。

(4)利用分段法在计算井筒受力时，可以根据需要将井筒受力情况复杂的井段划分成为比其他段更小的分段，而精确计算出某一深度处井筒的受力状态。