基于物质守恒原理的油藏渗透率时变计算方法

(中石油大庆油田有限责任公司勘探开发研究院，黑龙江 大庆 163712)

油田注水开发过程中，油藏渗透率随着注水体积倍数的增加逐渐增大[1～3]，导致渗透率变异系数、油水相渗曲线发生变化[4,5]，改变了油水运动规律[6,7]，给剩余油分布研究和挖潜决策带来困难[8,9]。因此，在油田开发过程中,需要计算不同时期的油藏渗透率，为油田开发提供决策参数和指导。目前常用的油藏渗透率变化研究方法有密闭取心井方法和测井解释分析法等[10]，但这些方法很难满足求取油藏渗透率变化率的需要：密闭取心方法是通过恒速压汞实验获得不同时间的喉道半径比，进而求取渗透率变化率，但由于取心井少，时间上不连续，而且不同时期的岩心分析数据是从不同的取心井中获得的，计算结果存在误差；测井解释分析法仅能在近井地带对渗透率进行检测描述，不能对远井地带以及整个油藏进行解释分析，空间广度太小[11]。这些方法只能代表油藏局部渗透率及其变化情况，无法给出不同时间整个油藏的渗透率变化情况。为此，笔者提出了一种基于物质守恒原理计算油藏渗透率及其变化率的方法。

1 计算方法

1.1 渗透率时变数学模型

渗透率与喉道半径的关系式为[12]：

(1)

式中：K为油藏渗透率，mD；r为喉道半径，μm；f1、f2分别为喉道因子和孔隙度因子，均为常数。

由式(1)可得油藏开发任意时间的渗透率与原始渗透率和喉道半径关系的数学模型为：

(2)

式中:Kt为油藏开发t时间的渗透率，mD；K0为油藏原始渗透率，mD；rt为油藏开发t时间的喉道半径，μm；r0为油藏原始喉道半径，μm。

由式(2)可得到油藏开发t时间的渗透率变化率ΔKt为：

(3)

1.2 喉道半径比的确定方法

由式(2)可以看出，只要知道原始渗透率和喉道半径比，由渗透率时变模型就可以计算得出油田开发t时间的实际渗透率。原始渗透率是已知的，关键是如何确定喉道半径比。油藏开发过程中，采出液中会伴有颗粒物质，这是由于喉道内的矿物质受到注入水的冲刷，随注入水一起被采出，导致喉道半径扩大，喉道体积增大。认为采出水总悬浮物泥沙体积基本上与增加的喉道体积相等，由此得到喉道半径比，计算出渗透率变化率。

在理想情况下，假设油藏中全部喉道是由n个单位长度为L、半径为ri的喉道组成的，则全部喉道体积V为：

(4)

式中：ri为喉道i的半径，μm。

由式(4)可得喉道半径比与喉道体积比的关系为：

(5)

将式(5)代入式(2)便可求出油藏开发t时间的渗透率。

2 应用实例

X区块含油面积6.97km2，地质储量为0.16×108t，原始油藏体积为1.95×106m3，油藏原始孔隙度为28.5%，油藏原始孔喉比为35，平均渗透率1145mD，开采目的层为葡Ⅰ油层组,油层埋藏深度970.4～1126.2m，原始地层压力为11.34MPa，地层破裂压力为13.3MPa，油层温度为46℃左右，平均砂岩厚度为19.9m，1965年投入注水开发。

2.1 渗透率及其变化率的时变计算

统计了X区块1988～2015年的年产水量和水中悬浮物含量，以1988年、1996年、2001年、2003年、2013年和2015年数据为例，如表1所示。

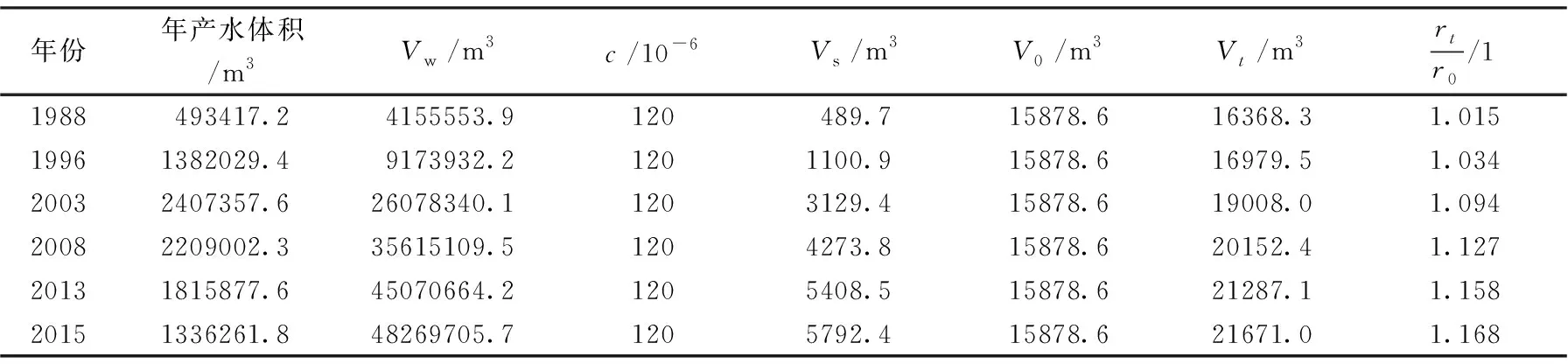
表1 X区块不同时间的喉道半径比计算结果

表2 X区块的渗透率及其变化率

表3 喉道半径比计算结果与室内试验结果对比

年份喉道半径比/1计算结果室内试验结果19881.0151.01420081.1271.12120131.1581.15

将表1数据代入式(2)得到X区块的渗透率Kt，将Kt和K0代入式(3)得到X区块的渗透率变化率ΔKt，计算结果如表2所示。

2.2 渗透率变化计算结果与室内试验结果对比

X区块内有连续的密闭取心井，将计算的喉道半径比与室内恒速压汞试验测量的喉道半径比进行对比(见表3)，结果表明，利用笔者计算方法得到的结果与室内试验结果高度相符，能够准确计算出油藏渗透率及其变化率。

3 结论

1)建立了渗透率时变关系数学模型。根据渗透率与喉道半径关系建立了渗透率随开发时间变化的时变关系模型。

2)建立了喉道半径比时变关系数学模型。根据采出水总悬浮物泥沙体积基本上与增加的喉道体积相等的关系建立了喉道半径比随开发时间变化的时变关系模型。

3)计算了X区块的喉道半径比、渗透率及渗透率变化率。计算的喉道半径比与室内恒速压汞试验结果高度相符，为油藏渗透率的变化研究提供了一个新的技术手段。