考虑不完美排错和检测率下降变化的软件可靠性模型

徐 立

(1.中国科学技术大学 苏州研究院， 江苏 苏州 215000;2.商丘职业技术学院 软件学院， 河南 商丘 476100)

在现代市场中,产品质量决定了企业能否在激烈的竞争中生存下来[1]。软件产品作为一种特殊的产品，在发布和交付使用前，需要对软件的可靠性进行预测和评估，以避免发布和交付后昂贵的修复代价。预测和评估软件的可靠性是预测软件尚有多少没有被测试出并修复的bug。该问题看似简单，但并不容易解决，因为除了已测试出的bug这个随机不确定事件外，没有更多数据可以依赖。如果能依赖已测试出并修复的bug按照某种规律建立一个自适应和鲁棒性强的预测模型对软件可靠性进行预测，则将极大提升软件可靠性，具有重要的研究意义。

1 相关工作

通过对以往可靠性模型的文献进行梳理发现：模型是基于非齐次泊松过程(NHPP)，且假设bug检测率是常量，bug强度正比于剩余bug量，或bug检测率是一个增长函数变量。例如，经典G-O模型[2]虽然是后续研究的重要参考和比对对象，但假设条件和实际情况相差较大，实际情况是bug检测率并非常量或增长函数变量，而是一个下降的函数变量，因为大的、危害严重的bug更容易在早期被检测出。开发和测试人员的经验也表明，测试出的bug检测率随着测试时间的推移会越来越低，通俗的说，在后期测试出bug会更加困难。

除此之外，一些研究为了更好地建模，会将bug检测的过程假设为完美的过程，即检测出的bug在修复时不会引入新的bug，但实际情况并非如此，往往是开发人员在修复bug时会引入新的bug，即排错过程是不完美的。因此，在建模时考虑排错过程的不完美性更具有实际意义。最早考虑不完美排错过程的软件可靠性模型是Pham模型[3],Pham考虑了测试人员的学习因子并认为bug检测率与尚未被检测到的bug成正比。Jha等[4]考虑了不相关bug所占比例的因素，提出了一种不完美软件可靠性模型。Ahmad[5]提出了基于指数分布的不同bug总数函数的不完美调试软件可靠性模型。Zhang等[6]在建模时融入测试资源的花销因素，提出了不完美调试软件可靠性模型。 Zhang等[7]把bug总数函数看作是测试时间的函数，同时考虑到排错过程会引入新错误，提出了不完美排错可靠性模型。虽然这些考虑不完美排错的软件可靠性模型能够有效地应用在一定的测试环境中，但是bug修复过程中引入的复杂性导致这些模型不能完全应用到其他测试环境中。

本文考虑了不完美排错和检测率下降变化的因素，提出了一种软件可靠性模型(IDDD soft reliability model)。同其他模型相比，所提出模型具有更好的拟合和预测性能：

1) 考虑了不完美排错和检测率下降变化的因素，提出了具有更好的拟合和预测性能的软件可靠性模型；

2) 提出的bug总数函数是一个非线性变化的函数，且排错时bug引入的数量具有非线性变化的特征，能提升可靠性模型的质量。

2 IDDD软件可靠性模型

2.1 相关约定

为了方便描述模型及推导过程，使用的模型相关缩略语和符号说明如表1所示。

表1 模型相关缩略语和符号说明

2.2 模型基本假设

软件可靠性模型建立的公共假设条件如下：

1) 在软件测试过程中，bug检测和修复过程服从NHPP；

2) 软件失效发生是由软件中剩余bug造成的；

除公共假设条件外，模型其余假设条件包括：

3) bug检测率随测试时间呈逐渐下降变化；

4) 每次检测出的bug立即被修复， 新的bug可能被引入且bug总数函数随测试时间非线性变化。

2.3 模型提出及推导过程

本文中使用的符号含义参见表1。NHPP表示为：

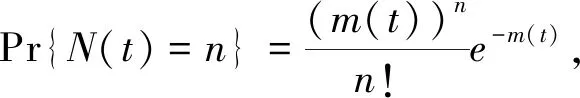
n=0,1,2,…

(1)

根据假设2)建立微分方程，见式(2)。

(2)

式(2)表示当前检测出的bug数量和软件中剩余bug数量相关。为方便建模，一般假设b(t)为常量，即当前检测出的bug数量和软件中剩余bug数量成正比。

根据假设3)得到bug检测函数，见式(3)

(3)

根据假设4)，a(t)可以表示为

a(t)=a(1+αtd)

(4)

式(4)表示最终检测出的bug总数量由软件中最初期望检测出的bug数量和bug引入数量组成，且引入bug的数量随测试时间非线性变化。

将式(3)(4)代入式(2)，得到式(5)。

(5)

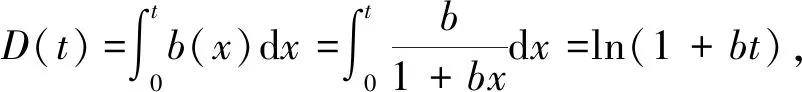
(6)

(7)

将式(4)代入式(7)，得到

(8)

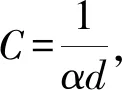
(9)

式(9)即本文提出的软件可靠性模型。

3 实验

3.1 数据集

实验设计选取2个常用数据集用于评价和对比IDDD模型的预测性能和拟合性能。一个数据集是文献[8]中的实时控制系统的失效数据；另一个数据集来自于Tandem计算机系统[9],共包含4个软件产品发布的bug数据集，每个数据集分为两部分：① 用于模型拟合和参数估计的部分(前9或7条失效数据)；② 模型预测性能比较的部分(剩余的失效数据)。

3.2 评价指标

选用3个公认的评价指标评价模型的性能。评价指标见式(10)～(12)。

(10)

其中n是总的观察出的bug数量。

AIC=-2log(likelihood function at

its maximum value)+2N

(11)

其中N表示模型参数的数量。

(12)

式(10)用于评价模型的拟合性能，SSE值越小拟合性能越好[9]；式(11)用于评价模型的预测性能，AIC值越小，则模型的预测性能越好；式(12)用于评价模型的拟合性，其值越接近1，拟合性能越好[8]。

3.3 实验结果

文献[7,9-10]提出的模型为考虑了不完美排错因素的可靠性模型，与IDDD模型在数据集1上用SSE和Rsquare两个指标进行拟合性能对比。由于3个对比模型中的参数估计采用了最小二乘法，因此IDDD模型也采用最小二乘法进行参数估计，对比结果见表2。

表2 模型拟合性能比较结果

文献[11-12]中，Zhang和Wood认为P-Z模型和G-O模型在同其他模型比较时具有最好的预测性能，因此，本文选取这两个模型与IDDD模型进行比较。由于要使用AIC指标，参数估计采用极大似然估计法。在4个软件产品bug数据集上的比较结果见表3～6，其中G-O和P-Z模型的实验结果来自文献[11],验证了结果的正确性。

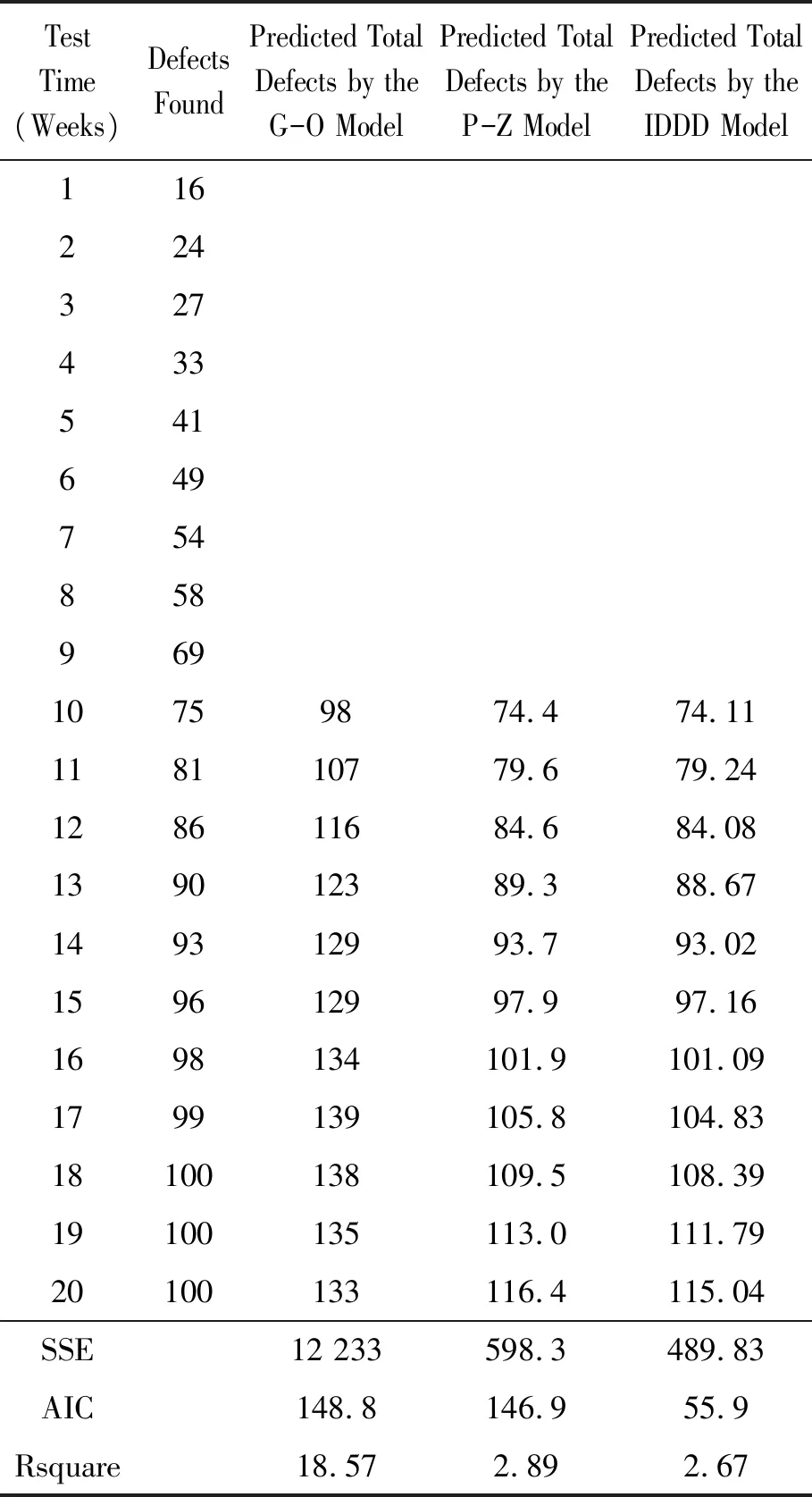
表3 使用第1款软件产品bug数据集时IDDD与G-O、P-Z的比较结果

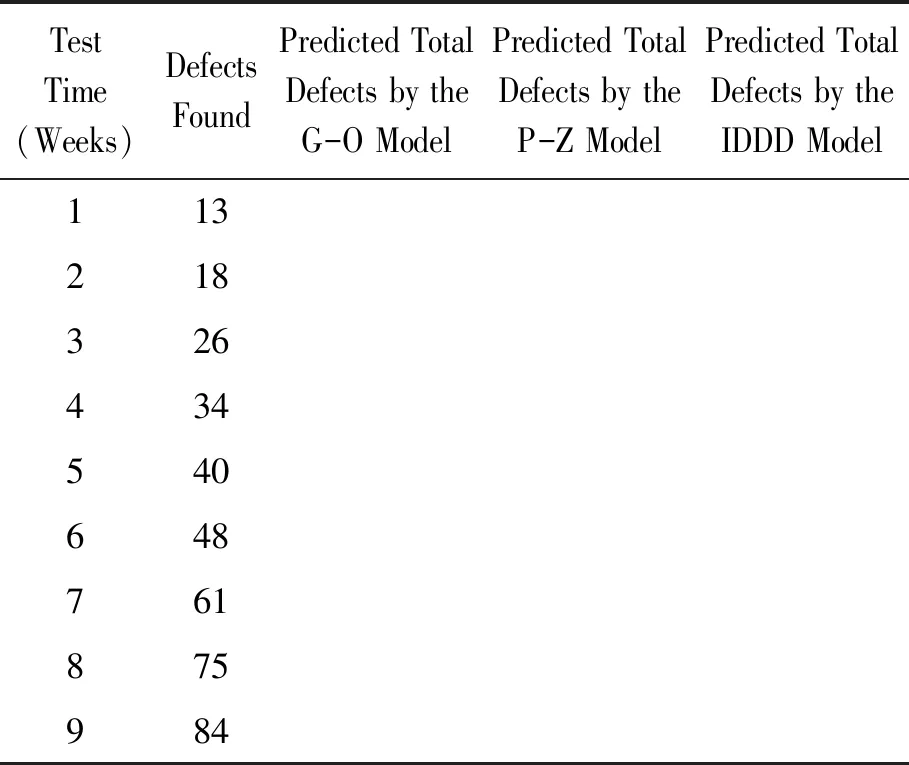
表4 使用第2款软件产品bug数据集时IDDD与G-O、P-Z的比较结果

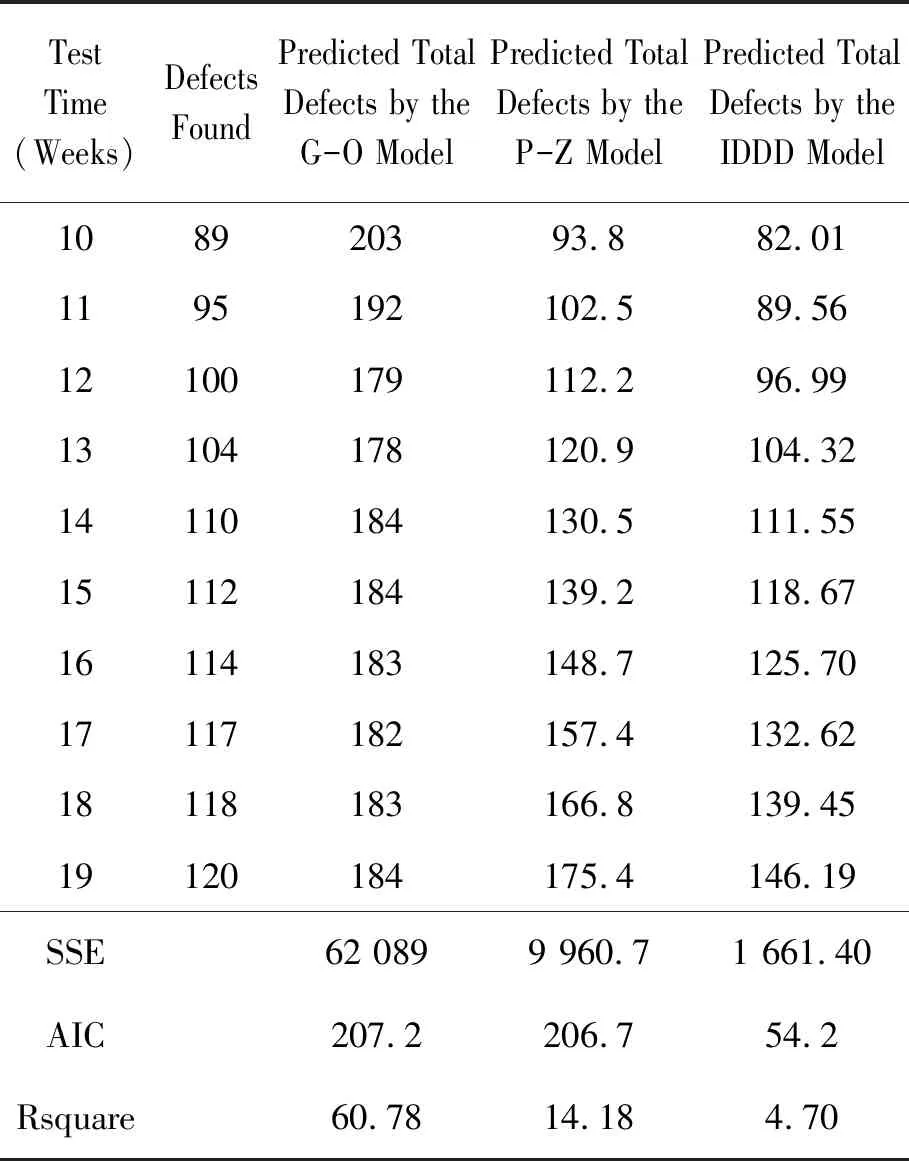
续表(表4)

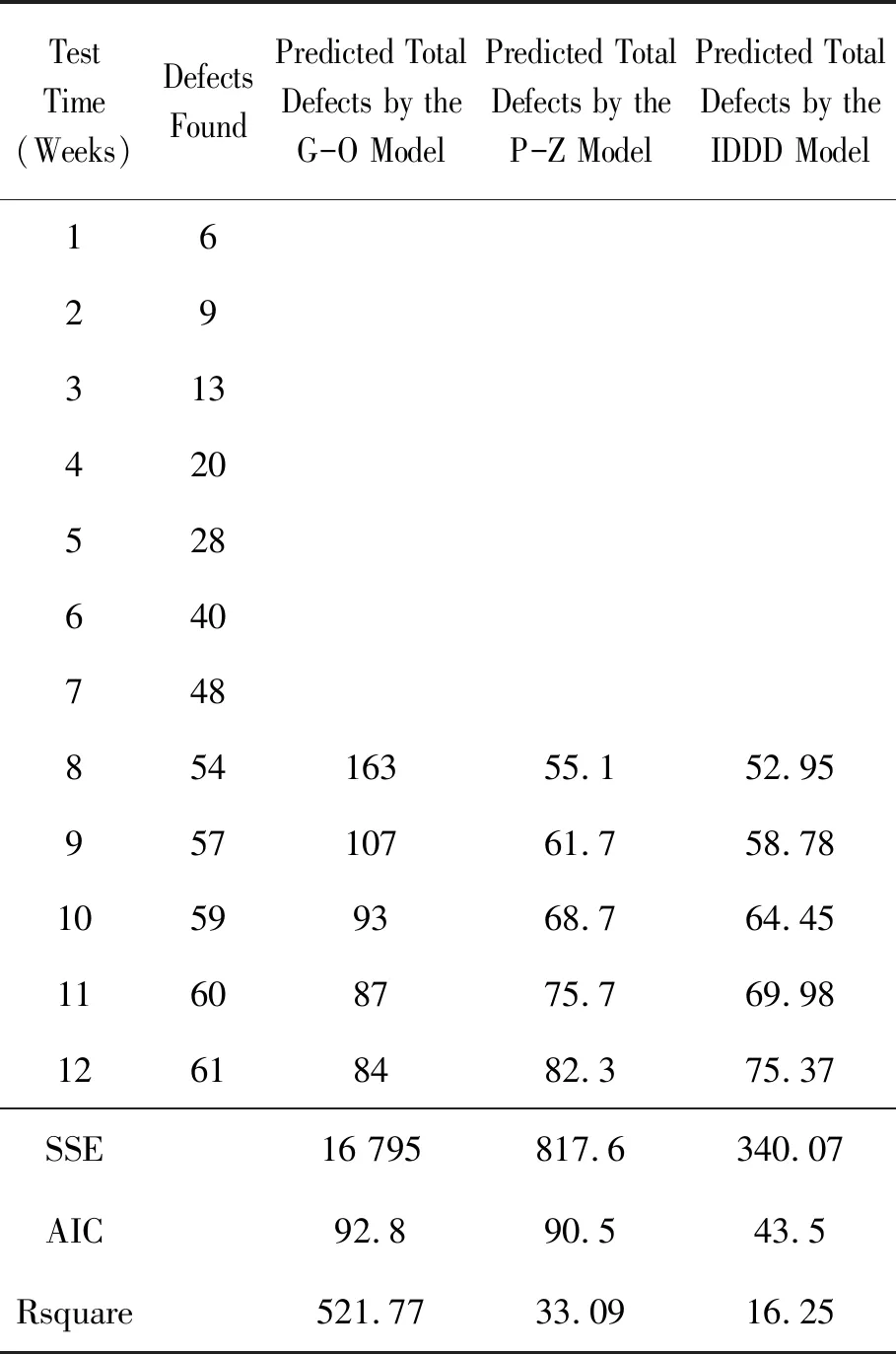
表5 使用第3款软件产品bug数据集时IDDD与G-O、P-Z的比较结果

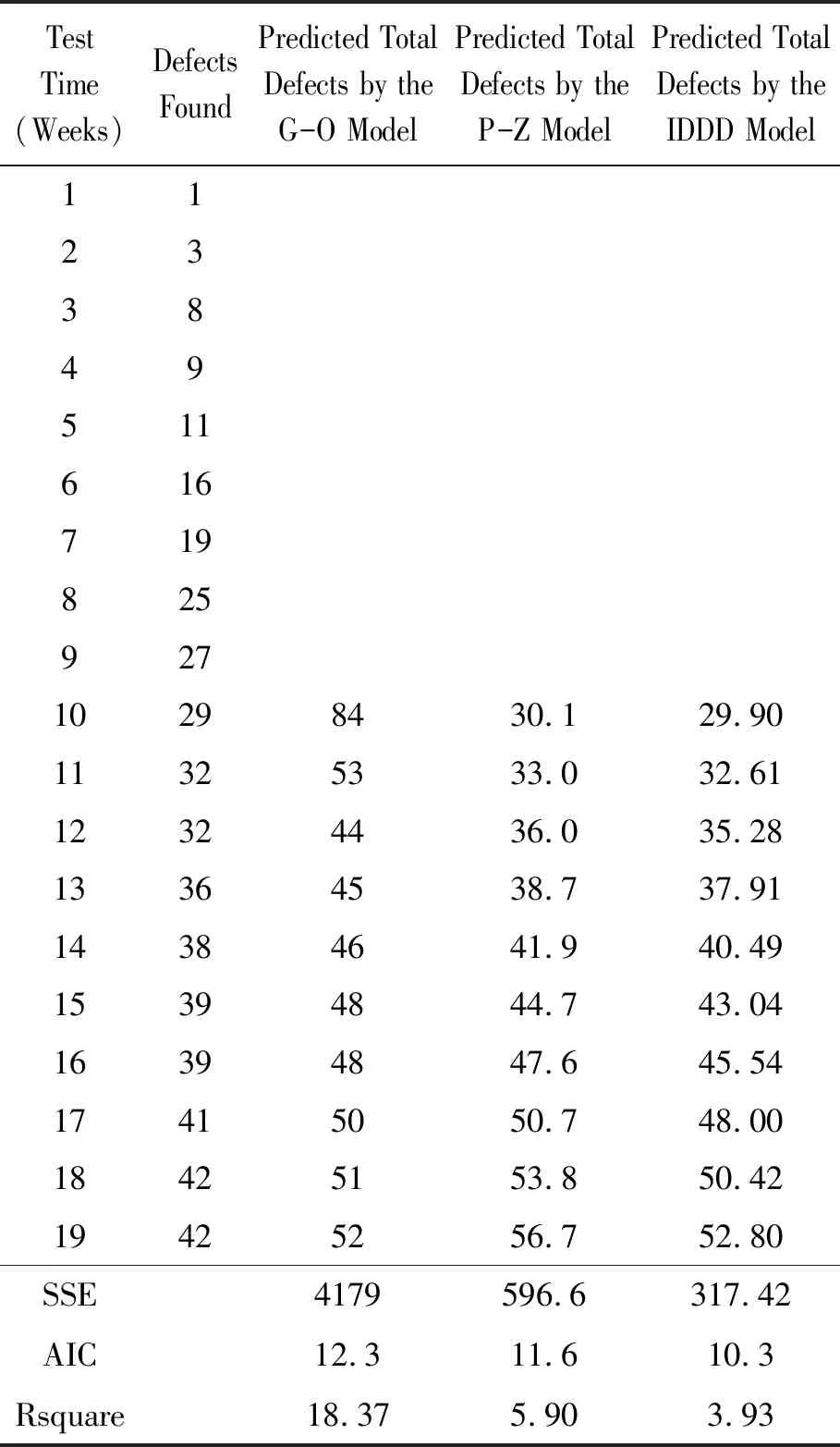
表6 使用第4款软件产品bug数据集时IDDD与G-O、P-Z的比较结果

3.4 实验结果分析

从数据集1上IDDD模型与3种考虑不完美排错因素的模型的比较可以看出：IDDD模型的SSE和Rsquare指标明显优于模型1和模型2，略优于模型3,尤其Rsquare的指标达到了0.999,说明拟合性较好。在数据集2上，IDDD模型与G-O模型、P-Z模型对比主要使用了SSE和AIC两个指标，同时也计算了3个模型的Rsquare指标。需要说明的是，与在数据集1上的实验结果相比时，Rsquare指标看似表现较差(表3～6中Rsquare值与1相差较大)，这是由于用于模型拟合的失效数据过少(只有7条或9条失效数据)，两者不具有可比性。在表3中，G-O模型的SSE和AIC值是IDDD模型的25倍和2倍多，P-Z模型的SSE值与IDDD模型接近，但AIC值是IDDD模型的3倍。表4中，G-O模型的SSE值和AIC值分别约为IDDD模型的37倍和4倍。表5中，G-O模型的SSE值和AIC值分别为IDDD模型的5倍和2倍，P-Z模型的SSE和AIC均超过IDDD模型的2倍。表6中，G-O模型和P-Z模型的AIC值与IDDD模型相近，但SSE值分别为IDDD模型的10倍以上和近2倍。表3～6中，IDDD模型的Rsquare值也优于G-O模型和P-Z模型。由此可见，IDDD模型的预测性能明显优于G-O模型和P-Z模型。分析IDDD模型表现优秀的原因如下：

1) 提出的模型建立在bug引入为非线性变化的假设之上；

2) 提出的模型建立在bug检测率随测试时间有下降的变化趋势的假设之上；

3) 提出的模型整合了上述两种假设的bug检测率。

4 结束语

本文提出了一种考虑bug检测率具有下降变化的不完美调试的软件可靠性模型，假设bug引进随测试时间为非线性变化。采用经典的bug数据集、3个模型比较标准、2个普遍认为有较好预测性能的模型和3个考虑不完美排错的模型进行对比来评测模型的性能。实验结果显示，所提出的模型有较好的拟合和预测效果，并能更准确地预测剩余bug的数量。假设具有下降趋势的bug检测率和非线性变化的bug引进更符合实际的bug检测和去除变化情况。因此，本文提出的模型能更有效地在实际软件测试中预测软件中剩余bug的数量。

另外，该模型虽然被设计用来预测软件可靠性，但对于符合故障检测率呈下降趋势和不完美排错规律的硬件产品[12]或设备[13]，也可尝试作为一种辅助预测工具。