基于CEEMDAN-SSA 的MEMS 加速度计振动噪声抑制方法
闫 琦,杨冬梅,张凤云,武彦君,张建红
(北方自动控制技术研究所,太原 030006)
0 引言
倾角传感器为系统提供被测物体的姿态信息,已广泛应用于航天、国防等领域。近年来,随着MEMS 技术的发展,采用MEMS 加速度计制成的倾角传感器凭借其体积小、响应速度快、精度高等特点在倾角测量中得到广泛应用。在载体发动机振动的条件下,MEMS 加速度计的输出信号受到振动噪声影响很大,从而影响姿态解算精度。
本文在文献[1-5]的研究基础上,提出采用基于自适应噪声的完全集合经验模态分解和奇异谱分析相结合的方法,来抑制载体发动机振动噪声对MEMS 加速度计的影响。首先利用CEEMDAN 方法,可以将MEMS 加速度计测量信号分解成若干瞬时频率有意义的固有模态函数(IMF),保留残余分量,利用模态相关准则将信号层和噪音层分开,并对信号层中的IMF 分量进行奇异谱分析去噪,将去噪后的重构信号与CEEMDAN 分解得到的残余分量合并得到去噪后的加速度信号。使用这种方法既能改善EMD 方法模态混叠的问题,又能避免直流分量对奇异谱分析的影响。经过实验数据分析,这种算法可以有效地保留加速度计信号的能量和特征,并且大大降低振动噪声对加速度计测量结果的影响。
1 基本原理
1.1 CEEMDAN 方法
CEEMDAN 方法的核心是经验模态分解方法。黄锷在1998 年提出的经验模态分解方法(EMD,Empirical Mode Decomposition)[6],是一种非稳态、非线性信号自适应时频分析方法。然而当信号存在噪声干扰时,EMD 方法发生的模态混叠现象将严重影响分解效果。为了克服这一缺点,总体经验模态分解方法(EEMD,Ensemble Empirical Mode Decomposition)[1]被提出,通过在原始信号中加入不同的白噪声,使得信号在不同尺度上具有连续性,减少频谱混叠现象。但是EEMD 重构序列中存在残留噪声,每次需要选择不同幅值的白噪声。
在EEMD 的基础上,Torres M E 等[7]提出带自适应白噪声的完全集合经验模态分解(CEEMDAN,Complete Ensemble Empirical Mode Decomposition with Adaptive Noise),通过对加入的白噪声进行EMD 分解,代替每次加入白噪声的过程[8],可以自适应地添加噪声,减少重构序列残留噪声。
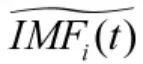
1)CEEMDAN 方法对信号x(t)+ε0nj(t)进行M次分解,εi表示附加白噪声与原信号的信噪比。分解的第1 个模态分量为:
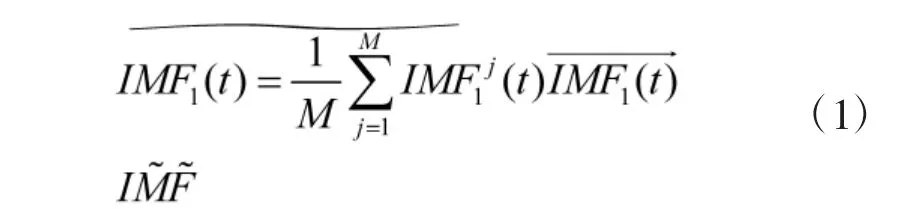
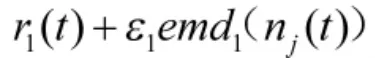
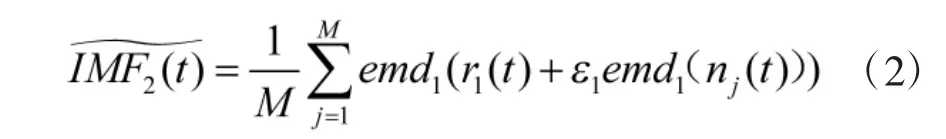
4)继续用2)的方法进行计算,得到第k+1 个模态分量为:
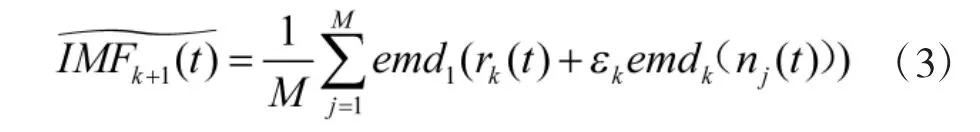
5)将k 的数值加1,返回第3)步,当残余分量满足迭代终止条件时停止分解,此时原始信号表示为:

这种方法可以提供一个原信号完整的重构。
1.2 奇异谱分析(SSA)
Colebrook 在1978 年第1 次提出了奇异谱分析方法(SSA,Singular Spectrum Analysis),该方法是对一维时间序列进行分析的主成分分析法。这种方法可以将平稳或非平稳的原始信号分解成许多互不相关的信号之和,这些信号可以被解释为原始信号的趋势、周期及非周期的噪声。这种方法的主要原理如下[2]:
对于采样信号的时间序列x(i)(i=1,2,…,N),可以构造如下的Hankel 矩阵:

这里需要设定适合的窗口长度M,得到的轨迹矩阵为M×K 阶,其中,K=N-M+1。


分组可以分离信号中的加性成分,将轨迹矩阵Hi的下标{1,2,…,d}分成两大类HI和HI'。

其中,HI代表原序列中前p 个有用组分,HI'是原序列的残余序列,其中,I={i1,i2,…,ip},而HI占原序列的权重为
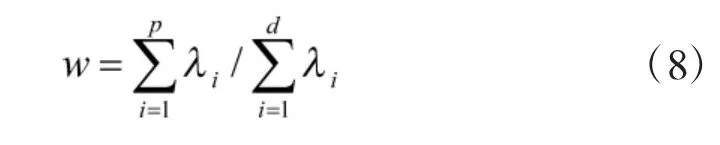
2 CEEMDAN-SSA 方法
CEEMDAN 方法根据自身的时间尺度特征将信号分解为有限个本征模态函数和一个余项之和,这种方法可以将高频噪声很好地分离出来,但随着分解层数的增加,可能会产生虚假分量,对信号的低频部分无法得到良好的分解效果。而SSA 方法可以将信号分为互不相关的信号之和,选择合适的序列重构以达到处理信号的目的,然而对于含有直流分量较强的信号,使用SSA 方法不能正确地选择有效秩阶数,有效地分量信号和噪声。
基于这两种方法各自的优点,选择将这两种方法结合的CEEMDAN-SSA 降噪新方法。
这种方法的主要步骤如图1 所示。
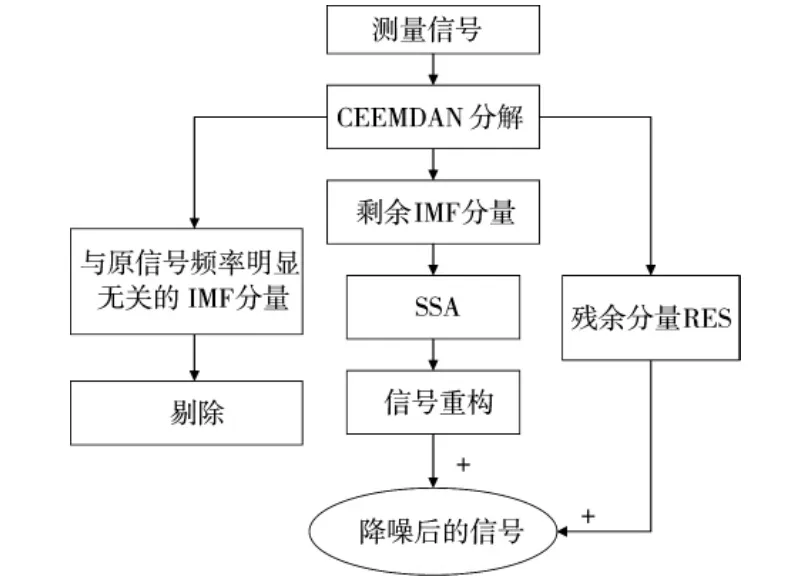
图1 CEEMDAN-SSA 方法流程图
1)对待处理的含噪信号进行CEEMDAN 分解,得到频率从高到低排列的本征模态函数IMF 和残余分量res。res 是一个趋势项,表示信号的平均发展趋势。研究发现,趋势项会对奇异谱分析的准确度造成影响,并且趋势项一般频率较低,认为其不含噪声,所以保留残余分量res。
2)根据EMD 模态相关的分选准则[3]分离与原信号频率明显无关的IMF 分量,判定信号层和噪音层。模态相关的分选准则由计算模态函数与测量信号之间的互相关系数决定,表示为:

3)将剩余的IMF 分量使用SSA 方法进行降噪处理,按照原信号的特点进行重构。
4)将重构信号与步骤1)得到的残余分量相加,获得降噪后的信号。
3 实验数据分析
本实验使用的是MTS2001 型双轴倾角传感器,它是由两个互相垂直的MEMS 加速度计组成。忽略温度对MEMS 倾角传感器影响,分别测试某轮式车底盘发动机开启和关闭的情况下,载体平台上MEMS倾角传感器内部加速度计敏感表头的输出结果。每次测试时间1 min,采样频率为400 Hz,信号带宽5 Hz。
首先对振动噪声信号进行初步分析。图2 分别展示了在加速度计静止状态下发动机开启和关闭时位于y 轴的加速度计的实验结果。从图2 中明显看出,在发动机开启的状态下,加速度计输出受到了振动噪声的干扰,有用的加速度计信号已被淹没,这种情况将严重影响倾角传感器的测量精度。
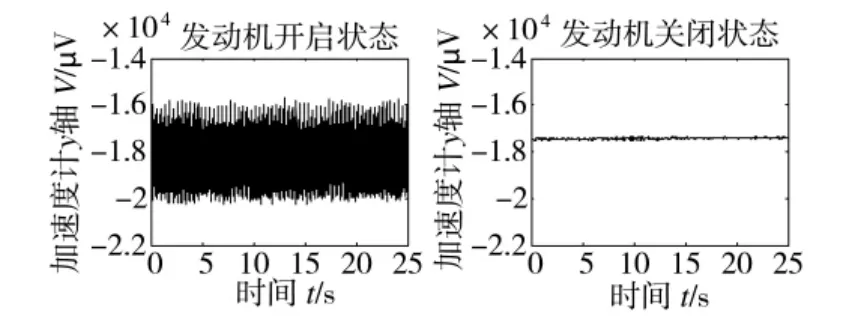
图2 加速度计在发动机开启和关闭状态下的输出结果
将载体平台小幅度转动,获得的有用信号淹没在噪声里,需要进行滤波去噪的处理。为了降低振动噪声的干扰,提高测量精度,截取一段长度为10 000的数据序列,使用本文提出的方法进行数据处理。
首先,使用CEEMDAN 方法将加速度计信号序列分解为不同时间尺度,添加的白噪声幅值系数k=0.1,实现次数为M=500,分解结果如图3 所示。
测试信号经过CEEMDAN 分解得到了12 个模态函数和1 个残余分量。从图3 中可以看出,CEEMDAN 方法使频谱混叠问题得到了很好的改善。IMF 分量从上到下波动性逐渐变小,说明各IMF分量的频率越来越低。残余分量的幅值比其他各IMF 分量的幅值大很多,同时明显表示了信号的变化趋势,保留res 分量。
计算各IMF 分量与测试信号的相关系数,图5中画出各IMF 分量与测试信号的相关系数的计算结果。如图所示,IMF5 集中了大部分的噪声信号,对应于图5 中幅值最明显的17 Hz 附近。而相关系数局部最小值出现在第9 个IMF 分量处。由模态相关准则方法可以得出,将前9 个IMF 分量作为噪音层剔除。

图4 相关系数曲线图

图5 奇异值占比图
剩余的3 个IMF 分量频率较低,但仍需考虑低频噪声对信号的影响。将这剩余的3 个IMF 分量进行奇异谱分析去噪,并对IMF 分量进行重构。设置SSA 算法中的时间窗口M=400,构造Hankel 矩阵,对矩阵进行奇异值分解得到奇异值谱,图5 是前50个奇异值每阶奇异值的占比图,从图中可以得到,前2阶奇异值包含了信号90%以上的能量,从第3阶开始,曲线趋于一条直线,可以认为这部分为信号的噪声部分。故选择2 为重构阶数,得到降噪后的信号。将降噪后的3 个IMF 分量与残余分量相加得到降噪后的加速度计信号。
图6 是加速度计x 轴实测数据和使用本文方法处理后的结果,从图中看出,经过CEEMDAN-SSA方法处理后,加速度计输出数据得到了明显的改善,经过处理后信号保留了信号的变化趋势,同时明显降低了振动噪声对加速度计输出信号的影响。
为验证方法的有效性,分别使用EMD 方法和SSA 方法对测试信号进行处理,将这两种滤波方法与本文提出的方法进行滤波结果对比。为对降噪效果进行定量说明,通常选择信噪比(SNR)、均方根误差(RMSE)作为性能指标评价滤波效果。SNR 越大,RMSE 越小,说明该方法的去噪效果越好。

图6 加速度计小幅度转动去噪前后曲线图
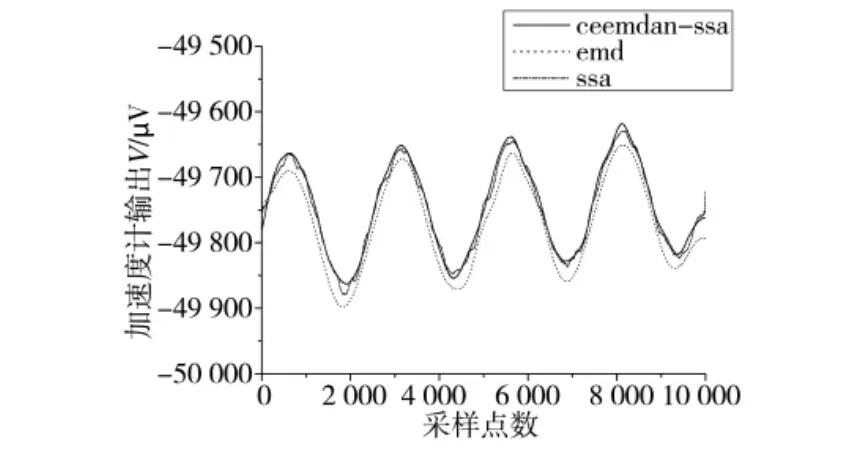
图7 3 种方法滤波效果对比图

表1 3 种方法滤波效果评价指标比较
图7 是分别使用这3 种方法对测量信号进行滤波处理的结果对比图,表1 是通过滤波性能指标来比较这3 种方法的效果。从图中可以看出,这3种方法都大致恢复了原信号的主要特点,但是使用经验模态分解的处理结果恢复的信号所含能量较低,这可能受EMD 方法频谱混叠的影响,在分解过程中发生能量损失,使滤波后的重构信号相对原始信号失真较大,表中显示使用EMD 方法后均方误差最大。而图中明显可以看出,由于直流分量的影响,使用SSA 方法滤波后的重构信号所含噪声较大,曲线的平滑度不如其他两种方法,表中显示使用SSA 方法的信噪比最小。用本文提出的CEEM DAN-SSA 方法滤波后信噪比最高,均方误差最小,能够证明这种方法的有效性。
4 结论
本文针对MEMS 加速度计测量时受到载体发动机振动噪声影响的问题,提出了一种基于CEEM DAN-SSA 的降噪方法。这种方法结合了CEEMDAN和SSA 方法的优点,由于加速度计的有效信号集中在低频段,首先使用CEEMDAN 方法保留信号的主要趋势项,使用模态相关准则分离信号层和噪音层,然后对信号层进行SSA 处理,根据奇异值的占比选择重构阶数,重构后与CEEMDAN 分解的残余分量相加,得到降噪后的信号。通过对实验数据的处理和其他处理方法的对比,证明了该方法的有效性。虽然这种自适应噪声完全集合经验模态分解具有分解完整性、模态精准性等优点,但同时存在运算效率低的问题,需要进一步完善。

