减涡管出口角度对去旋系统特性影响数值模拟
郝媛慧,王锁芳,夏子龙
(南京航空航天大学航空发动机热环境与热结构工业和信息化部重点实验室,南京210016)
0 引言
现代航空发动机需要非常高的循环温度来提高运行效率,因此高压和低压涡轮主流通道的气体温度是相当高的,需要二次空气系统提供高压气流对盘腔和机匣进行冷却、封严。为降低气流在压气机盘径向内流动造成的压力损失,常采用减涡器结构。目前其形式多为管式、去旋喷嘴式和导流板式。其中管式减涡器流动特性简单,易于设计,但在高转速下存在振动、破裂的风险。Peitsch等[1]对管式减涡器的研究模型基于2种减涡管安装方式,并与1维计算做对比,得到较好的一致性。Negulescu等[2]对去旋喷嘴式减涡器和管式减涡器旋转腔的压力损失特性展开了试验和数值研究,结果表明管式减涡器流动特性简单,易于设计,但易振动;无管式减涡器机械上优于管式,但其流动呈非单调特性,存在瞬态迟滞响应行为。Pfitzner等[3]试验分析了应用于BR700系列发动机上的管式、无管式减涡器设计参数对流动特性的影响。Hide等[4]对旋转腔内源汇流场进行等温分析,提出流动由4个区域组成,并指出流动主要由切向速度做主导。Wormley[5]在狭窄的腔体实验中观察到类似的流体状态。Du等[6]对导流板式减涡器进行数值模拟,重点研究了导流板与径向的夹角及导流板曲率变化对质量流量与压力损失的影响。吴丽军等[7]研究了管长、鼓筒孔形状及不同进口速度对管式减涡器流动损失的影响。廖乃冰等[8]数值模拟了有无导流盘引气的盘腔内部流场,分析了二者的速度场、压力场。呼艳丽等[9]利用试验方法测出带去旋喷嘴的盘腔流动阻力,并对共转盘内的流场分布进行了数值研究,发现共转盘内的压力损失受去旋效应和旋转效应共同影响。王远东等[10]通过试验研究了不同工况、参数等对带导流板的旋转盘腔内部流场的影响。武亚勇[11]通过试验和数值模拟研究对比了去旋进气的大尺寸共转盘内部流场。陈阳春[12]同样对带去旋的转动盘腔流动换热进行了数值模拟,发现相同条件下对转盘换热效果比转-静盘好。张光宇等[13]对共转盘腔径向内流进行了数值模拟,并分析了不同转速下喷嘴结构变化对盘腔流场结构的影响。单文娟[14]对比了直管式与弯管式减涡器的流场特性,分析了90毅弯管及与转轴成一定角度时对压力损失的影响。而弯管出口法线与径向之间的夹角变化对压力损失的影响未见文献报道。
本文基于文献[14]提出的导流管减涡器对减涡管出口选取4种角度变化,针对共转盘腔径向流动展开数值模拟,获得不同出口角度对盘腔内流场结构和减涡器去旋减阻性能的影响规律。
1 物理模型和计算方法
1.1 几何模型和网格划分
选取鼓筒孔入口、旋转盘腔、导流管、主流道的腔体空间为研究区域。计算域几何模型如图1所示。减涡器有15根减涡管,在轴向对称分布,则在周向取24毅扇形区域(即计算模型中含有1个减涡管对应4个进口)建模。为研究减涡管出口角度琢对计算结果的影响,琢分别取30毅尧60毅尧90毅。无量纲参数见表 1。所有计算模型为非结构化网格,通过改变第1层边界层网格尺寸以保证壁面Y-Plus位于30~300之间。
在转速为9380 r/min下进行网格独立性验证,如图2所示,确定网格总数为150万左右。
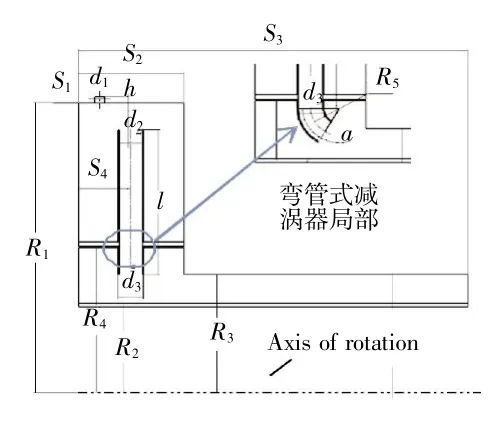
图1 管式减涡器主要几何尺寸
1.2 数值方法及验证
采用 Fluent商用软件,基于压力稳态求解器,计算域均为旋转域,采用标准壁面函数,选取Realizable资-着模型,该模型与资-着模型相比采用了新的湍流黏度公式,着方程是从涡量扰动量均方根的精确输运方程推导出来的,在雷诺应力上保持与真实湍流一致,在旋转流计算中得到的结果更符合真实情况[15]。文献 [1]的计算模型与本文类似,得出的Realizable资-着紊流模型更适合求解此类流动,且本文出发点并非是选取、分析湍流模型。
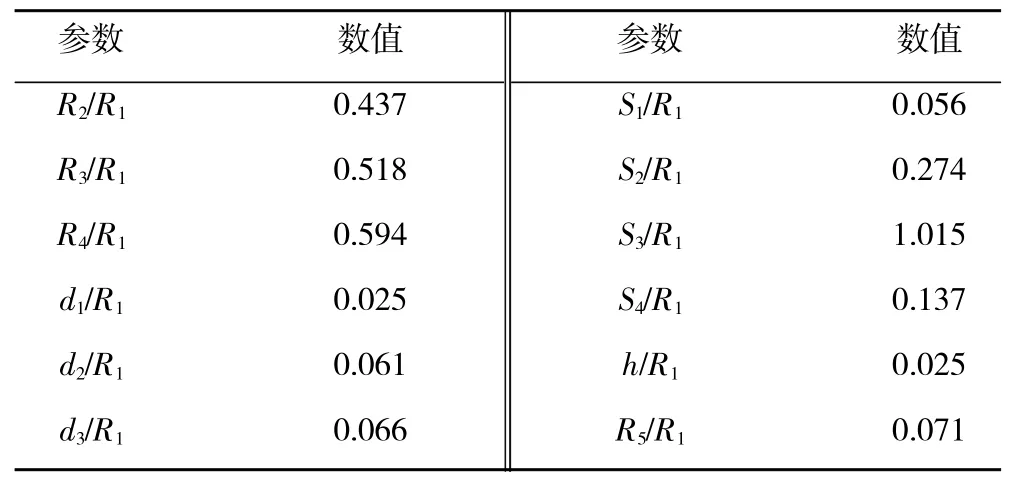
表1 无量纲参数
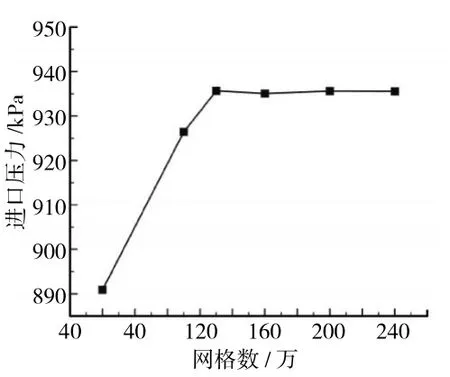
图2 网格独立性验证
1.3 边界条件
进口采用流量边界条件,流量设置为1.248 kg/s,总温为620 K,出口采用压力边界条件,静压设置为810.6 kPa,计算工况转速为 7380、9380、11380 r/min。
1.4 参数定义
旋流比

式中:V兹为周向速度;棕为旋转角速度;r为当地半径。
旋转雷诺数

式中:籽为空气密度;滋为气体动力黏度。
总压损失系数

2 计算结果及分析
2.1 流场分析
在转速为9380 r/min时、x=0截面的盘腔流线如图3所示。图中均为垂直纸面向外旋转。从图中可见,在相同转速下,所有导流管进口处流线类似,流场大致相同,这是由于导流管出口角度变化导致下游流场结构发生的变化对上游进口流场结构所产生的影响较小。进入导流管的气流流体基本为径向流动,未进入导流管的气流在导流管两侧呈不同流动状态,如图4所示。从图中可见,导流管左侧由于进气孔的原因气流径向速度较大,受到切向哥式力作用,射流切向速度增加,对盘腔内流体造成扰动,产生1对方向相反的涡;导流管右侧气流径向速度较小,以切向速度为主,并向低半径方向发展。从图3(a)中可见,射流直接冲击轴,在滞止区的高压推动作用下形成壁面流动,并在两侧出现大小相近的漩涡,此外在哥式力和离心力的作用下,使得径向流动进一步受阻,从而流动方向发生显著改变;从图3(b)中可见,气流受导流管约束,其流向发生偏折,仍然存在冲击射流效应,在出口流向偏折处产生较大漩涡,而在另一侧漩涡较小,大漩涡气流很难突破,受到挤压,增加了压力损失;从图 3(c)中可见,气流偏折角增大,与图 3(b)的类似,在出口流向偏折处两侧分别产生一大一小2个漩涡,且2个漩涡尺寸差异加大,大漩涡随着流向发展;从图3(d)中可见,出口气流接近轴向,出口处漩涡消失,但气流仍然有径向分速度,在远离弯管出口处会对轴有一定冲击,并产生1个小回流。
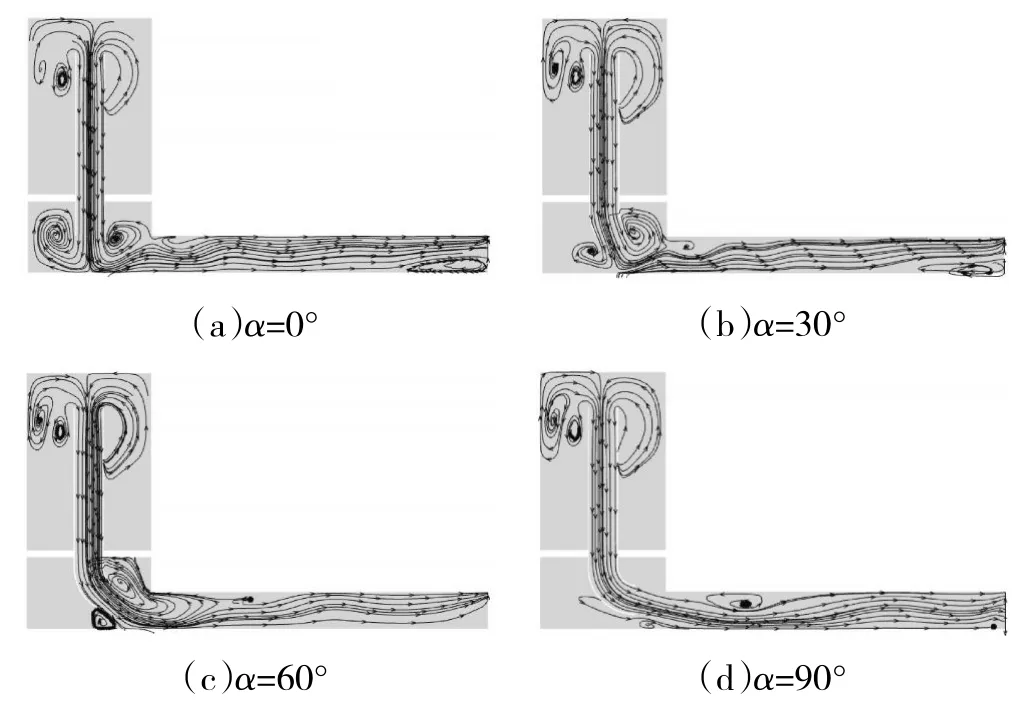
图3 x=0截面盘腔内流线

图4 进气孔出口流线
4种结构的旋流比Sr在导流管及导流管进口的分布是一致的,如图5所示。从图中可见,当气流进入盘腔后,由于需要克服沿径向向外的离心力和哥式力作功要大于转盘对其的作功,总压不断减小,从进气孔出口到导流管入口,Sr略大于1,表示该半径处气流的切向速度大于转盘的切向速度,气流对转盘作功,在导流管中心Sr接近于1,而在壁面处由于摩擦力的作用,Sr略小于1,表现为转盘对气流作功,使气体总压增大。在导流管出口,图 5(a)、(b)、(c)的情况类似,Sr大于1,并且沿着轴向先增加后减小,并维持在1.2~1.3范围内,最后在出口附近减小至0,这一过程中总压也在降低。图5(d)所不同的是气流在导流管出口后Sr仍然维持在1左右,只有局部增大,最后同样在出口附近减小至0,利于气流向下游流动,而总压损失也比前3种的小。
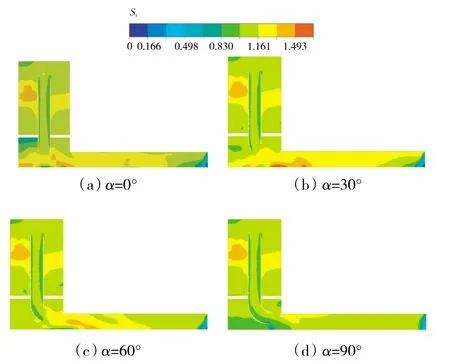
图5 x=0截面旋流比
2.2 流动损失分析
从进口到出口的总压损失系数Cp用于衡量安装该导流管的共转盘腔的总的压力损失。导流管出口角度分别为 0毅尧30毅尧60毅和 90毅的计算模型在旋转雷诺数为 2.13×106、2.71×106和 3.28×106下的盘腔压力损失分布如图6所示。在3种雷诺数下,随着导流管出口角度变化,总压损失系数Cp所呈现的变化趋势是一致的,直管式与60毅弯管式的压力损失非常接近,30毅弯管式的压力损失最大,而90毅弯管式的压力损失最小。这是因为30毅弯管式导流管出口处有较大漩涡,气流难以突破,冲击射流损失仍然较大,再加上在出口弯管处产生的局部损失,二者之和比起直管对轴的冲击射流所产生的压力损失还要大,因此图中30毅弯管式比直管式的总压损失系数高。增大出口角度,虽然出口处仍有漩涡,但由于气流偏折角的增大,气流流通顺畅,冲击射流损失减小,因此60毅弯管式总压损失系数减小,当出口角度为90毅时,气流接近轴向,出口处的漩涡基本消失,此处的冲击射流损失很小,因此总压损失系数进一步减小。
由此可见,导流管出口角度在 60毅耀 90毅之间对于降低压力损失是有优势的。
在所有转速下,压力损失随出口角度的变化分布均存在1个最高点,此处压力损失最大,因为该模型出口弯曲度仅为30毅,气流偏折方向不大,但由于出口弯度使得气流流出时不能均匀分向两侧,在主流方向一侧和反方向一侧分别产生一大一小2个漩涡,气流受到的扰动大,流动不均匀,因而在降低对轴的射流冲击损失上影响较小,再加上弯管处的局部损失,总的压力损失较大,从而表现出该模型的压力损失最大。表示的是出口弯管的局部损失与冲击射流损失之和由大到小逐渐减小至小于直管射流冲击损失的过程。
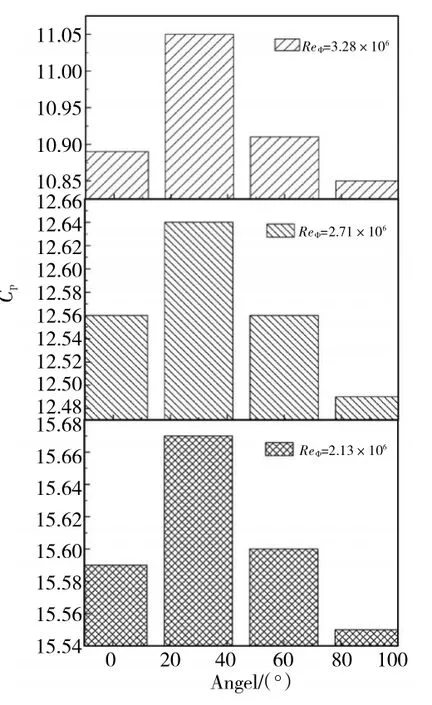
图6 盘腔和导流管的总压损失系数
3 结论
本文通过对不同出口角度下的管式减涡器开展数值模拟研究,得出各模型压力损失随转速的变化规律,得到如下结论:
(1)在相同转速下,直管式与60毅弯管式减涡器降低压力损失的效果相近,90毅弯管式降低压力损失的效果最好,30毅弯管式降低压力损失的效果最差。
(2)在所有转速下,压力损失随出口角度的变化分布存在1个最高点,此处压力损失最大。
(3)在所选工况下,增加转速,总压损失系数总体减小。

