基于拓扑优化的曲边轮廓锯齿叶冠结构设计
苑 旺 ,申秀丽 ,董少静
(1.北京航空航天大学能源与动力工程学院;2.先进航空发动机协同创新中心:北京100191)
0 引言
现代航空航天用燃气涡轮发动机的涡轮转子叶片常采用锯齿形阻尼叶冠[1-2]。相邻叶片的叶冠抵紧后可以减小叶片的扭曲变形和弯曲变形,增强叶片的刚性[3]。但是叶冠的使用也带来一些问题:叶冠位于涡轮转子半径最大处,在高转速下,对叶根和轮盘产生较大的离心载荷[4];叶冠本身也会发生故障[5-7];PSM公司R.Seleski等[8]研究了一系列叶冠掉角故障后,提出在叶冠结构形式设计中可以考虑将尖角部分切除,且为了平衡重心和考虑到各个尖角掉块的可能,对叶冠的4个角均进行切除。
为了减小叶冠对叶根和轮盘产生的负荷,减少叶冠掉角故障发生的几率,通过切除部分叶冠的方法减轻叶冠的质量是1种可行方案[9]。白忠恺等[10]对锯齿冠进行简单切除,计算表明可以有效降低叶冠局部的最大应力;Nirmalan等[11]对气冷叶片叶冠处的换热进行试验研究,发现叶冠的边角部位主要靠中心部位冷却后再以导热的方式对其冷却,若能去除这些边角部位,叶冠的冷却效率将得到提高。虽然采用这种结构的叶冠可以带来应力、冷却等方面的优势,但是这种结构的叶冠会对涡轮级的气动效率产生影响[12]。Pfau等[13]研究这种曲边轮廓的锯齿冠提出,通过合理设计可以保证涡轮转子的气动效率;贾惟等[14]的研究表明,叶片排上、下游压比和径向间隙才是影响叶冠泄漏流动的主要因素。
国内外对锯齿冠的轮廓设计均开展了一些研究:国内的锯齿冠修形设计通常是对出现故障的叶冠进行局部修改,设计后叶冠合理性通常通过试车进行考核[7];国外主要研究切除部分结构的叶冠对换热效率和气动性能的影响[15],对于改善叶盘结构的应力水平和锯齿冠形状改变后对减振特性的影响少有涉及。随着航空航天燃气涡轮发动机转速的不断提高,叶盘结构承受的离心载荷不断增大,合理设计叶冠形状从而改善叶盘结构应力水平,分析各种锯齿冠的改进改型设计,在原有锯齿冠上如何切除合适的部分,曲边轮廓的锯齿冠对叶冠减振特性影响的研究亟待开展。
本文对典型涡轮叶片的叶冠进行拓扑优化,采用有限元计算评估优化后的叶冠对叶盘结构静载荷下应力水平以及对减振特性的影响。
1 锯齿冠拓扑优化
1.1 叶冠轮廓优化方法
通过切除部分叶冠的方式来达到减重以及改善叶盘结构应力水平的目的,切除的方式是通过拓扑优化的方法在叶冠上表面确定合适的切除线,然后将2维的切除线拉伸为柱体对叶冠进行切除得到曲边轮廓的锯齿冠。根据实际锯齿冠的设计情况,给出切除原则如下:
(1)保留接触部分。接触部分是叶冠发挥阻尼作用的关键部位,相邻的叶冠之间相互接触而互相抵紧,从而改善叶盘结构的振动特性;
(2)保留篦齿部分。篦齿可减少漏气,提高涡轮的效率;
(3)切除线尽量避免曲率大的线条。研究发现,若叶冠轮廓线局部曲率过大,在这些部位会出现应力集中,从而导致掉块现象,不利于叶冠可靠工作和保持寿命[16];
(4)切除后叶冠需包裹叶尖型面及其与叶冠的倒圆。虽然文献[8]中也出现了带翻边叶冠结构的叶片,在没有充分的证据证明这种结构不影响气动效率的前提下,暂不考虑;
(5)尽量保持叶冠重心位置不变。这样可以尽可能减小由于叶冠结构调整对叶身造成的附加扭矩及弯矩。
1.2 叶冠轮廓拓扑优化
叶冠的3维结构(带部分叶身)如图1所示,相邻叶冠的接触面如图2所示(图中黑色部分)。根据上述切除原则,基于ANSYS Work-bench的拓扑优化,锯齿冠拓扑优化区域如图3所示。从图中可见,黑色部分为锯齿冠轴向2个端面拓扑优化区域,得到优化后(静强度计算时给出具体载荷和约束)的叶冠如图4所示。拓扑优化得到的叶冠边界是3维的复杂曲线,考虑到叶冠实际制造与加工情况,这里采用2维切除线切除,边界经修复与光顺处理前后的模型如图5所示。

图1 叶冠的3维结构(带部分叶身)

图2 相邻叶片的接触面
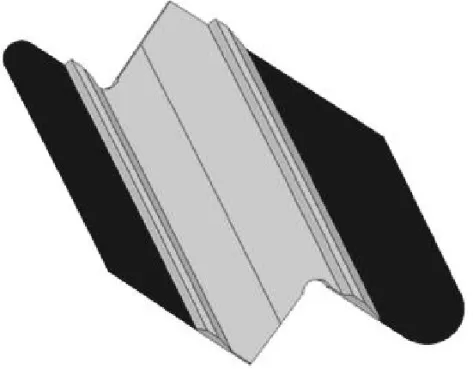
图3 锯齿冠拓扑优化区域

图4 锯齿冠拓扑优化结果

图5 锯齿冠拓扑优化前、后对比
叶冠拓扑优化的数学模型为[17]

式中:ei为设计变量,表征结构中的单元,取值为0或1,取值为0时代表删除单元,取值为1时代表保留单元,最终得到的e表征当前结构较原结构删除/保留单元的情况;P为无量纲目标函数,优化目标为使结构质量最轻、刚度最大;Vd为结构体积,Vd,i和Vd,0分别为当前和初始结构总体积;1/ln(SE)d为结构刚度,结构刚度越大,在受力时抵抗弹性变形的能力越强,在激振力作用下的振幅越小,其中(SE)d,i和(SE)d,0分别为当前和初始结构总应变能;(滓max)r为第r个应力约束所表示的最大值;(滓*)r为第r个应力约束所表示的许用值;sr为相应应力下的安全系数。
从图5中可见,优化后的锯齿冠相对于原叶冠多了许多折转的区域,少了一些尖角区,叶冠侧边的平直轮廓变成了曲边轮廓;可以从叶冠的轮廓看出叶尖叶形;封严篦齿以内的叶冠部分保持原有的形式。
典型锯齿冠拓扑优化后,经修复的最终模型去除了优化区域60.6%的体积,整圈叶冠质量降低了31 g,去除部分的质量占叶片质量的2.4%。优化后的叶冠质心偏移0.3 mm,其中,周向向叶背方向偏移0.17 mm,轴向向前缘方向偏移0.26 mm,径向向中心方向偏移0.01 mm。
2 锯齿冠优化前后静强度对比
2.1 边界条件设置及网格无关性验证
对叶冠优化前后的叶盘结构采用有限元计算进行强度分析:原始模型由叶片、轮盘、挡片组成。挡片与叶片、轮盘之间均有接触,主要作用是限制位移,将以相应的位移约束代替挡片结构。将整圈叶盘模型按照叶片数m进行分割,取1/m进行计算分析。叶盘结构的计算模型如图6所示。

图6 计算模型(经变形处理、榫接作遮挡处理)
叶片材料为某铸造高温合金,轮盘材料为某锻造高温合金,计算中所涉及的叶片和轮盘材料参数分别见表 1、2。

表1 叶片材料参数

表2 轮盘材料参数
设置约束和载荷:设置轮盘前安装边轴向位移为0;设置榫槽与榫头轴向相对位移为0代替挡片的约束;榫槽与榫头之间的接触模式设置为bonded;设置转速20000 r/min代替离心载荷;考虑到叶冠工作面的挤压应力和预扭应力的影响,叶冠边界条件采用叶冠法向位移协调并施加装配预紧力[18],叶冠装配预紧压力为40.3 MPa,施加在叶冠接触面上。
网格无关性验证分析见表3。从表中可见,采用10节点的四面体单元,考核点为静载荷下叶盘结构最大Von-Mises应力。经计算,不同网格尺寸下叶盘结构应力分布相同,最大Von-Mises应力位置均位于盘心处,且最大网格尺寸计算结果相较于最小网格尺寸的相对误差小于1%,故可使用表中coarse网格尺寸进行有限元计算,但进行拓扑优化时,由于需要得到精确轮廓,故需选择细密的网格。

表3 网格无关性验证
2.2 叶冠优化前、后关键部位应力对比
叶冠优化前、后关键部位应力对比结果见表4。表中滓web为辐板处最大径向应力;滓de为盘心处最大周向应力;辐板和盘心位置如图6所示;滓bs、滓bt分别为叶身与上、下缘板连接处最大Von-Mises应力,其位置分别如图7中A点、图8中B点所示;滓z为叶冠“Z”形凹口处最大Von-Mises应力,其位置如图9中C点所示。

表4 叶盘结构关键部位应力对比

图7 叶身与叶冠转接处
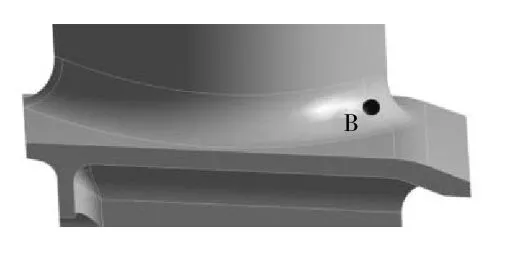
图8 叶身与缘板转接处

图9 锯齿冠“Z”形凹口处
叶冠优化后,辐板处最大径向应力滓web降低0.4%,盘心处最大周向应力滓de降低0.7%,由于切除的质量有限,优化后的叶冠对于降低轮盘应力水平有一定好处,但是效果不明显。
在带冠叶片结构中,叶身与上、下缘板的连接处容易产生应力集中,有时会导致叶片断裂[19]。叶身与上、下缘板连接处结构分别如图7、8所示。从图中可见,叶身与上、下缘板连接处的厚度变化较大,且曲面形式较为复杂,易产生应力集中。
进行静载荷下应力计算,提取叶身与上、下缘板连接处的最大Von-Mises应力。从图7、8中可见,叶冠经优化后叶身与上缘板连接处的最大Von-Mises应力滓bs降低16.1%,且最大Von-Mises应力位置由叶背转至叶盆;叶身与下缘板连接处的最大Von-Mises应力滓bt降低5.6%,相比于叶身与下缘板连接处,叶身与上缘板连接处的最大Von-Mises应力降低更多,这是因为叶身与下缘板连接处过渡更平缓且距离叶冠较远,故叶冠质量变化对该处应力的影响较小。
叶冠工作在高温高转速的恶劣环境中,即使应力小于屈服应力,也有可能发生蠕变,导致“Z”形凹口处裂纹的产生(如图9所示),使叶冠失效[20],故分析研究锯齿冠轮廓优化前、后叶冠“Z”形凹口处应力十分重要。
叶冠优化前其Von-Mises应力在叶盆方向“Z”形凹口处(图9中C点)达到最大值506.76 MPa,优化后该处最大Von-Mises应力为382.40 MPa,降低24.5%。优化前、后叶冠部分Von-Mises应力对比如图10所示。

图10 优化前、后叶冠部分Von-Mises应力对比
优化后的叶冠对于辐板和盘心处的应力影响较小,对于降低叶身与上、下缘板连接处Von-Mises应力水平收益较大。由于与叶冠距离等原因,叶冠质量的减小对于降低叶身与叶冠连接处Von-Mises应力的大小影响更显著。优化后的叶冠对于降低“Z”形凹口处Von-Mises应力有一定好处,降低的幅度较大,该处应力的降低减小了因蠕变而出现裂纹的可能性,提高了叶冠的寿命,保证了发动机工作的安全性。
3 锯齿冠优化前、后减振特性对比
锯齿冠经优化后,不仅应力水平发生改变,而且由于叶冠本身的形状发生变化,叶盘结构的振动特性也将发生变化。通过模态分析和谐响应分析对锯齿冠优化前、后的减振特性进行对比。
3.1 锯齿冠优化前、后模态分析对比
以单自由度系统有阻尼固有频率计算公式[21]为例

式中:棕d、棕n分别为考虑和不考虑干摩擦阻尼时的固有频率;孜为缘板阻尼器的阻尼比,一般为0.01~0.1[22]。则棕d与 棕n的关系为

由此分析可知,叶冠提供的阻尼对叶盘结构固有频率的影响很小,故设置叶盘结构的约束、接触类型与静载荷计算时相同,施加离心载荷,进行有预应力的模态分析,计算得到叶冠优化前、后第1、2阶动频与倍转速线的关系如图11所示。从图中可见,第1阶动频与3倍转速线较为接近,优化前、后变化较小;第2阶动频与5倍转速线较为接近,叶冠优化后,叶盘结构的第2阶动频较原结构远离了5倍转速线,较原结构升高3.7%。
计算不同转速下叶盘结构的动频,得到叶冠优化前(实线)、后(虚线)的坎贝尔图如图12所示。从图中可见,由于上游静子叶片数为55片,转子每转1周受到55次尾迹气流激振力,所以激励线的谐波数k=55,其斜率为55/60。在坎贝尔图中激励线与各阶动频交点为潜在的共振频率点,叶冠优化后叶盘结构的坎贝尔图整体上移,叶冠优化前、后激励线与第5阶动频交点对应的转速与慢车状态下转速裕度较小,优化前、后分别为6.7%、4.8%。

图11 锯齿冠优化前、后动频与倍转速线关系

图12 锯齿冠优化前、后叶盘结构坎贝尔图
3.2 锯齿冠优化前、后谐响应分析对比
根据模态分析结果利用模态叠加法对叶盘结构进行谐响应分析,在叶尖前缘一点施加幅值为10000 N的正弦周期性气流激振力。王春健等[23]在进行涡轮叶片谐响应分析时实测系统阻尼比为0.077,由于阻尼比与系统固有频率成反比[21],本文叶盘结构固有频率较文献[23]中的大,故阻尼比应小于文献[23]中的值,取为0.05,求解不同激振频率下系统的振动响应,从而获得系统的幅频响应曲线如图13所示。
从图中可见,叶冠优化后系统的幅频特性曲线较优化前“滞后”,第1阶固有频率附近振动响应最大,叶冠优化后振动响应有所减小,但不明显;第1、2阶固有频率之间存在振动响应峰值,叶冠优化后振动响应同样有所减小;激励频率大于2 kHz之后,优化前、后系统的幅频特性曲线基本重合。

图13 锯齿冠优化前、后系统幅频特性
4 结论
(1)针对典型锯齿形叶冠,提出了切除部分叶冠结构的轮廓优化方法和优化原则,且优化原则对一般锯齿冠普遍适用。
(2)切除叶冠的叶型对降低叶身与叶冠、叶身与下缘板以及“Z”形凹口连接处的应力效果明显,典型叶片在这3个部位的Von-Mises应力分别降低16.1%、5.6%、24.5%。
(3)典型锯齿冠优化后对轮盘辐板应力影响较小,在辐板处最大径向应力降低0.4%,在盘心处最大周向应力降低0.7%。
(4)叶冠优化后叶盘结构各阶动频较原结构的有所增大,叶盘结构第1阶动频优化前、后变化较小,第2阶动频优化后较优化前远离了5倍转速线。叶冠优化前、后激励线与第5阶动频交点对应的转速与慢车状态下转速裕度均较小,分别为6.7%、4.8%,优化前、后均不应在此转速下长时间停留。
(5)叶冠优化后系统的幅频特性曲线较优化前“滞后”;第1阶固有频率附近振动响应最大,叶冠优化后振动响应有所减小,但不明显;激励频率大于2 kHz之后,优化前后系统的幅频特性曲线基本重合,即叶冠优化后不影响减振作用。
优化后的锯齿冠对涡轮转子气动性能和冷却效率的影响本文没有涉及,需进一步计算与验证。

