基于改进NS-SOMA的变循环发动机解耦控制方法
何凤林,李秋红,陈尚晰
(南京航空航天大学江苏省航空动力系统重点实验室,南京210016)
0 引言
几何可调的变循环发动机(VCE)能够在超声速状态下提供足够的单位推力,在亚声速状态下降低耗油率,是应用于第4代多用途战斗机的理想动力装置[1-2]。国外早在20世纪70年代就开展了变循环多变量控制技术研究[3-4]。Shutler[5]研究了变循环发动机的控制结构设计方法,通过灵敏度分析,以燃油流量、喷口面积控制风扇转速和外涵出口马赫数;Frederick[6]则基于鲁棒多变量控制方法对H∞技术进行改进;文献[7]研究了3输入3输出2个分块的XTE76变循环发动机控制结构,其中双变量分块以燃油流量和尾喷口面积控制风扇换算转速和发动机压比,单变量分块以外涵出口面积控制外涵出口和内涵出口的总压比,2个分块的控制器相互独立。在国内,李嘉[8]针对飞行包线内外部扰动引起的多变量鲁棒自适应控制器设计问题提出了基于射影算子的自适应律设计方法,同时针对建模不确定性提出基于LQR基准控制器的增广模型参考自适应跟踪补偿方法[9];王元[10]利用不同的优化算法对VCE的控制规律进行优化设计;聂友伟[11]针对变循环性能寻优控制提出了序列二次约束二次规划(SQCQP)算法,其控制模块输入输出与王元的控制系统设计相同,但观察其仿真可以看出控制效果不佳,上升时间较长并且有超调。
变循环发动机具有更多的可调几何机构,应采取3变量的闭环控制结构。由于多变量控制系统控制器参数较多,设计过程中可以调整参数使得控制系统获得满意的性能,而群智能算法由于其全局搜索能力,在控制器参数优化过程中得到了广泛的应用[12-13]。其中自组织迁移算法具有需要设置的参数少、收敛速度快的特点,为此本文提出了1种改进非支配序自组织迁移算法(Non-dominated Sorting Self-organizing Migration Algorithm,NS-SOMA),实现对控制器参数的多目标优化。本文针对文献[7]XTE76变循环发动机的分块控制结构开展研究,鉴于其2个单独分块之间的耦合,提出了分块之间的解耦控制方法,同时研究了3输入3输出不分块的控制器设计方法,提出了基于改进NS-SOMA进行多目标优化的解耦控制方法,并在变循环发动机部件级模型[2]上验证3种控制结构的仿真效果。
1 2分块独立控制结构
以某型带核心机驱动风扇级(CDFS)的双涵道变循环航空发动机作为研究对象,其结构如图1所示。

图1 发动机结构
从图中可见,相较于普通航空发动机,变循环发动机增加了模式选择活门、核心级风扇(CDFS)、前可调面积涵道引射器(FVABI)以及后可调面积涵道引射器(RVABI)。
文献[7]中的XTE76发动机的主控制系统结构如图2所示(总体控制结构见文献[7])。为了简化控制器设计,整个控制系统采用双变量分块和单变量分块的二一分块控制方式,控制器之间相互独立。

图2 XTE76发动机的主控制器结构
双变量分块控制输入为燃油量Wfb和尾喷管面积A8,被控制输出为低压转子转速nf和发动机压比仔epr;单变量分块控制输入为后可调涵道引射器面积Arvabi,输出为外涵出口与内涵出口总压之比仔lepr。
由于2个分块之间相互独立,可以按照传统的双变量控制方法和单变量控制方法分别设计控制器,对发动机进行控制。然而由于变循环发动机是1个复杂的被控对象,变量之间存在着不可忽略的耦合,2个分块之间必然相互影响,为此本文开展2个分块之间解耦的控制方法研究。
2 分块之间解耦的控制方法
实际发动机在工作时,Wfb和A8的变化会引起仔lepr的变化,同样Arvabi的变化也会引起nf和仔epr的变化。在设计点采用小扰动法进行输出对输入变化的灵敏度分析,对各输入分别施加1%的小阶跃,记录输出相对输入的变化量,得到。可见虽然喷口变化引起仔lepr的变化较小,但其他变量引起另外分块输出均在20%以上,为此需要对分块控制器进行解耦研究。
首先进行双变量分块的控制器设计,将Arvabi视为干扰量,抑制其对nf和仔epr的影响。考虑各执行机构动态,得到按输出分块之后的被控对象模型

式中:x1=[WfbA8Arvabinfnc]T,为双变量分块的状态变量;x觶1为状态变量的 1 阶导数;u1r=[WfbrA8r]T,为燃油量和尾喷口面积指令;u2r=Arvabi,r为RVABI指令;y1=[nf仔epr]T,为双变量分块的输出;y2=仔lepr,为单变量分块的输出。
应用现代控制理论,采用状态反馈控制方法,并考虑鲁棒跟踪性能和干扰抑制能力,在控制系统的前向通路中引入输入信号的内模。由于输入信号在稳态的值恒定,因此可以将其理想化为阶跃信号,则其内模表现为串联在前向通路中的1个积分环节,得到闭环系统控制结构如图3所示[12]。

图3 双变量分块控制器结构
从图中可见,状态反馈控制率为
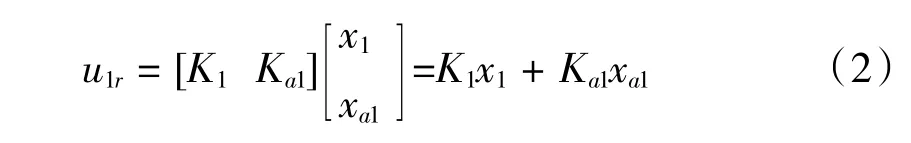
式中:K1为x1的状态反馈矩阵;Ka1为xa1的状态反馈矩阵;xa1为误差的积分。
则其状态反馈控制律的设计模型为

将式(2)带入式(3)得到闭环系统模型为
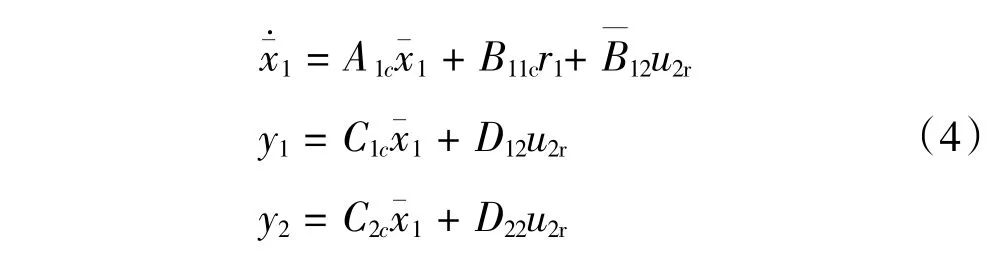
常用的状态反馈控制方法包括极点配置方法和线性二次型调节器(LQR)方法[14],对于多变量系统,给定1组期望的闭环极点,其状态反馈控制器不惟一,且零点对系统性能也会产生较大的影响,为此本文以LQR控制方法求解状态反馈控制器,控制目标为输出y1能够快速输入信号r1的变化,并且超调量小,同时能够有效抑制u2r对y1的影响,因此定义控制系统的性能指标为

式中:籽1为超调惩罚系数;滓1为超调量;Ty1u2r(s)为从u2r到y1的闭环传递函数。
性能指标J1反映了对输出跟踪和无超调的性能要求,性能指标J2通过无穷范数反映了对干扰抑制的性能要求。能够快速响应的系统通常带宽较大,对干扰抑制不利,因此J1和J2为1对互相矛盾的性能,在控制器设计过程中,需要均衡考虑二者对系统性能的影响,适合采用多目标优化方法对问题进行求解。由于本文采用LQR方法计算状态反馈控制器参数,为此待优化参数为LQR控制器的加权矩阵Q、R,其为状态量和控制量的加权,对于本文所研究的系统,所形成的二次型指标为

则 Q∈R7×7,R∈R2×2。
将Q、R矩阵视为对角阵,则共有9个待优化参数,采用改进的NS-SOMA多目标优化算法对参数进行优化。区别于单目标优化算法,多目标优化算法在选择算子之前根据个体之间的支配与非支配关系进行排序,其非支配解集形成Pareto前沿面。在Pareto前沿面上的解均具有较好的性能,而本节主要针对分块解耦研究,所以选择Pareto前沿面上干扰抑制能力最优的个体形成Q、R矩阵,进行控制器设计,得到如式(2)所示的状态反馈控制律,进而形成如式(4)所示的闭环控制系统。
在完成双变量分块设计的基础上,进一步开展单变量分块控制器设计,其基于内模原理的控制系统结构如图4所示。从图中可见,此时的单变量分块为以u2r为输入、y2为输出、r1为干扰的被控对象,与式(4)的相同。

图4 单变量分块控制器结构
状态反馈控制率为

则可以采用与双变量分块相同的控制方法进行控制器参数的优化设计。采用解耦方法之后的控制系统结构如图5所示。

图5 分块解耦控制系统结构
3 3变量不分块控制方法
分块解耦控制是将2个分块之间的耦合关系作为外部干扰处理,而文献[7]中的设计方法没有考虑2个分块之间的耦合,在耦合较小的情况下可以采用这种控制结构;若耦合较大,采用不分块的综合设计更易获得良好的性能。为此本文还研究了3输入、3输出的综合控制方式,即将式(1)中的输入输出合并考虑,由于变循环发动机控制过程中通常保持仔lepr为常数[6-7],为此在3变量综合控制中,优化的目标为

式中:滓2为最大耦合响应幅值;籽2为惩罚系数。
若想使y1能够快速无超调跟踪r1,势必会引起y2较大的耦合响应,为此二者同样为1对矛盾的指标,同样适合采用多目标优化的方法进行控制器设计。本文采用与双变量分块相同的设计方法进行控制器设计,只是将评价指标改成了式(8),以改进的NS-SOMA进行控制器参数优化,实现基于多目标优化的控制回路之间的解耦。
4 基于NS-SOMA的控制器参数优化
自组织迁移算法是1999年提出的1种模拟社会环境下群体自组织行为的新型群体智能算法[15],具有需要设置的参数少、收敛速度快的特点。由于多变量控制器对应矩阵元素较多且元素取值差异较大,NSGAⅡ优化时速度较慢,影响了收敛的速度和精度,为此本文采用自组织迁移算法代替传统的遗传算法。SOMA通过改变粒子的位置实现对最优解的逼近。种群中的最优个体称之为种群领导者[16]。在每次迭代过程中,除了领导者以外的所有个体均向领导者的方向迁移,每次迭代之后更新种群领导者。SOMA算法的变异与其他进化算法不同,通过参数PRT获得摄动。这个参数的意义跟遗传算法中的变异一样。
SOMA算法以种群领导者为方向,对其他个体进行迁移,迁移过程如下:
(1)根据个体维数,随机生成介于0~1之间的值,若该数值小于参数PPRT,摄动向量Pv对应元素为1,否则为零。
(2)生成迁移后的个体

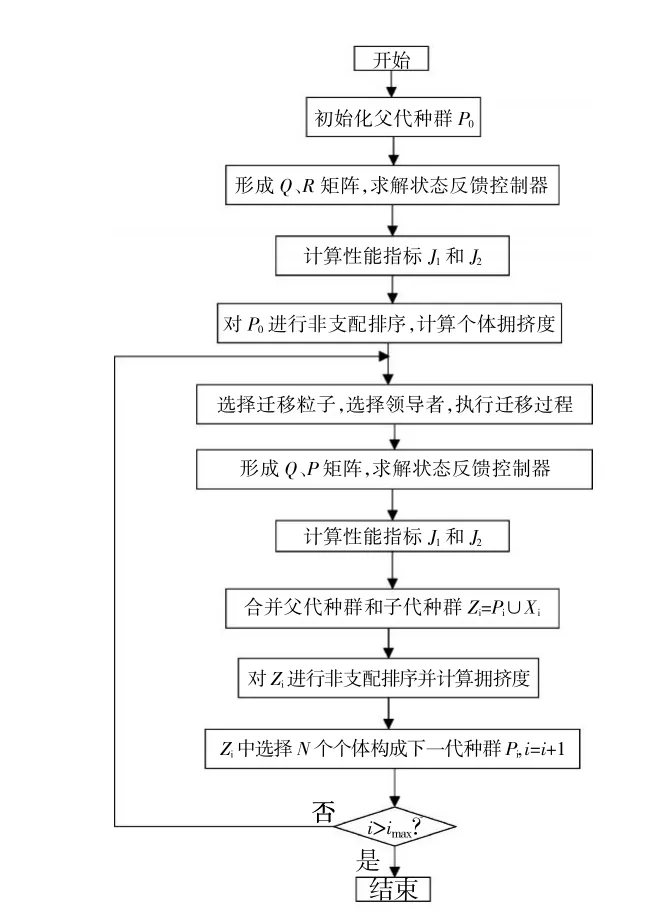
(3)贪婪选择。计算适应度值f(xtemp);若f(xtemp) (4)增加迁移步长 Sstep=Sstep+Sstep,若 Sstep>Pp,则当前粒子迁移结束,否则转(1)。 由此可见,基本SOMA算法解决的是单目标优化问题,因此具有领导者,也就是全局最优粒子,而对于多目标优化来说,没有最优个体,为此需要对其进行改进。本文对每个即将迁移的粒子进行非支配排序,从支配序为1的个体中随机选择1个个体为领导者,则不同的粒子具有更大的机会向不同领导者迁移,可以确保种群的多样性,同时确保领导者本身的优越性。为了提高算法的收敛速度,记支配序为1的个体形成前沿面中间位置的个体为x1,mid,以个体与其的欧氏距离为评价标准dist=||xi-x1,mid||2,从中均匀选出部分粒子进行迁移,避免了迁移所有粒子影响收敛速度,同时可以设置较大的初始种群规模,以获得解的多样性。 为验证改进后的NS-SOMA的有效性,采用3个典型多目标优化算法对函数ZDT1、ZDT2、ZDT3进行测试[17],设定初始种群数为100,根据距离,每隔10个粒子选择1个进行迁移,则每代有10个粒子参加迁移,迁移步长Sstep=0.11,最大迁移路径Pp=3,摄动参数PPRT=0.9。当允许适应度函数调用次数为10万次时,3个测试函数获得的Pareto前沿均收敛于已知Pareto最优解P*上,ZDT3的对比如图6所示。以GD指标评价其收敛精度(GD指标为Pareto解集与已知Pareto最优解的距离),允许的适应度函数调用次数分别设为10万次、3万次和1万次,每种情况运行10次优化程序计算平均GD指标,其结果与文献[18]中的结果(支配的自组织迁移算法(EMSOMA)及经典NSGAII算法结果的对比见表1。 图6 ZDT3的Pareto前沿效果 表1 NS-SOMA的GD指标对比 从表中可见,所提出的改进NS-SOMA算法在测试函数ZDT1和ZDT2上获得的GD值更小,解集更接近Pareto最优解。在ZDT3上的GD值大于采用EMSOMA算法得到的,但也远小于采用NSGAII算法得到的,同时发现在ZDT3上,调用评价函数1万次的GD值反而小于3万次和10万次的,进一步研究发现,此时解比较密集,其拥挤度指标比较差。改进的NS-SOMA算法仅需要较少的评价函数调用次数就能取得优秀的解,验证了其在收敛精度和速度上的优越性。实际上,SOMA算法与同样通过改变粒子位置来实现进化的粒子群算法相比,其在多目标优化上的效果也具有明显优势[19],但其获得的关注度远低于粒子群算法。 以此多目标优化算法优化分块解耦控制器参数和不分块的综合控制器参数,优化流程如图7所示。参数设置与测试时相同,以其干扰抑制效果最佳的Q、R值设计状态反馈控制器。 首先基于控制器设计所用的状态变量模型对解耦控制器与不分块综合控制器的动态跟踪性能和解耦性能进行对比验证。状态变量模型采用经典的拟合法建立[20],具有较高的精度。在模型中,nf、仔epr阶跃1%,仔lepr不阶跃,线性模型输出响应曲线如图8所示。从图中可见,不分块系统获得了更快的响应速度,其上升时间和调节时间明显小于分块解耦控制系统的,其仔lepr耦合最大幅值虽然大于分块解耦控制系统的,但其波动幅度却明显小于分块解耦控制系统的。 图7 改进NS-SOMA算法流程 图8 线性模型输出响应 为了进一步对比控制器效果,将通过优化获得的分块解耦控制器、不分块综合控制器与文献[7]中分块控制器(分块控制器仅以最优跟踪进行单目标优化)进行控制效果对比,在变循环发动机部件级数学模型[2]上开展仿真验证,该模型能够完整模拟变循环发动机模式切换过程,并且在飞行包线内、不同工作模式下的性能符合变循环发动机基本性能规律。在高度 H=0 km、马赫数Ma=0、nf=100%的状态下,t=2 s时,保持仔lepr不变,nf、仔epr同时阶跃 1%,各输出响应如图9所示。 从图中可见,在3种控制结构下,nf、仔epr均实现了对阶跃1%目标的快速跟踪,不分块控制系统在综合响应速度上占优势。观测2个变量阶跃引起的仔lepr耦合,可见分块系统的耦合最大幅值约为0.25%,分块解耦之后耦合降低到0.2%,不分块解耦之后耦合降低到0.175%,与分块控制系统相比,最大耦合降低30%,且随着最大耦合幅值的减小,耦合的作用时间也减短,从而说明采用多变量综合控制的方式能够有效抑制回路之间的耦合,同时也说明本文所提出的多目标优化解耦控制方法的有效性。 图9 部件级模型输出响应 本文针对变循环发动机的多变量控制结构,在国外采取的3变量2个分块控制的基础上,研究了2个分块之间的解耦控制方法和3变量综合控制的解耦方法,提出了基于改进NS-SOMA的多目标优化解耦控制方法,根据欧式距离选择迁移粒子,提高了算法的收敛速度和寻优精度。针对3种控制结构在变循环发动机上开展了仿真验证,结果表明分块解耦控制方法能够降低回路之间的耦合,不分块综合解耦控制方法更能够发挥多变量控制系统的性能效益,取得了更好的解耦控制效果。

5 仿真对比验证



6 结束语

