ANSYS软件在材料力学弯曲正应力教学中的运用

陈远远

摘要：作为应用型本科院校土木工程专业的专业基础课.材料力学对后续课程的学习影响较大。由于材料力学弯曲正应力公式推导过程复杂，教师与学生在教与学的过程中都面临较大困难。研究变化悬臂梁的截面形式，研究纯弯曲及横力弯曲情况下悬臂梁正应力分布情况，将ANSYS软件引入弯曲正应力教学中，提高了分析结果的可视性。

关键词：ANSYS软件;材料力学;弯曲正应力教学

材料力学是应用型本科院校土木工程专业的专业基础课。弯曲变形是材料力学研究的四大变形中的一种，这类变形往往出现在梁构件中。在外力作用下梁截面内力为弯矩和剪力，弯矩产生的正应力是影响强度和刚度的主要因素，故应对弯曲正应力进行严格的推导。材料力学教材是从变形几何、物理及静力学三大关系人手推导梁横截面的正应力公式的.涉及较多的数学公式，推导过程逻辑性强，且三大关系多以微积分方程式体现，学生在学习这部分知识时，往往死记教材上的内容，学习效果不佳。而且，在进行纯弯曲梁的正应力测试实验过程中，学生肉眼无法观察到梁在弹性范围内的变形情况，不能较好地理解变形的过程，感性认识不足进一步导致学生对弯曲正应力这部分知识点的理性认识缺乏兴趣。

一、ANSYS软件在弯曲正应力教学中的优势

ANSYS应用软件的出现，很好地解决了材料力学课时少教学难度大这一问题。目前，ANSYS软件在弯曲正应力教学中的优势，主要表现在以下两个方面。

（一）提升教学效果

ANSYS软件能较好地模拟材料力学中的梁，可显示各种截面形状梁的应力分布情况。学生通过观察ANSYS软件以动画形式展示出的梁截面应力分布情况，可加深对弯曲正应力相关知识点及公式的理解与掌握，提高对弯曲正应力的学习兴趣与学习热情，从而降低该部分的学习难度。

（二）培养学生的实际应用能力

ANSYS软件如能在弯曲正应力教学中被有效应用，可发挥其强大的快捷建模能力、网格处理能力以及图形显示能力。通过ANSYS软件对纯弯曲梁的变形现象和横截面上正应力分布规律进行验证，可以促进学生对基础知识点的掌握，加深学生对实际梁构件工程背景的理解，拓展学生的视野，培养学生理论联系实际的能力。

二、ANSYS软件在弯曲正应力教学中的应用

梁在只有弯矩没有剪力，且任一横截面上的弯矩都相同的情况下的弯曲称为纯弯曲，根据纯弯曲梁横截面正应力的公式σ=My/Iz可以推导出，横截面上任意一点的弯曲正应力，与它到中性层的距离y成正比，与截面对中性轴的惯性矩IZ成反比。梁在既有弯矩又有剪力的情况下的弯曲称为横力弯曲，横力弯曲时梁的正应力计算利用了纯弯曲的结论，但横力弯曲梁上不同横截面的弯矩不同，任意一点的弯曲正应力，除了要考虑点到中性层的距离和截面对中性轴的惯性矩的影响，还要考虑点所在截面的弯矩的影响。

对于纯弯曲梁和横力弯曲梁，若中性轴是横截面的对称轴，则梁横截面正应力数值关于中性轴对称，应力符号则关于中性轴相反。为了让学生直观形象地了解纯弯曲及横力弯曲正应力的分布规律，更好地理解弯曲正应力的计算，也为了提高学生的形象思维能力，使其更好地理解教材内容，笔者主要研究了等截面及变截面两种截面形式的悬臂梁在纯弯曲及横力弯曲情况下的应力分布情况，分析ANSYS软件在弯曲正应力教学中的应用。

（一）等截面悬臂梁横截面上的正应力

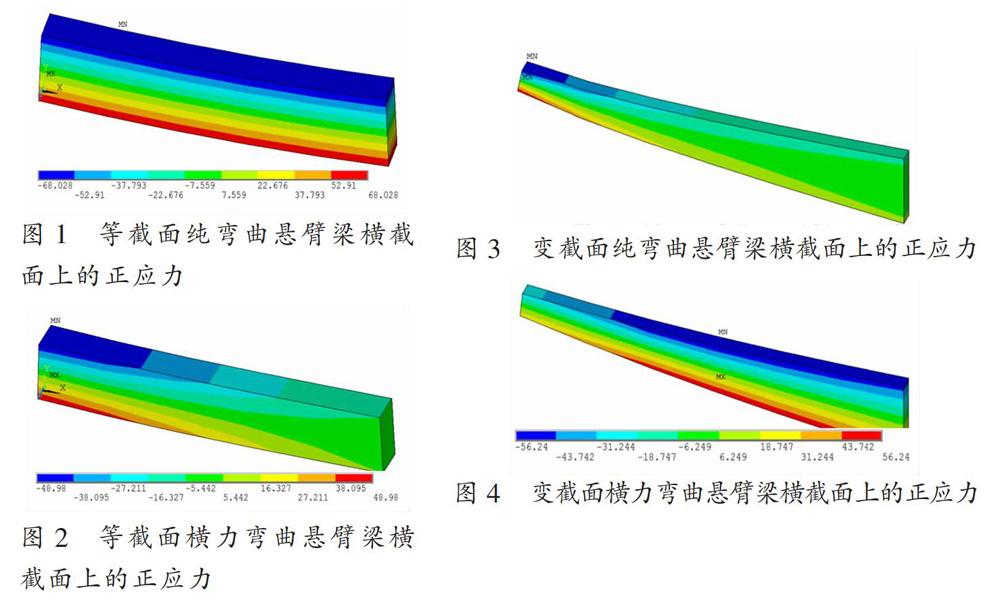
利用ANSYS软件建立等截面纯弯曲悬臂梁及等截面纯弯曲悬臂梁模型，模型左端为固定端，在自由端施加外荷载。经过后处理得到图l、图2所示的弯曲正应力分布图。图1显示纯弯曲悬臂梁正应力分布色度沿着梁的高度呈现出分层变化的规律，且分布色度图显示出该梁以中性层为界，距离中性层越远处应力值越大，中性层以上纤维受压，中性层以下纤维受拉，且任意一个横截面上的正应力数值都关于中性轴对称，这些现象都与理论公式计算出的结果一致。由图1可知纯弯曲梁内部距中性层与同样高度的纤维层所受的正应力值相同，正应力最大值出现在整个梁构件的每个截面的外边缘上。根据材料力学内力分析等截面纯弯曲梁每一个横截面上所受弯矩相同，且Iz也相同，由σ=My/Iz可得，任意两点只要y一致，σ便相同，即距中性层同样高度的纤维层所受正应力值都相同，因此分布色度沿着梁的高度呈现出分层变化的规律。由于该梁每个截面所受弯矩都为整个梁构件的弯矩最大值Mmax，在截面不改变的情况下，抗弯截面模量Wz不改变，由理论公式σmax=Mmax/IZ可知，正应力最大值出现在整个梁构件的每个截面的外边缘上。

而图2显示横力弯曲悬臂梁中性层以上纤维受压，中性层以下纤维受拉，任意一个横截面上的正应力数值也关于中性轴对称，这与图1观察到的现象一致。但图2显示出横力弯曲悬臂梁正应力分布色度沿着梁的高度变化不具规律性，距中性层同样高度的纤维层所受的正应力值不同，距中性层不同高度的纤维层所受的正应力值反而相同，根据材料力学内力分析等截面横力弯曲梁每一个横截面上所受弯矩都不同，但TX相同，由σ=My/Iz可得，任意两点只要y一致，σ便不相同，距中性层同样高度的纤维层所受正应力值都不相同，因此正应力分布色度沿着梁的高度未呈现出分层变化的规律。而如果任意两点y不一致時，只要My/Iz相同，σ便相同，距中性层不同高度的纤维层所受的正应力值反而相同。由图2可知横力弯曲梁正应力最大值出现在固定端截面的外边缘上，根据材料力学内力分析横力弯曲梁横截面上的弯矩沿着梁轴变化，且最大值出现在固定端截面上，在等截面情况下，抗弯截面模量Wz不改变，由理论公式计算可知正应力最大值也出现在固定端截面的外边缘上。

（二）变截面悬臂梁横截面上的正应力

利用ANSYS软件建立变截面纯弯曲悬臂梁及变截面横力弯曲悬臂梁模型，模型右端为固定端，在自由端施加外荷载，求解得到图3、图4所示的弯曲正应力分布图。

从图3、图4可以看出，在变截面的情况下，横力弯曲悬臂梁相比纯弯曲悬臂梁，正应力分布色度沿着梁的高度更具分层变化的规律性，根据材料力学内力分析可知，变截面横力弯曲悬臂梁每一个横截面上所受弯矩M及IZ的变化规律都是离固定端越远则越小，根据公式σ=My/Iz可得，不同横截面上的点的y值在差异不大的情况下，σ便会相同，而变截面纯弯曲悬臂梁每一个横截面上所受弯矩都相同，但离固定端越远的横截面值IZ越小，根据公式σ=My/Iz可得，不同横截面上的点的y值在差异较大的情况下，σ才会相同，因此图4相比图3，正应力分布色度沿着梁的高度更具分层变化的规律性。

三、结论

在弯曲正应力教学中，教师采用AN.SYS软件对比分析不同截面形式的悬臂梁在纯弯曲及横力弯曲状态下的弯曲应力，提高了分析结果的可视性。通过色度图，学生可直观地看出同种截面形式的梁在不同弯曲形式下的截面正应力分布规律，及不同截面形式的梁在同种弯曲形式下的截面正应力分布规律，有利于学生主动思考并总结截面形式及弯曲形式对梁截面正应力的影响，进而增强学生解决关于弯曲变形问题的能力，提高学生学习兴趣及效率。将理论计算和ANSYS分析结果进行对比，实验证明，降低了理论公式学习的难度，也证明了理论公式的正确性及实用性。