二进制翻译正确性及优化方法的形式化模型
傅立国 庞建民 王 军 张家豪 岳 峰
(数学工程与先进计算国家重点实验室(战略支援部队信息工程大学) 郑州 450002)
传统意义上的二进制翻译是指将源平台指令集的指令序列翻译成其他平台指令集的指令序列的过程.随着虚拟化技术应用的兴起,二进制翻译技术作为跨指令集架构虚拟化实现的核心技术被广泛关注[1].二进制翻译中的动态翻译方式既能够在程序运行期间动态地解释代码片段,也能够结合程序运行的时空局部性特征实现性能调优,亦可以再现程序在源平台复杂的运行时行为,从而成为体系结构设计、程序性能优化、安全性分析以及软件移植的研究热点.
为实现二进制程序到其他平台的有效移植,需要确保二进制翻译过程的正确性和有效性.正确性要求源平台二进制程序的逻辑功能在宿主平台上被予以等价的实现;有效性关注的是源平台代码在宿主平台上运行时的效率.因此,二进制翻译技术在应用研究中的问题总是可以归结为翻译的正确性问题和翻译的效率问题.
现有相关问题的研究大多是对限定翻译系统工程实现的探讨,局限于具体翻译系统缺陷的修复.以选定的翻译器或者翻译框架为条件,不利于深入研究二进制翻译的正确性和运行效率.如用于精确处理中断、精确处理异常还原的二进制翻译器,则更关注其翻译的正确性;而用于软件无源移植的翻译器则更关注其运行效率[2-3].
在设计二进制翻译器时,将翻译过程的正确性和效率作为整体进行研究,能够预见和避免类似限定框架下存在的种种问题.例如,在新型体系架构研发的研究中,为了解决传统的通过功能模拟的方法收集典型行为特征速度很慢的问题,使用了动态二进制翻译技术来加快程序行为分析.然而该方法却也引入了分析误差,可见追求翻译的有效性时翻译的正确性会受到影响[4].因此,翻译正确性和翻译效率以及两者之间关联性的研究对于二进制翻译系统框架的设计具有重要意义,特别是在对一些优化方法的正确性进行理论验证的过程中.
在现有的二进制翻译正确性验证相关的研究中,采用自动化形式化的验证方法已经比较普遍.如文献[5]于2011年提出了对动态翻译过程中SIMD指令的翻译进行运行时验证的方法;文献[6]于2015年提出同时支持动态翻译和静态翻译的验证方法,却局限于仅对部分制定翻译结果的验证;文献[7]于同年提出了使用形式化的方法讨论操作数和操作数约束的优化过程,然而该模型对于二进制优化方法的描述不具备通用性.因此为了能够对翻译的正确性和优化方法的有效性进行一致性的研究,本文对翻译过程及其优化方法构建适当的形式化模型.
1 基于指令解释的映射模型
文献[8]借鉴文献[9]中可计算代数系统中同构的性质,构建了机器模拟过程和动态二进制翻译过程的形式化模型.该模型将机器模拟的过程定义为由源机器状态和指令解释函数组成的有序对到由宿主机器状态和指令解释函数组成的有序对的映射;继而在此基础上,将动态二进制翻译过程归约为机器模拟过程的动态优化方法,从而描述了动态二进制翻译过程相较于机器模拟过程所优化的对象和方法.
1.1 机器模拟的形式化描述
定义1.机器描述1.机器为M=(S,I,γ).其中,S表示机器的状态集;I表示机器的指令集;γ:I×S→S表示机器指令在指定机器状态下的解释函数.
当指令i∈I作用于状态s∈S,其后继状态s′可表示为s′=γ(i,s).
定义2.解释函数.指令路径i*=i0,i1,…,im-1∈I*的解释函数为γ*:I*×S→S,表示进行m次γ的迭代操作,即γ(im-1,…,γ(i2,γ(i1,γ(i0,s0)))…)=γ*(i*,s0).
1.2 机器模拟的性质
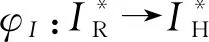

Fig. 1 The mapping relation in machine simulation图1 机器模拟中的映射关系
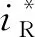
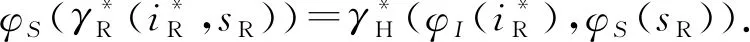
(1)
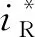
文献[8]将动态二进制翻译归为机器模拟过程的动态优化技术,指出其实质是源机器平台上执行路径在宿主机器上的再次编译,并参照式(1)给出了动态二进制翻译的一般性质.
1.3 现有模型存在的不足
基于指令解释的映射模型通过式(1)描述了机器模拟过程和动态二进制翻译过程的一般性质.文献[10]在协同设计虚拟机的模拟研究中使用文献[8]中的模型对模拟过程中的一些性质给予了形式化的论证,文献[5-7]在使用这种描述方法的同时也暴露了该模型存在的一些不足.
1.3.1 确定的指令路径
在该模型中,宿主机器对源机器的模拟和翻译默认源机器执行前的初始状态以及之后执行的指令序列是确定的.而在实际翻译过程中,仅加载待翻译可执行文件后的初始状态以及机器指令执行行为的相关解释是已知的.在无法确定具体指令执行路径时,便无法通过映射得到宿主机的指令执行路径.
1.3.2 指令路径的映射
假设源机器执行的指令路径是确定的.通过映射得到宿主机器的指令路径,执行该指令路径使得宿主机器从初始状态得到满足条件的结束状态.然而对于模拟和翻译过程,具体执行的指令路径只是一个实现.以指令和固定的指令序列作为映射元素的翻译方式,破坏了指令序列更高层次等价翻译的可能性,这对于构建更高形式优化方法的描述是不利的.
1.3.3 指令路径的执行效率
该模型主要用于描述模拟和翻译过程的正确性.仅使用状态映射函数及其优化函数描述本地指令路径的执行效率,不足以深入讨论翻译方法的优化问题.将翻译过程表示为指令路径间的映射过于抽象,无法刻画动态翻译过程的开销.该模型的翻译过程与源机器具体的指令路径相关,优化也是基于具体指令路径的.不同的指令或者指令路径其指令解释函数可能是相同的,然而这些等价的指令(序列)若按照指令为单位的翻译方式,其在宿主机器翻译得到的指令(序列)之间执行开销的差距可能极其大.翻译过程的优化也包括求解更为有效的本地实现.然而在指令映射的方法不足以描述生成的本地指令路径的效率.
综上所述,在分析翻译效率时,该模型中的状态映射函数及其优化函数并不能涵盖翻译过程中所有重要的因素.能够对翻译过程正确性和优化方法有效性进行分析的形式化模型,需要对影响翻译正确性和翻译效率的所有因素的概念加以定义,然后结合这些因素对二进制翻译的正确性和翻译中优化方法的定义和性质进行讨论.
2 二进制翻译过程的抽象及其形式化
二进制翻译过程需要源机器架构特征描述和二进制可执行文件一同作为输入.由于宿主机器只能执行本地指令序列,待翻译的程序在宿主机器可以有2种存在形式:1)完整的宿主平台可执行文件;2)需要其他程序配合的零散的指令序列片段.然而不论是以哪种形式,本地存储的指令序列在执行时都是宿主机器对二进制程序在源机器上执行过程的模仿.
系统性地讨论翻译过程的正确性和翻译过程的优化,需要对二进制翻译过程进行抽象.对二进制翻译过程的抽象即对源机器程序的执行过程以及对该过程模仿过程的抽象,且两者在本质上都是机器的指令执行过程.所以抽象机器上指令执行的过程是刻画二进制翻译过程的基础.
2.1 机器的抽象描述
基于指令解释的映射模型本质上是利用指令的操作语义描述指令执行过程中机器状态的变化过程,以算数表达式的形式用指令解释函数定义了指令执行的过程.机器M=(S,I,γ)从状态s∈S执行指令i到达状态s′∈S的过程,指令解释函数的操作语义可描述为
i,s→s′.
(2)
然而,基于这种描述的指令解释函数在描述指令序列的解释函数时,在对每条指令的解释函数进行复合操作的时候需要明确每条指令的解释函数,这需要满足以下2点:一是指令序列是已知的;二是每条指令的解释函数是可表示的.为了弱化指令路径对指令迭代执行过程描述的限制,需要对指令执行过程进一步抽象.
文献[11]将动态二进制翻译过程概括为查找、翻译和执行3个过程的迭代.该描述与处理器从存储器取指、译指(取值)和执行(返值)的执行过程相符.因此,指令执行的路径是和机器状态密切相关的,每个机器状态的后继状态是通过执行从该状态中获得的指令而得到的.因此机器指令的执行过程可以描述为γ(i,s)=γ(f(s),s)=s′.其中f表示从执行前的状态s获取指令i的过程.在状态解释函数γ中,2个参数都是状态s的函数,可将其缩略为
γ(s)=s′.
(3)
如此,函数γ定义了一个机器状态间的映射关系,描述了机器状态在指令执行中的状态迁移过程.这种描述是对机器执行指令的行为加以抽象,而并非对具体指令的执行效果进行描述.此时γ不再是机器指令解释函数,而是机器指令执行的指称函数.
使用状态转移函数可以表示任意指令和指令序列的执行.根据指称语义及其操作语义的一致性[12],结合式(2)可将指令i∈I的状态转移函数表述成
γ(i)={(s,s′)|i,s→s′}.
(4)
式(4)中使用函数γ描述了指令i的指称语义,称为指令i的指称.当讨论范围扩大为整个指令集I时,可以将指令集I的指称语义以函数的形式表述为
γ=γ(I)=∪i∈I{(s,s′)|i,s→s′}.
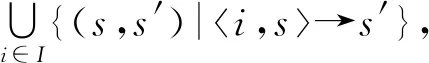
综合以上分析,对机器定义如下:
定义3.机器描述2.机器为M=(S,γ).其中,S表示机器的状态集;γ:S→S表示机器指令集的指称函数.
指称函数γ定义了状态集S上的一个二元关系,表示指令执行前后状态的变换关系,故也可以将其称作状态迁移函数.
2.2 程序执行的抽象
重新定义机器描述后,程序执行的过程也可以得到进一步的抽象.设加载完可执行文件后的机器状态为s0∈S,程序执行的过程可以用机器指令的迭代执行过程表示,而程序执行过程状态和程序执行结果的求解问题则被归约为状态s0后继状态的求解过程.
状态s0及其后续状态可以表述为有序集合{γ0(s0),γ1(s0),γ2(s0),…,γn(s0),…}.s0∈S,n∈N,其中γ0(s0)=s0.为了深入刻画程序执行的性质,需要对该集合中元素间的关系进一步讨论.
定义4.状态间的二元关系.在机器状态集合上存在二元关系≤,对于状态a和状态b,如果b∈γ*(a),记作a≤b.
性质1.当集合γ*(s0)中不存在2个相等的元素时,集合γ*(s0)上的二元关系≤为全序关系.
证明.
1) 对于任意状态s=γ0(s)∈γ*(s),因此有s≤s,自反性可证.
2) 设有状态a和状态b使得(a≤b)∧(b≤a).根据二元关系≤的定义可知b∈γ*(a)和a∈γ*(b)同时成立.当b∈γ*(a)成立,由函数γ*的定义,不妨设b=γi(a),i≥0,带入前提条件a∈γ*(b)有a∈{γi+0(a),γi+1(a),γi+2(a),…,γi+n(a),…},i≥0,因为a=γ0(a),所以仅当i=0时(a≤b)∧(b≤a)满足.此时b=γ0(a)=a,反对称性可证.
3) 设集合γ*(s0)中有状态a,b,c满足a≤b且b≤c,设a=γi(s0),b=γj(s0),c=γk(s0).i,j,k∈N,根据二元关系≤的定义可知,i≤j,j≤k即i≤k,可得a≤c,传递性可证.综上,二元关系≤为偏序关系可证.
4) 集合γ*(s0)中的任意元素均存在γi(s0),i≥0的表达形式,因此任意2个元素总是可比较的.
证毕.
状态迁移函数定义了指令执行前后机器状态的一个二元关系.因此程序在机器上的执行过程可以用全序集{γ*(s0),≤}来表示,其中s0为程序加载完后的机器初始状态.
2.3 模拟行为的抽象
模拟是二级制翻译的核心本质,抽象描述程序执行过程后,就可以对模拟的概念加以阐述.
设源机器MR=(SR,γR)在初始状态s0∈SR执行程序p得到状态有序集合
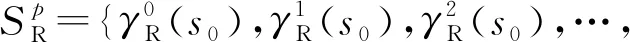
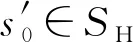
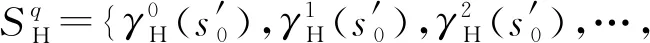
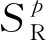
2.4 二进制翻译过程的抽象
二进制翻译最终实现了指令序列到指令序列的映射.根据宿主机器对源机器上程序模拟执行的定义,可以定义二进制翻译:
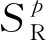
3 二进制翻译的正确性
翻译源机器平台上的程序,是为了在宿主机器平台上得到具有相同逻辑功能的程序.因此翻译得到程序的逻辑功能相同与否决定了翻译的正确性.然而当讨论翻译正确性的时候,需要先统一描述程序的功能,继而给出关于逻辑功能等价的定义,最终探讨正确的二进制翻译过程具有的一般性质.
3.1 等价的一般性描述
程序逻辑功能的等价可以通过相同逻辑功能的正确性证明[13].即通过证明不同程序满足相同逻辑功能的正确性,从而证明程序间在某种程度上具有等价性.
证明程序a,b等价,需要证明对于任意前置条件P和后置条件Q,{P}a{Q}可证当且仅当{P}b{Q}可证.该描述方法借用了程序功能验证描述的一般形式——霍尔三元组,将程序的功能等价定义为功能相同.然而此处定义的前置条件和后置条件是不加限制的.因此,当讨论对象限制在源机器和宿主机器之间的指令序列执行其指称语义的等价,有效的二进制翻译具有如下性质.
性质2.设机器MR到机器MH的正确翻译是指对于MR上任意满足关系(p≤q)∧(p≠q)的状态p,q,在SH上总存在状态满足关系(p′≤q′)∧(p′≠q′)的状态p′,q′与之相对应,可表示为
trans(MR,MH)⟺(∀p,q∈SR.(p≤q)∧(p≠q)⟹ ∃p′,q′∈SH.(p′≤q′)∧(p′≠q′)).
(6)
式(6)中,限制状态p,q不相等,因为对于不改变机器状态的指令进行翻译是没有意义的.性质2和式(6)是对具体程序在不同机器上翻译、模拟性质的推广.因而在此不予证明.通过将源机器和宿主机器抽象为2个偏序集合 {SR,≤}和{SH,≤},翻译过程和程序模拟执行过程被有效区分,有利于二进制翻译正确性的深入分析.
3.2 状态映射函数的性质
在给出二进制翻译正确性的一般性质之后,我们需要对翻译过程所具有的性质进行分析.即为了实现源机器上程序的模拟执行,如何在宿主机器上构建与之相对应的状态序列.

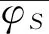
性质3.态映射函数φS是保序映射,单调且存在反函数.
尽管状态映射函数φS作用的对象是源机器的机器状态,然而其本质是对源机器状态集合中的后继关系到宿主机器状态集合中的后记关系的再现.
因此,翻译的正确性体现在状态映射函数φS能否构建一个满足模拟源机器程序执行的状态集在本地的一个模拟实现.
3.3 状态转移函数的表达形式
综合3.2节所述,映射φS描述了状态转移函数γR和γH执行前后状态之间的关系.
根据式(6)可知,满足正确性的翻译过程中所实现的二元关系的映射,是从γR到γH的映射,即从已知源平台的指令序列到不确定的宿主平台指令序列的映射.此时可以用描述机器状态序列所蕴含的指令序列指称语义的函数来描述二进制翻译中映射关系的保持.
状态转移函数γH所描述的前后继关系显然是受γR的描述约束的.根据紧致性定理,若对状态转移函数γR作用域中每个子函数均有对应的状态转移函数满足有效翻译间的映射关系,那么每个子函数映射得到函数的集合所构建得到状态转移函数γH是满足翻译的有效性的.
因此,复杂机器指令的指称语义函数可以使用其子函数指称语义函数集合的形式描述[14].描述翻译过程需要明确状态转移函数的表示形式.根据工程实践中待翻译指令的可确定性,本文将状态转移函数的描述划分为基于子函数的描述和基于连通图的描述2种.
3.3.1 基于子函数的描述
γ={fi(s)},s∈Ai给出了符合机器指令功能描述的状态转移函数表示形式.根据状态转移过程中所执行的指令进行分类,将状态转移函数划分为若干个描述不同指令功能的子函数.其中,{Ai|i∈I}表示对状态转移函数γ在状态集合S上的1个划分.当划分所得的子集数目有限时,根据紧致性定理,如果对于机器状态集S划分的每个子集,状态转移函数γ都有1个有效的子函数,那么状态转移函数γ对于机器状态集S的状态转移关系定义是有效的.
然而这种划分需要对作用的状态先进行关于定义域划分的归类,因此在使用状态函数计算时需要先进行归类计算.
3.3.2 基于连通子图的描述
使用基于子函数的描述方式通常能够较为完备地描述状态转移函数.然而当研究范围局限于部分机器状态时,基于子函数的描述方式会构建大量冗余的关系定义.并且当需要对状态转移函数进行修改且状态后继关系不确定的时候,使用子函数进行描述所定义的状态转移函数更加复杂.
γ={{[γn(si),γn+1(si)]}},si∈Ai给出了符合特定指令执行序列描述的状态转移函数表示形式,其中{[γn(s),γn(s)]},n∈N表示状态s及其所有后继状态作为状态转移函数定义集所定义的后继形成的集合.其现实意义即每个初始状态对应机器执行过程中一个特定的执行序列.
此时可以使用有向图来描述二元后继关系.对满足(a≤b)∧(a≠b)的机器状态a,b,以a为起点、b为终点作有向图.因此,当给定任意状态s时,求解s所定义状态转移图中所有的连通关系,通过求解以s为起点,依次求解每个后继节点的后继,得到1个后继关系图,该图是状态转移状态图的1个连通子图.这种描述则是将机器状态根据后继关系划分成了若干个连通子图.
状态转移函数适合描述待翻译指令具有不确定性的动态翻译过程,因为待翻译指令不确定,机器状态序列间的前后继关系较为复杂,使用子函数能够较好地描述这种复杂的前后继关系;而在可以静态翻译的程序中,分析得到确定的指令序列片段,因此每个指令序列执行前后机器状态的变化较为简单,使用状态连同图描述较为便捷,可以简化新构建的状态转移函数.
3.4 指称语义等价状态序列的构建
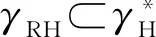
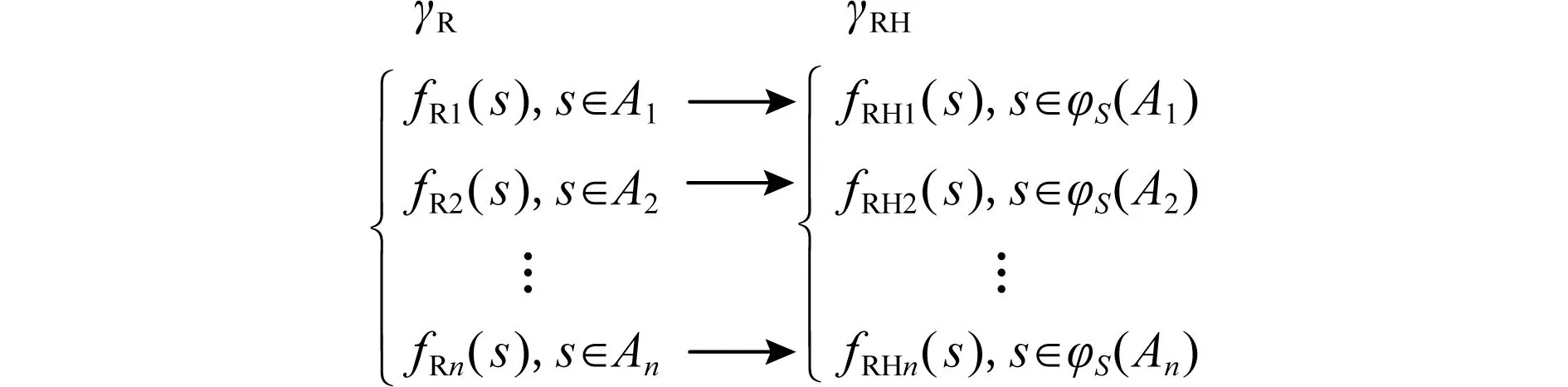
Fig. 2 Construction of state transition function based on subfunction description图2 基于子函数描述的状态转移函数构建
通过这种描述,将状态转移函数γRH的构建问题细化为对状态转移函数γR中子函数fRi(s),s∈Ai对应的状态转移函数fRHi(s),s∈φS(Ai)的构建.因为状态转移函数γR的作用域SR为有限域,其上的划分{Ai|i∈I}也是有限的,选择的划分方式决定了i的值,从而决定了构建状态转移函数γRH的复杂程度.
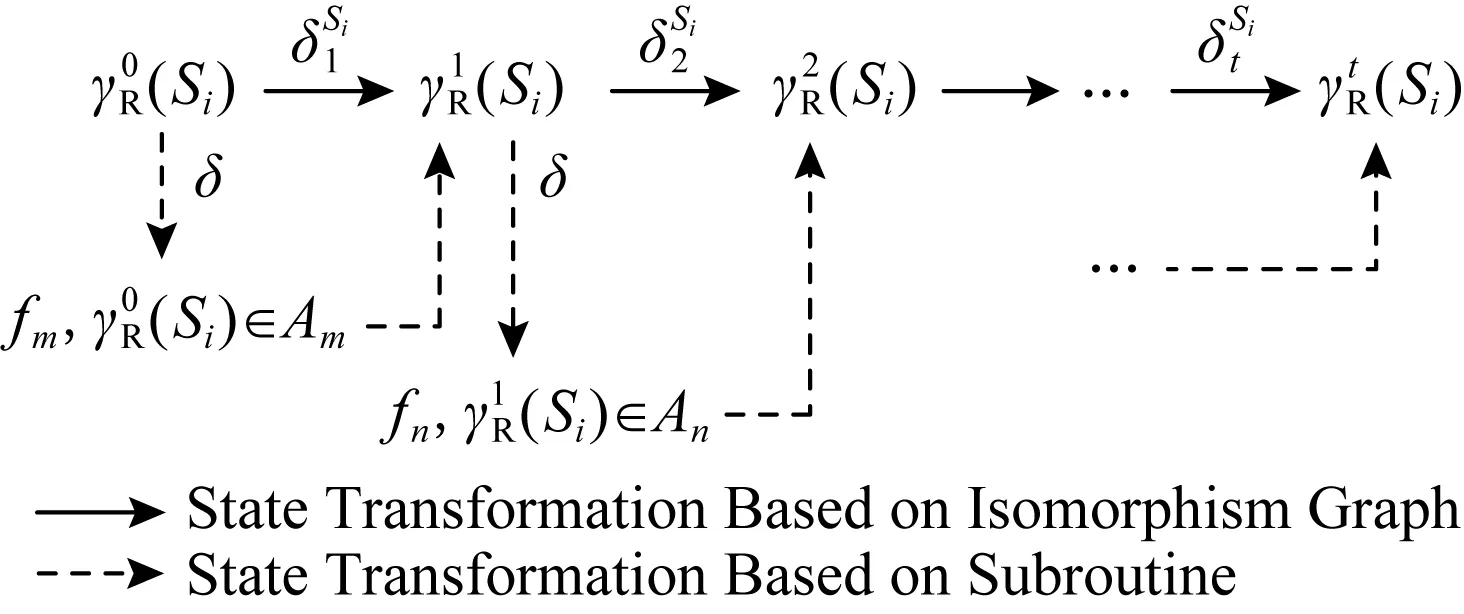
这种描述的现实意义即按照机器状态转移的方式进行分类,从而可以对不同指令的处理过程进行分类讨论.如果γR是基于连通子图描述的,γRH的构建如图3所示:
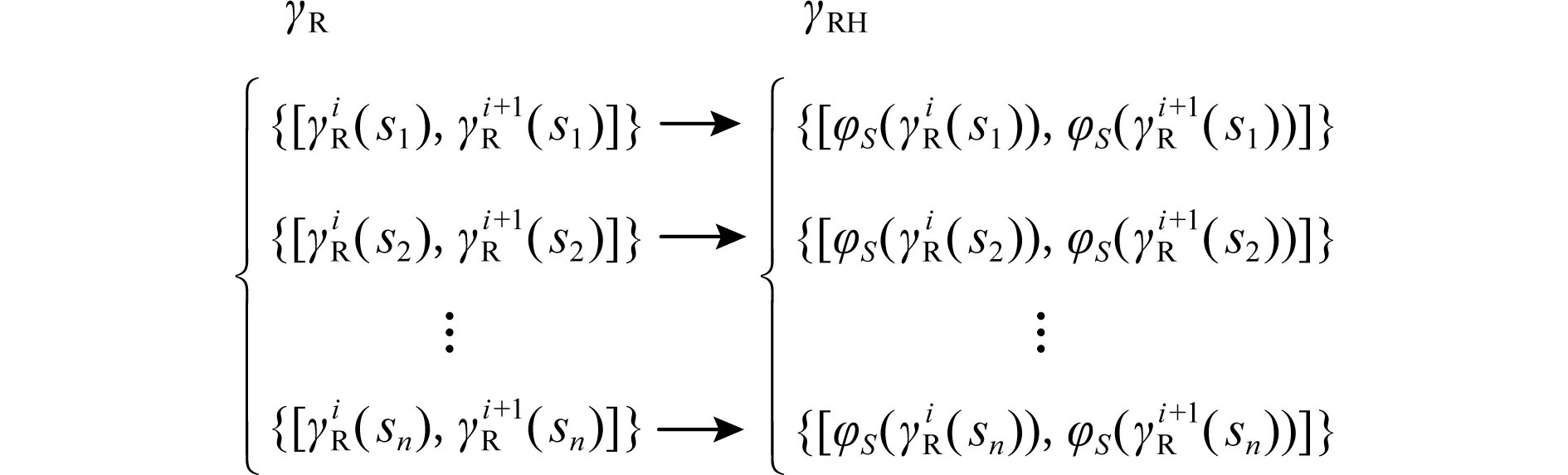
Fig. 3 Construction of state transition function based on connected subgraph description图3 基于连通子图描述的状态转移函数构建
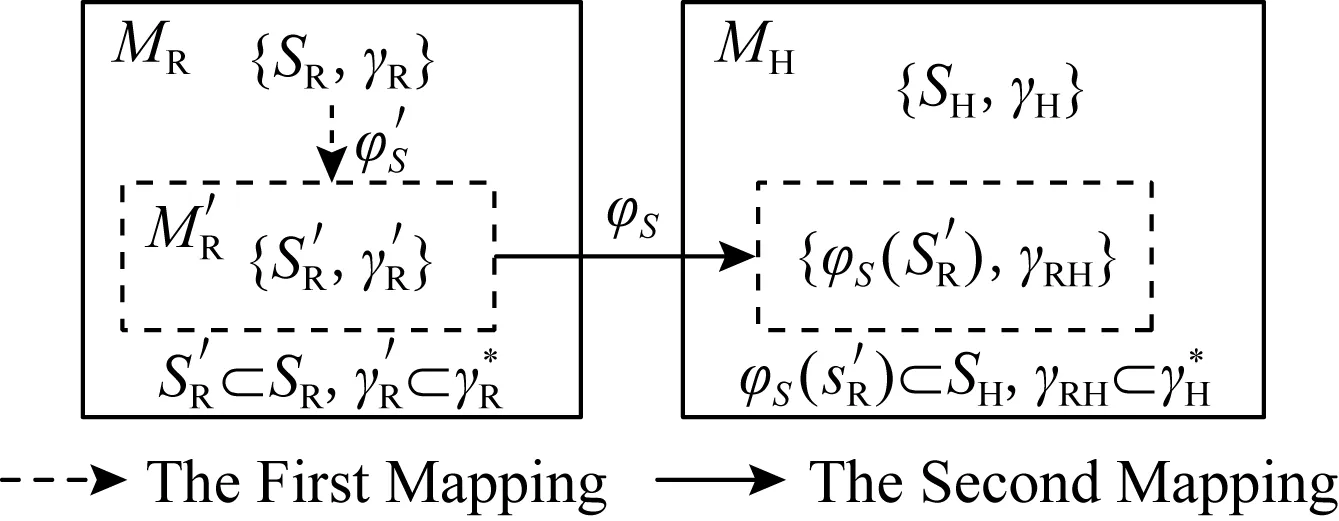
基于连通子图描述的状态转移函数构建过程如图3所示.其中,si∈Ai,0 当在宿主机上构建具有语义等价的指称函数之后,便可以使用代表宿主机指令指称函数的状态转移函数γH去实现构建的γRH,通过γH实现γRH所构建的状态序列若满足和源机器序列语义等价,则满足翻译正确性[13].至此,二进制翻译的形式化模型可以描述如图4所示: Fig. 4 Formal model of binary translation图4 二进制翻译的形式化模型 图4构建了二进制翻译统一的形式化模型,然而在工程实现中,宿主机器状态转移函数构建的正确性验证与翻译器使用的翻译方式是相关的. 动态二进制翻译中代码发现过程与翻译过程是交叉执行的,因此可以处理执行路径较为复杂和不确定的指令序列.处理这种指令序列,使用基于子函数的形式描述源机器指令执行前后机器状态的变化是较为合适的.如翻译器QEMU自带的正确性验证程序test-i386,即通过x86处理器指令的翻译测试验证翻译系统的正确性. 静态二进制翻译中代码发现过程相对于翻译过程是独立的,可以构建待翻译程序的执行路径流图.此时,使用基于联通子图的状态转移函数描述源机器上一段确定指令序列的状态转移函数是较为合适的.静态二进制翻译通常以指令段为基本单位,在翻译的过程中结合语义分析进行优化,最终翻译得到的结果很难使用基于指令翻译正确性的验证方法去验证翻译的正确性.因此,静态二进制翻译通常以翻译后指令最终执行结果作为正确性测试的结果.常用的测试集包括nbench,spec2006等. 本节从状态转移函数不同表述形式的使用、状态转移函数在宿主机器状态序列的实现以及状态转移函数的修改3个方面,阐述各种实现方法对翻译得到的状态序列效率的影响. 翻译后得到的宿主机状态序列,其目标后继状态的计算过程越快,计算执行的速度越好.即生成的指称函数γRH在使用基于γH定义的子函数实现时,其实现的复杂程度越低越好.状态转移函数γ同时也是指令序列的指称函数,具有2种描述形式.因此后续状态的计算形式也有2种. 首先给出使用基于子函数描述的状态转移函数计算后继状态的计算过程. 设γ={fi(s),s∈Ai},0 γi(s)=fm(γi-1(s)),γi-1(s)∈Am. 若将对当前状态归类的过程看作一个函数,该函数以当前状态为参数,查询当前状态在状态转移函数定义域中所属的子域,以该子域对应的子函数为返回值.设δ为状态归类函数,δ(s)=fi,s∈Ai,则基于子函数表示的状态转移函数γ计算后继状态γ(s)的计算过程可表示为 (7) 式(7)中状态归类函数δ是一个关于γi-1(s)的二阶函数.该函数抽象描述了基于子函数表示的状态转移函数做后继状态计算的过程,忽略了状态转移函数的表示形式,可以将任意起始状态s0的后继状态的计算递归地表示为 用δi=δ(γi-1(s))表示第i次后继状态计算的状态转移函数,则后继递归计算递归地表示为 此时状态转移函数定义了由若干状态子集划分的后继关系集合γ={δSi,δSj,…},其中状态集合Si,Sj是状态全集S的1个有效划分中的不同元素. 由此可见,在针对部分指定状态的后继计算过程中,使用基于子函数表示的状态转移函数与使用基于连通子图表示的状态转移函数具有一致性. 性质4.设有状态集合Si,如果其在源机器状态转移函数中有基于连通子图的定义,那么,在宿主机上构建状态转移函数时,针对状态集Si的映射状态φS(Si) 构建的状态转移函数,基于连通子图构建的状态转移函数效率会比基于子函数构建的状态映射函数效率高. 性质4的证明需要通过分析图5中使用2种不同状态转移函数计算后继状态的复杂程度. Fig. 5 Subsequent state calculation progress (1)图5 后继状态计算过程(1) 在实际应用中,动态翻译在运行时翻译和维护代码的过程实现了模拟状态转移指令序列的生成,但从功能上并没有实现模拟源平台状态的转移,所以执行效率低于静态翻译.与此同时,也显示出了静态翻译的局限性,因为需要预测源机器执行的状态序列. 将指令及其解释函数抽象为状态转移函数,能够对二进制翻译过程进行更系统的刻画,主要是可以对机器模拟、动态翻译和静态翻译进行统一描述.而这种形式化的统一描述对于构建动静结合的二进制翻译模式是至关重要的. 在二进制翻译模型中,基于偏序集{SH,γH}翻译得到了偏序集合{φS(SR),γRH}.因此在实现γRH时,所使用的状态序列是需要满足γH所定义的后继关系限制的.这种限制体现在宿主机器体系结构特征对二进制翻译结果的限制. 这种限制形式化描述为:若γH={f1,f2,…,fn},那么γRH=f…(…fj(fi(s))…),s∈SH. 现实中,任何机器平台最终只能执行该平台所能识别的指令和操作.基于子函数描述的状态转移函数γH抽象了宿主机器的体系架构,定义了一系列的功能(指令).由此可见,不同指令序列所对应的状态序列会影响γRH中后继状态计算的效率.这种影响和具体的机器架构相关,不做过多讨论.这种优化方式在应用中主要体现为寄存器映射一类的优化方法中,将源平台上使用频繁的存储单元(通常为寄存器)映射到宿主平台的寄存器上.因为使用频繁,节省了映射在内存中反复读写而占用的时间[17-18]. 在二进制翻译中,有时为了获取更高的效率,会忽略宿主机器翻译执行过程中的部分状态是否与源机器的执行状态相互对应、而只是关注在部分关心的状态节点是否能够相互对应.这种忽略源机器执行序列过程,而只在意部分节点对应的方法,是在具体问题中对源机器所定义的偏序集{SR,γR}进行了修改、在删减部分不关心的状态之后,并使用其前驱元素和后继元素构建成新的状态转移函数,如此提高后继状态的计算速度.经过这种修改后,在宿主机器得到的执行状态序列与源平台的状态序列其对应关系不再严格满足,此时式(6)中关于正确性的描述是不成立的.为了使得翻译中正确性和优化带来的影响能够有区别的讨论,因此对二进制翻译的模型修改如图6所示: Fig. 6 The quadratic mapping process of binary translation图6 二进制翻译双映射过程 删减状态元素有利于降低问题的复杂程度,忽略一些不关注的机器状态及其处理过程.在现实中,根据用户的需求和关注的对象,如进程级的翻译系统在操作系统层及其以下做了本地虚拟化的处理,忽略了一些底层实现的翻译,而在软件无源移植的过程中相较于系统级的翻译系统具有巨大优势. 然而此类优化是基于对具体问题的求解需求进行分析的.处理方法是将不关心的过程的起始状态及其终止状态进行界定,为了保证问题讨论的完备性,对起始状态进行划分,划分的依据即对于问题的具体讨论,然后根据专业知识构建起始状态每个子类到终止状态的状态转移函数. 图7中使用优化后的基于状态集与状态转移函数描述了后继状态的计算过程,使用该方法形成的状态转移函数同时使用了基于子函数以及基于同构图2中状态转移函数的表示方法. Fig. 7 Subsequent state calculation progress (2)图7 后继状态计算过程(2) 不同于图5中逐单条源指令后继状态的变换以及后继转移函数的推导,图7中计算状态Si的子集 在软件移植的应用中,对应用程序的主体采用动态的二进制翻译技术,对程序执行所依赖的过程函数,根据函数的特性,可以不做任何处理,模仿源平台调用过程的动态翻译;也可以根据函数说明,分析参数传递,做本地函数封装调用的替换处理;也可以对依赖的自定义库函数进行静态翻译成本地库函数,再封装调用替换.在上述相关工作中,特别是库函数的替换处理以及库函数的静态翻译,对该模型的性质进行了验证. 二进制翻译技术在体系结构优化、程序性能优化、安全性分析以及软件移植的研究中具有重要作用. 本文首先分析了基于指令解释的映射模型在二进制翻译关于正确性以及翻译效率研究中的不足,给出了基于后继关系的映射模型;继而定义了正确翻译并形式化地描述了正确翻译的过程;最后就翻译过程汇中翻译效率的优化方法分别进行了讨论. 在分析翻译正确性和翻译优化方法的过程中,结合实际也对翻译正确性的性质以及翻译优化方法的效果进行了论证.并在最后指出了二进制翻译研究中的热点以及难点——动静结合的二进制翻译模式. 本文所论述的二进制翻译中的正确性以及优化方法的形式化也是该翻译模式研究的基础.针对如何通过动静结合的二进制翻译模式有效提高二进制翻译技术的实用性将作为下一步的研究目标.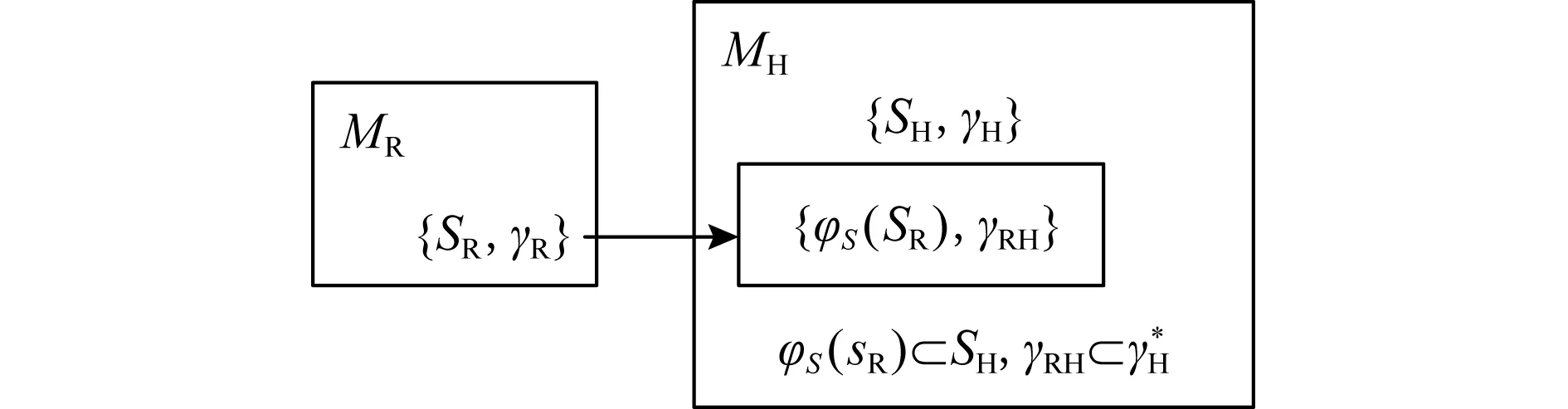
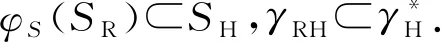
3.5 状态转移函数构建的正确性验证
4 优化过程的形式化描述
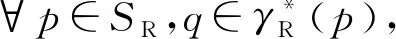
4.1 状态转移函数表述形式对效率的影响
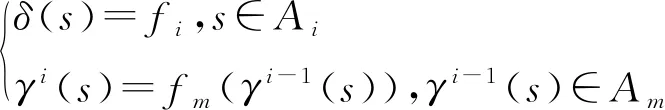
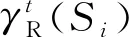
4.2 状态转移函数在宿主机器状态序列的实现
4.3 状态转移函数的修改
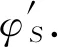
4.4 复合优化翻译模式

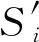
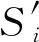
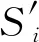
5 总 结

