基于高斯分布的密度误差对航天器轨道的影响分析∗
刘卫,刘四清,龚建村,王荣兰
(1.中国科学院国家空间科学中心,北京100190;2.中国科学院微小卫星创新研究院,上海201210;3.中国科学院大学,北京100049)
1 引言
自1961年美国子午仪-4A卫星在轨爆炸以来,可观测空间碎片数量出现大规模增长[1]。1978年1月,入轨仅3个月载有核反应堆的宇宙954卫星再入时,在加拿大上空失控,沿约1000km的区域释放了约30kg核辐射物[2]。1996年7月,法国樱桃卫星被1986年11月阿里安火箭爆炸的碎片撞击损坏[3];2009年在用卫星美国铱星33和俄罗斯宇宙2251发生碰撞,产生可追踪碎片超过2000块[4,5];1989年3月的太阳大爆发造成了大量太空编目目标的丢失,2012年7月美国空间监视网 (SSN)更是创下目标丢失列表纪录[6,7],原因也正是太阳活动峰年的热层大气模式误差。近年来空间目标频繁发生在轨碰撞,陨落进入地球大气烧毁,甚至砸至地面,对人类的空间资产和地面安全造成威胁。热层密度预测值的不确定性造成的空间碎片的轨道衰减,对碰撞发生时间和位置的预测有很大影响[1]。碰撞预警计算中漏警、虚警时有发生,陨落预报中误差较大等这些问题都是热层大气密度预测误差直接或间接造成的。20世纪50年代末,第一颗人造卫星上天后观测到大气阻力对卫星轨道运动的影响。基于卫星轨道衰变数据,Jacchia等人在20世纪60~70年代开发出第一代通用经验大气模型,如HarrisPriester、Jacchia模型[8]。经过数十年发展,目前已有Jacchia、DTM和MSIS等系列热层大气密度模式,这些模式平均而言,均存在15%~20%的误差,空间环境扰动期间误差甚至超过100%[9,10],无法满足空间态势感知等高精度的军事需求。
Travis等人利用CHAMP和GRACE精密星历(POE)估算大气密度,评估大扰动期间的密度变化,发现使用POE推导密度与加速度计反演密度预测的轨道之间的误差很小。因此Travis认为加速度计观测到的热层密度高频变化项,对轨道分析应用都不重要[11]。大气阻力可以从近地轨道卫星的轨道信息中推断出来,为测量质量密度提供了一种直接的手段。CHEN等人基于半长轴的阻力摄动方程,使用CHAMP卫星反演密度,发现应用反演密度可以减少轨道预测误差[12]。Rodney等人通过2003~2007年期间CHAMP卫星加速度计数据,验证密度模型延时误差的影响,并分析延迟对轨道预测结果的影响[13]。
在热层大气模型性能评测中,通常给出相对误差标准差,如15%~20%,而忽略误差均值问题。那么热层大气密度模式误差的统计特性上是否为零均值,非零均值如何影响航天器轨道预报,标准差又是如何影响轨道预报的呢。典型热层模式误差及对轨道预报影响的相关文献多见报道,但未见文献给出上述问题答案。本文通过热层模式误差特性的统计和轨道预报数值试验,将给出上述问题的答案。期待为热层模式的轨道预报应用改进、建模指引方向。
2 模式误差特性
从热层大气建模的角度来看,热层模式不应存在系统性偏差,也就是相对误差均值不为零的情况。由于空间环境变化极其复杂,累积的热层密度探测资料在时间空间上存在不连续、分辨率低等情况,目前热层大气的部分变化机制仍不确定。目前的热层大气模式在不同空间环境下表现出差异化的系统偏差。
2.1 模式长期特性
热层模式的长期特性是指大时间尺度 (太阳活动周)上表现出来的偏差、标准差等性质。
为定量评估动态改进前后模式性能,我们定义模式偏离实测的百分比,即相对误差ε:
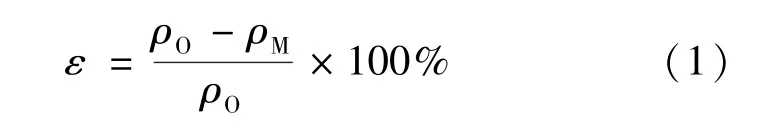
式中,ρO,ρM分别是密度实测值和模式值。
PARDINI等人通过分析四颗卫星半长轴衰减,评估了JR-71、 MSIS-90、 MSISE00、 GOST-2004、JB2006和JB2008六种大气模式,指出由于建模时采用高度无关的固定值阻力系数,此六种大气模式均高估500km以下大气密度约7%~20%[14]。平均偏差最小的模式依次是 JB08、MSISE00和GOST-2004。同时给出了第23太阳活动周峰年各模式在不同高度的平均偏差,见表1。
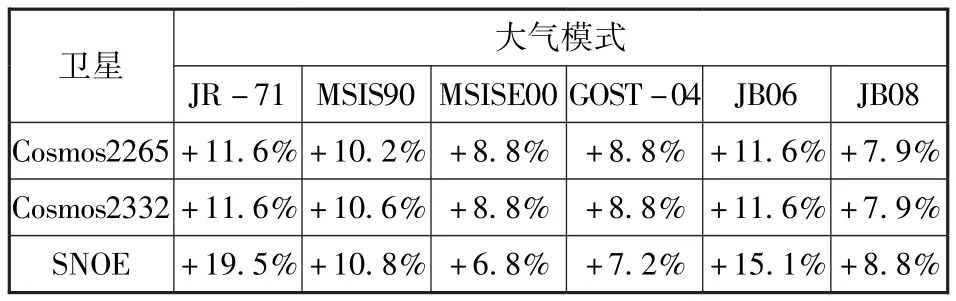
表1 各模式不同高度的平均偏差Tab.1 The mean bias of different models
刘卫等人基于CHAMP卫星2001年5月15日至2008年12月31日期间加速度计反演热层大气密度数据为基准,对JB2008和MSISE00两模式误差进行统计分析[15],给出了 JB2008和MSISE00两种模式在不同类型的空间环境下,相对误差均值、标准差的特性,如表2所示。
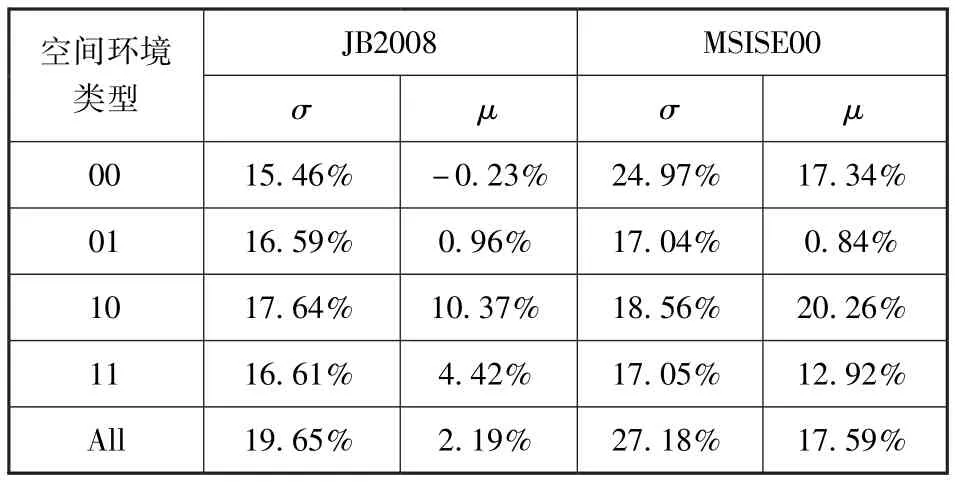
表2 两大气模式相对误差均值与标准差@400kmTab.2 The mean relative error and standard deviation at 400km altitude
由上述统计分析表明,长期而言典型模式误差均值仍不为零,并且在不同空间环境、高度表现也不同。
2.2 事件期间的模式特性
空间环境事件期间的模式特性是指小时间尺度 (几天)上,发生空间环境扰动事件时,热层大气模式表现出的误差特性,包括误差均值和标准差。图1是基于CHAMP加速度计反演热层密度,以日为区间单位统计给出的MSISE00模式的相对误差均值和标准差随太阳活动指数F10.7和地磁活动指数Ap的变化情况。图中可见MSISE00模式相对误差均值μ和标准差σ,随空间环境变化,几次磁暴均存在μ和σ陡增,μ达到100%,σ甚至可以达到300%。
图2给出2003年10月31日磁暴事件期间JB2008和MSISE00模式相对误差分布。图2可见,JB2008相对MSISE00模式误差分布更集中,数据统计两模式在该磁暴事件期间的相对误差均值分别为48%和75%。
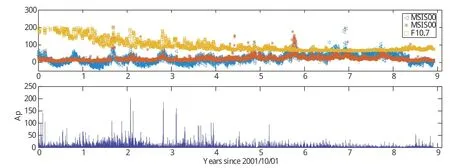
图1 MSISE00模式相对误差均值和标准差随空间环境的变化Fig.1 Variation of mean and standard deviation of MSISE00 model error with space environment

图2 2003年10月31日磁暴事件期间JB2008和MSISE00模式相对误差分布图Fig.2 Relativeerror distribution of JB2008 and MSISE00 models during the 2003/10/31 event
由上述统计可见,无论是热层模式的长期特性还是空间环境事件期间的模式特性,热层大气模式误差均值和标准差都不为零,空间环境事件期间表现更加明显。
3 轨道预报影响统计
3.1 轨道预报
CHAMP卫星的快速科学轨道 (Rapid Science Orbit,RSO)数据具有较好的连续性,且轨道位置精度优于10cm[12]。我们以CHAMP卫星采样间隔30s的RSO星历数据为参考轨道,对轨道预报结果进行比较分析,轨道预报中的主要模型和参量:
(1)99×99阶地球引力场模型GGM05C;
(2)30×30阶TOPEX 4.0海潮模型;
(3)CHAMP加速度计反演大气密度;
(4)坐标、时间及天文常数系统采用IERS(2010)标准;
(5)日、月引力摄动;
(6)太阳光压,固体潮摄动。
3.2 高斯分布误差
符合高斯分布误差产生同样是模式误差如何影响轨道分析的关键。我们的高斯分布误差产生是基于两个均匀分布随机变量的组合获取的,具体理论如下。如果x1,x2… 是具有联合概率分布p(x1,x2…)dx1dx2…的随机偏离,并且如果y1,y2…每个都是所有x的函数,则y的联合概率分布为:
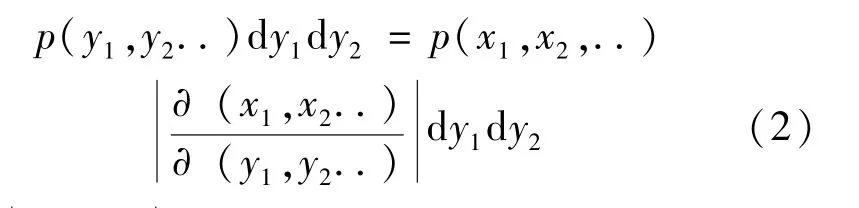
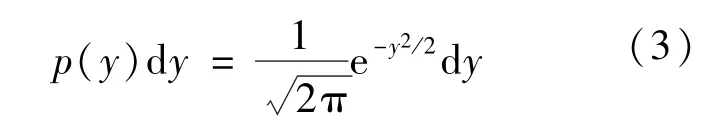
考虑 (0,1)内两个一致偏离x1,x2与两个变量y1,y2之间的变换:
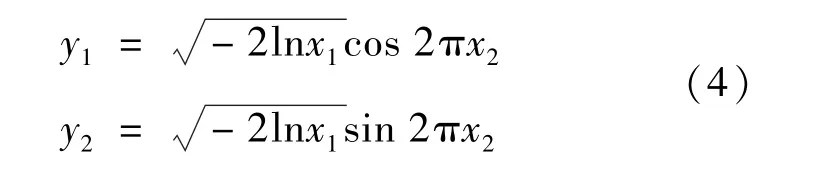
等价地可写成:
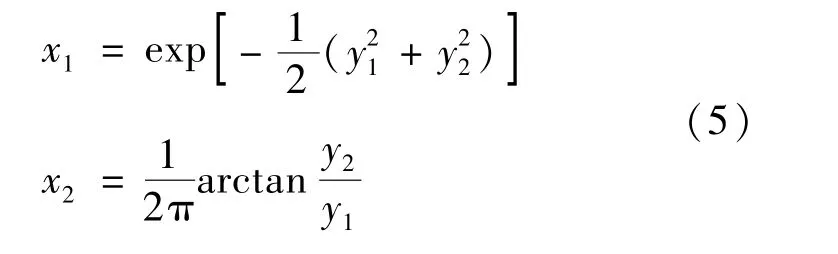
雅克比行列式可以如下计算[16]:
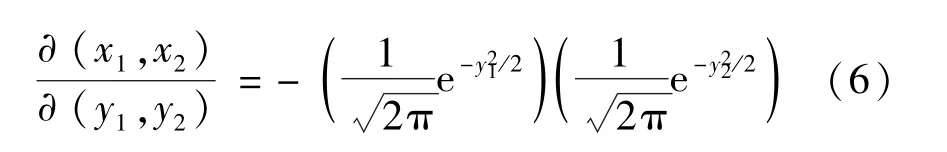
上式是y1函数与y2函数的乘积,都独立服从正态分布。这是符合 (0,1)高斯分布的随机变量y,那么任意(μ,σ)高斯分布的随机变量y′可如下获取:

图3是实际仿真计算中产生的高斯分布随机误差,图3中 (a)、(b)、(c)设定的均值和标准差分别是:30%、100%;30%、50%;10%、80%;实际产生的误差均值和标准差分别是:29.08%、98.68%;29.54%、49.34%;10.74%、78.94%,符合要求。
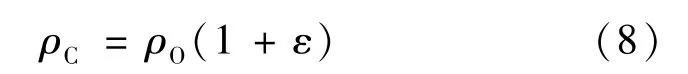
式中,ρC,ρO分别是计算中使用的密度值和密度实测值。高斯分布随机误差由上述公式产生后,按照式 (8)计算热层密度,进行轨道预报并统计预报误差情况。
4 结果分析
前节模式特性分析可见,空间环境事件期间热层大气模式存在较大的误差均值和标准差。因此空间环境扰动期的航天器轨道预报是航天工程应用的痛点问题。我们以3h值ap≥236为条件筛选出2001~2010年期间,具有CHAMP轨道数据的16个磁暴事件,见表3。施加符合不同均值和标准差的高斯分布热层密度误差,分析轨道预报误差。发现16个磁暴事件中,在相同误差参数下,轨道预报特性相似,下面选取几个典型事例进行展示分析。
4.1 相同均值的比较
以2003年10月29日磁暴事件为例,在轨道预报中,分别施加误差均值μ=0%,-10%,-30%,10%,30%,每种误差均值下又结合不同的误差标准差σ=0%,10%,30%,50%,80%,100%进行轨道预报误差统计。图4展示的是相对误差均值相同,不同标准差下轨道预报误差。图中相同均值下,轨道预报误差对标准差的变化不敏感,随标准差的增大有所增加。整体上轨道预报误差随误差均值绝对值增加而迅速增大,均值的正负决定预报偏差的方向。
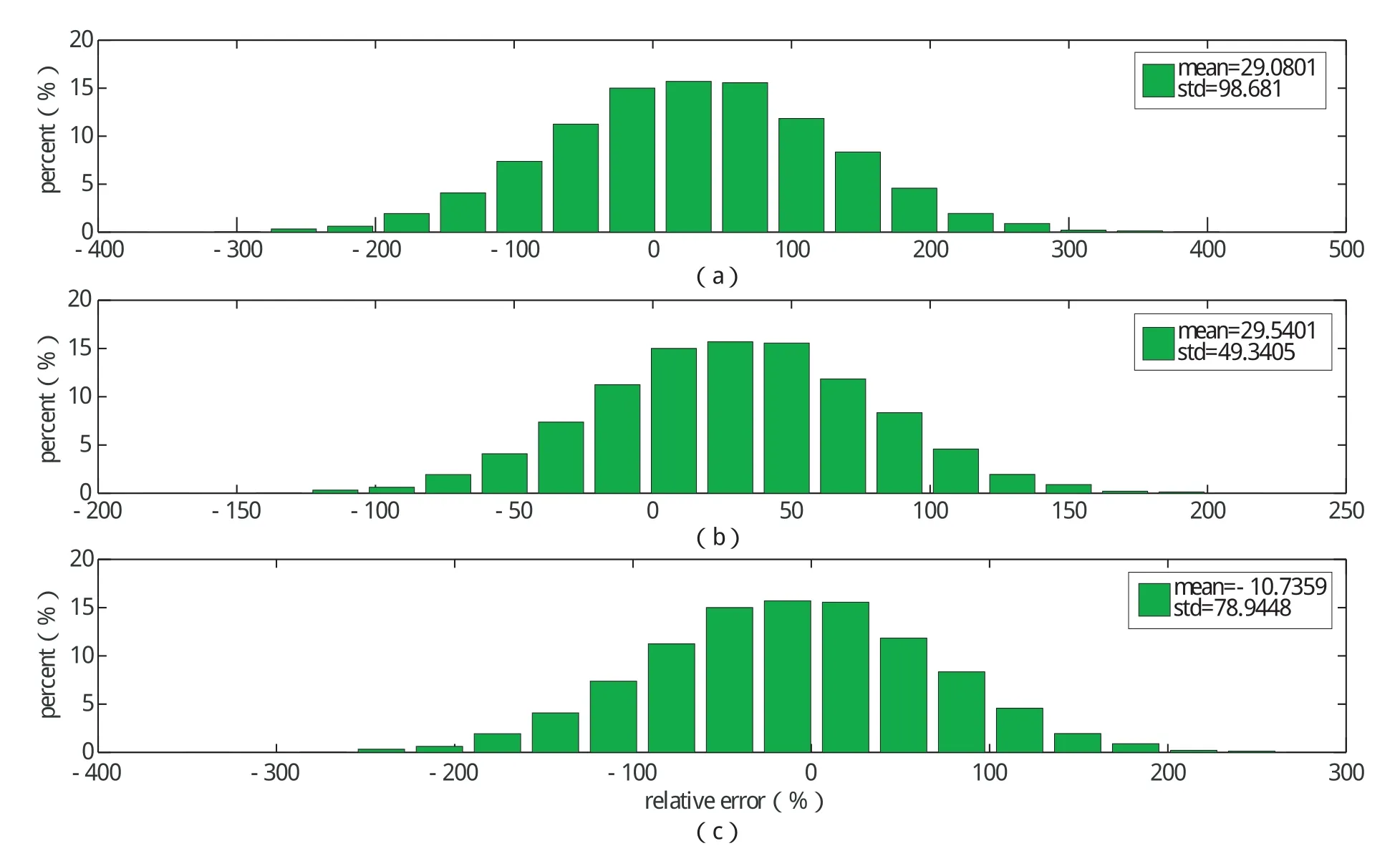
图3 实际产生的高斯随机误差分布图Fig.3 Actual Gauss random error distribution
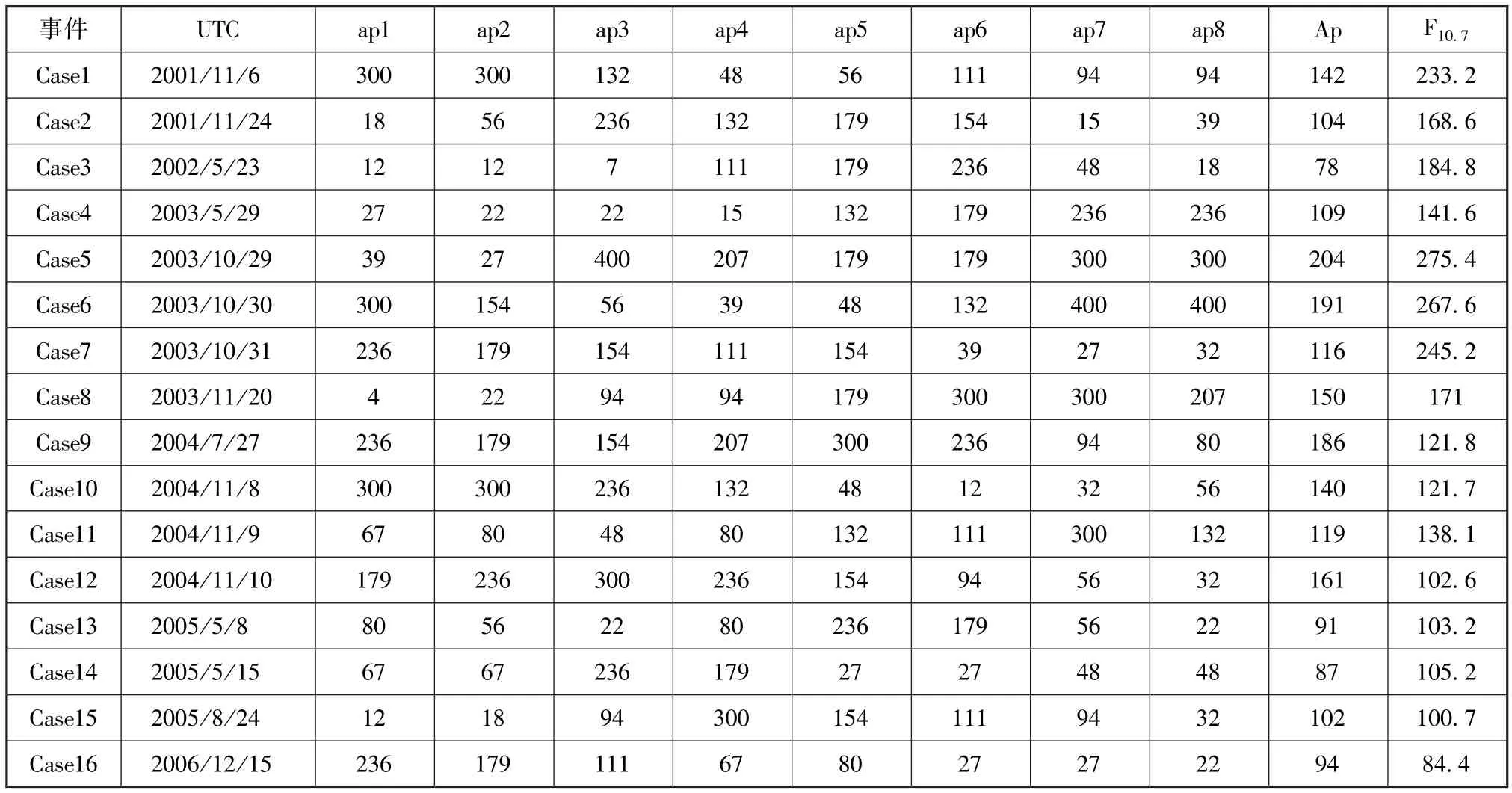
表3 筛选的空间环境事件信息Tab.3 The selected space environmental event information

图4 不同相对误差标准差下轨道预报误差 (均值0%,-10%,-30%)Fig.4 Orbit prediction errors(mean values 0%,-10%,-30%,10% and 30%)under different relative error standard deviations
4.2 相同标准差比较
以2003年10月30日磁暴事件为例,在轨道预报中,分别施加误差标准差σ=10%,30%,50%,80%,100%,每种相对误差标准差又结合不同的均值μ=0%,-10%,-30%,10%,30%进行轨道预报误差统计。图5、图6展示的是相对误差标准差相同,不同均值下轨道预报误差。与上节结果一致,轨道预报误差主要取决于误差均值绝对值,对标准差的变化不敏感。误差均值的正负决定预报偏差的方向,同时证明轨道预报结果对热层小尺度的变化不敏感,热层密度误差可以通过平均进行补偿。
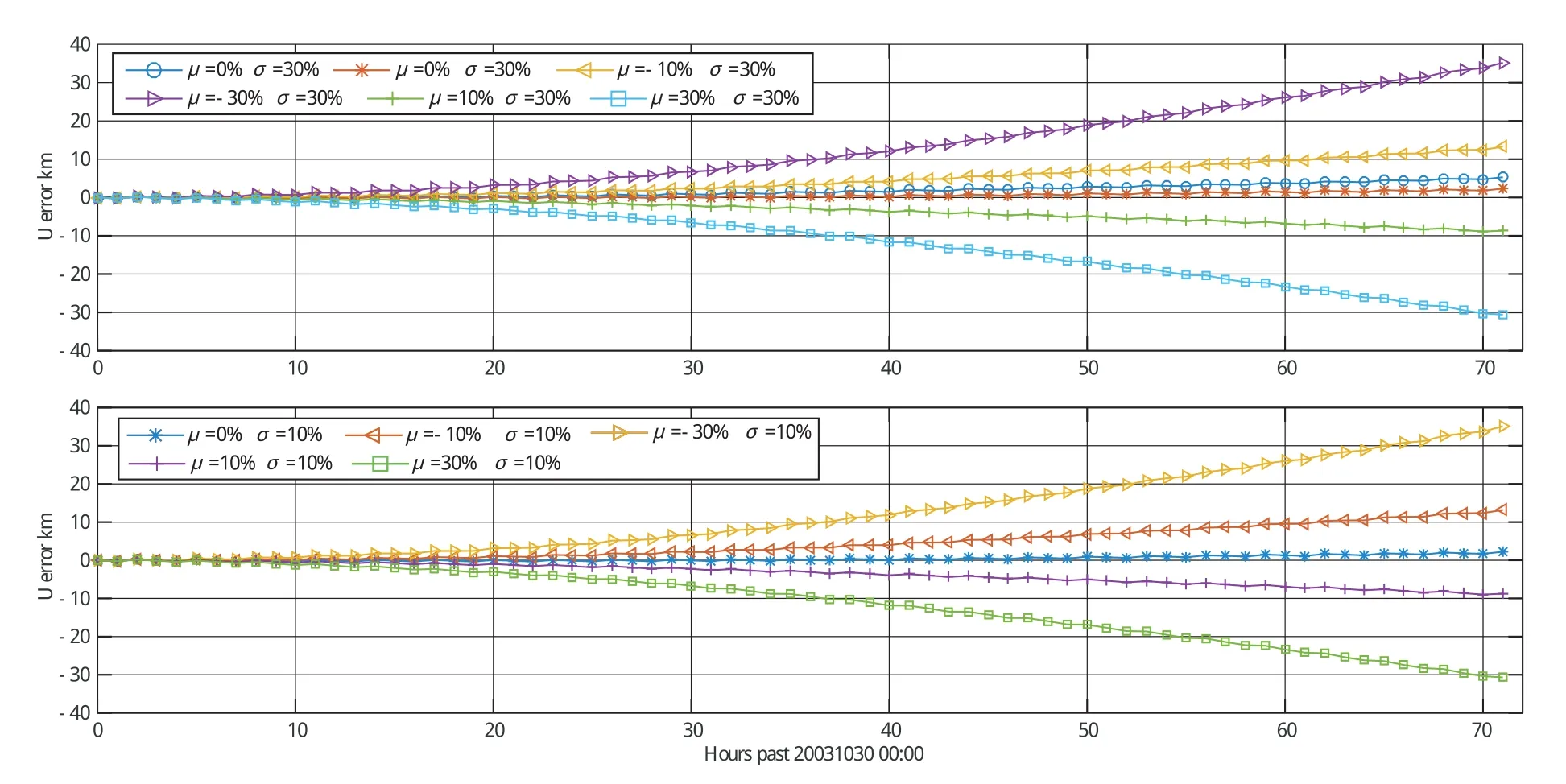
图5 不同相对误差均值下轨道预报误差 (标准差10%和30%)Fig.5 Orbit prediction errors(standard deviations 10% and 30%)under different relative error mean values
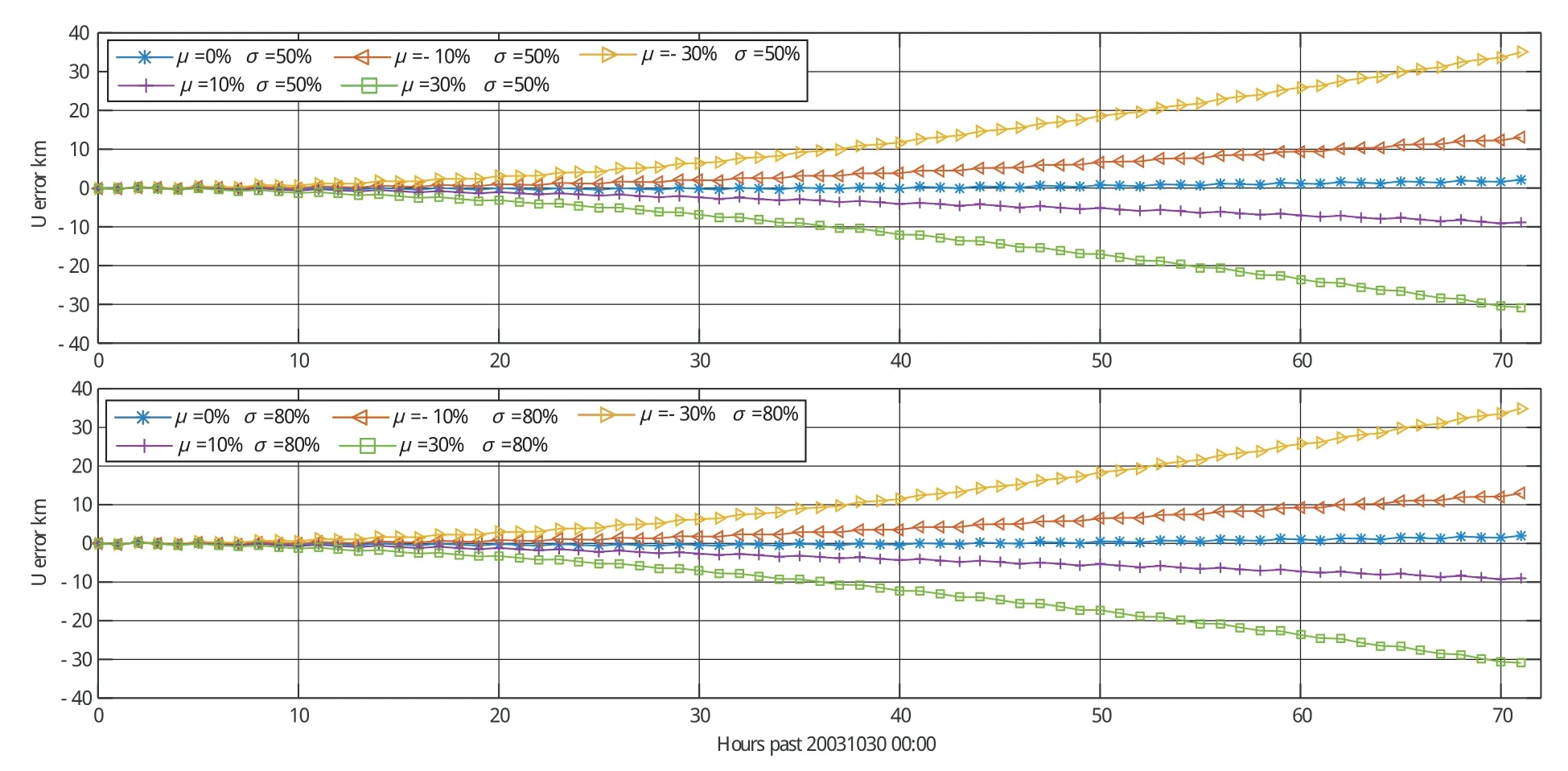
图6 不同相对误差均值下轨道预报误差 (标准差50%和80%)Fig.6 Orbit prediction errors(standard deviations 50% and 80%)under different relative error mean values
5 结论
本文介绍基于高斯分布的密度误差对航天器轨道的影响分析的必要性,统计典型热层模式误差的长期特性和空间环境事件期间模式误差特性,给出航天器轨道预报中引入高斯分布热层密度相对误差的方法,并进行验证。筛选出2001~2010年期间,具有CHAMP轨道数据的16个磁暴事件,施加不同均值和标准差的高斯分布热层密度误差,分析轨道预报误差。得到的主要结论如下:
(1)热层大气模式存在非零均值误差,且该误差随空间环境而变化;
(2)典型热层模式误差均值和标准差,在空间环境扰动期最大可超过100%;
(3)轨道预报误差主要取决于热层模式误差均值的绝对值,对误差标准差不敏感,误差均值的正负决定预报偏差的方向;
(4)轨道预报结果对热层小尺度的变化不敏感,热层密度误差可以通过平均进行补偿。
期望本文对热层大气模式改进、建模具有方向指引意义。

