低地球轨道初轨确定误差分析

杨志涛

(1.中国科学院国家天文台,北京100012；2.中国科学院大学,北京100049；3.国家航天局空间碎片监测与应用中心,北京100012)

1 引言

初轨确定已有200多年的历史，最初是针对小行星、彗星等自然天体，随着天体力学的发展，特别是近代观测技术的发展和计算条件的改善，初轨计算方法也有了进一步发展。人造地球天体上天后，跟踪测量方式有所改变，初轨计算方法又根据卫星运动规律进行诸多改进。但无论何种改进，基本上归结为采用的动力学条件和表现形式的不同，而初轨确定的基本原理并无改变。虽然方法众多，但从本质上讲，初轨计算方法基本上可以分为两大类[1-13]:一类以Laplace方法为代表，通过计算得到t0时刻的位置矢量r0和速度矢量，然后转换成相应的轨道根数；另一类以Gauss方法为代表，通常分为两步，第一步通过计算得到两个时刻的位置矢量r1和r2，第二步由r1和r2计算轨道根数，实即兰伯特 (Lambert)问题。

尽管初轨确定方法众多，但其基本前提是一致的:建立在无任何先验信息前提下的定轨方法[14]。短弧初轨确定的初衷就是在第一次获得该“新”目标的短弧资料时，在没有任何初始信息的前提下确定其轨道。在航天器发射初期和中途修正、对非合作目标和空间碎片的搜索发现或者编目中断后的重新编目等工作中，初轨确定方法都有重要的应用价值。在具体的工程应用中，初轨确定的定轨误差与资料误差的关系是需要重点关注的一个问题。

本文首先介绍了改进的Laplace方法初轨确定的原理，然后利用仿真观测数据对定轨误差与观测资料时长、资料误差及资料密度等因素的关系进行了定量分析，最后总结给出一些有益的分析结论，期望能为相关工作提供技术参考。

2 改进的Laplace法初轨确定原理

2.1 动力学关系

在地心天球坐标系中，航天器相对中心天体(质心)的运动微分方程即:

式中，GM是中心天体引力常数；加速度Fε表示中心天体质心引力以外的各种摄动力。在采用短弧情况下 (这也正对应初轨确定的实际背景)存在如下时间 (间隔)幂级数解:

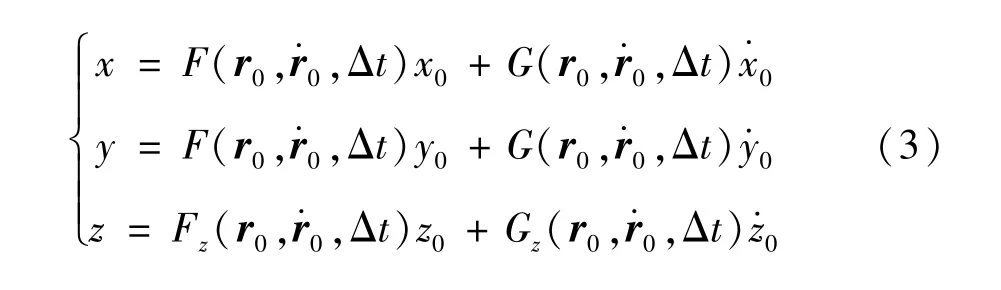
式中，x，y分量的系数相同，在方程中即记作F，G，而z分量就是方程中的Fz，Gz。若记τ=Δt表示时间段长度，则上述系数F，G和Fz，Gz按τ的幂级数展开式如下:

护理床是行动不方便的病人在住院或居家护理时使用的病床．其主要目的是便于护理人员进行照顾，使病人康复．但是传统护理床价格昂贵，而且功能模式单一，或是只能辅助翻身，或是只能辅助坐卧，而且病人一旦需要离开床体进行其他活动时，搬移病人便成了护理人员的一大难题[1-3]．

2.2 基本方程

雷达是空间碎片监测中的常用设备，每次采样可同时获得测距和测角资料(t；ρ，A，h)。对于合作目标的监测，可由卫星导航系统给出每个采样时刻的定位资料t，r(x，y，z)。这两类资料在定轨方程中本质上相同，由测距和测角资料(t；ρ，A，h)结合测站坐标可转换得到同一时刻定位资料t，r(x，y，z)， 相应的定轨基本方程可直接表达为下列简单形式:

对于一次测量采样资料，上式对应的三个方程都是独立的，原则上只需要两次采样即可定轨，给出定轨历元t0时刻的位置r0(x0，y0，z0)和速度

2.3 最小二乘估计

关于上述线性方程组的求解，对于测角加测距或定位资料尽管只要两次采样就可定轨，但通常都是尽量利用多组资料定轨。k次采样数据对应的基本方程个数是k×3，且往往有k×3≥n的状态，这里n=6是轨道量的维数。为了充分发挥多资料的作用，就需要选择相应的最优估计方法来求解定轨基本方程。但对于初轨确定而言，没有必要采用过于复杂的估计方法，通常就采用简单的等权最小二乘估计。

k组数据对应的基本方程组可整理为如下形式，其中

式中， 系数矩阵A3k×6和B3k×1由式 (5) 中的F，G，Fz，Gz等量组成。采用等权最小二乘估计方法可得 到:Z=[(A3k×6)TA3k×6]-1(A3k×6)TB3k×1。由于系数矩阵的计算亦会涉及用到变量Z，因此实际计算是一个逐渐迭代收敛的过程。F，G等量可采用如下初值在定轨中进行迭代，并且这是一个较好的初始信息。

3 初轨确定误差分析

本节分析所用的初轨确定算法，即上文所述考虑J2项影响的改进的Laplace方法；而分析采用的观测资料默认为等时间间隔的多组数值仿真的定位数据。由于初轨计算通常是半长径的误差Δa最大，因此本文以Δa的大小作为衡量定轨结果优劣的标准，下文所述的定轨误差均默认是指Δa。

除定轨模型外，初轨确定的误差还和所用观测资料的情况密切相关，例如资料时长、资料密度以及资料误差的大小。有必要说明，此处的资料时长是指所用资料的最大时间间隔，以此表征资料弧段的大小；资料密度表征所用资料的稀疏程度，由该等时间间隔的长度表示。由上节所述原理可知，此初轨确定方法的核心是在动力学关系中采用了时间幂级数解 (这与通常的轨道分析解中采用的小参数幂级数解有所不同)的形式，表达式的收敛性及精度主要对时长τ(等效于弧长)比较敏感，这与轨道半长轴密切相关，而对其他轨道参数并不敏感，因此本文仿真分析的低地球轨道只涉及不同轨道高度的情况，并未对轨道偏心率和轨道倾角等参数增加算例。

本节主要针对定位资料，分析对低轨不同高度下近圆轨道的定轨误差与资料时长、资料密度以及资料误差大小的关系。分析所用的观测资料由高精度数值法轨道预报软件模拟计算给出:轨道外推的起始历元为2007年7月1日12时0分0秒，终止历元为2007年7月2日12时0分0秒，时间间隔为1s，模拟的轨道共有4组，轨道初值如表1所示；计算时考虑的摄动力模型包括:非球形引力 (20×20阶次)、日月第三体质点引力、大气阻尼、光压和日月潮汐形变摄动等，其中大气阻尼和光压摄动的计算中所用的卫星有效面质比均为0.02m2/kg，大气模型为Jacchia-Roberts。

在下文分析中对观测数据加入的随机误差，采用均值为0、标准差大小为σ的高斯分布的随机数，其中σ会给定不同的数值，并以此表征误差大小。

3.1 定轨误差与资料时长的关系

定轨结果与所用观测资料的弧段大小，即资料时长ΔT密切相关。此处取定轨历元为模拟资料起始历元开始的第500s，即2007年7月1日12时8分19秒；选取数据时固定资料密度为每5s取一点，同时保证定轨历元为所选弧段的中间时刻，资料时长从10s(即3点)开始递增，至定轨误差为Δa=10km时停止，比较的标准是模拟资料中定轨历元的轨道根数。对四条轨道均用上述方法计算，得到定轨误差与资料时长的变化关系如图1所示:

表1 模拟资料轨道初值列表Tab.1 Initial orbital values of simulated data

图1 定轨误差与资料时长关系图Fig.1 The relationship between orbit determination error and data duration

由图1可以看出，定轨误差为Δa随资料时长ΔT变化的总体趋势相同:在ΔT较小 (100s内)时Δa会有小幅波动，随着ΔT的递增，Δa先会有一段平稳期 (此时误差在200m之内)，之后Δa会随之缓慢递增至一峰值，然后开始快速递减，当Δa减小至负值后，实际上定轨误差 (Δa的绝对值)是在快速递增。

显然，误差峰值及其对应的峰值时长是一对很有意义的量，且大小与轨道高度相关，现将二者分别记为和，其中h(单位默认为km)代表轨道高度。由上图可见:误差峰值及其对应的峰值时长均随轨道高度递增。

同时，考虑到定轨结果的实用性，当资料时长ΔT很大时，即使迭代计算可以收敛并给出定轨结果，仍有可能因为定轨误差太大而导致定轨结果无意义。为此引进有效时长的概念:

假定当Δa大于某阈值Da时定轨结果即视为无效，由于Δa随ΔT的增大而增大，当Δa达到阈值Da时对应的资料时长即称为有效时长，并用TD表示。本文中取Da=10 km。

表2 误差峰值及对应的资料时长Tab.2 Peak error and time length of corresponding data

以上结果均是由无资料误差 (严格来讲含有输出数据时带来的截断误差，其大小为1mm量级，在标准单位下是1.6×10-10)的数据计算得到，因此该定轨误差主要反映的是模型误差。对于峰值时长之后快速变化，显然与时间幂级数展开式F，G的变化规律一致:计算F，G时舍弃的余项随ΔT的增长以指数形式递增，由此带来的模型误差亦会快速增大。详细的误差演化规律仍有待进一步研究。

表2中有效时长与轨道高度的关系如图2所示，二者近似为线性关系，以此可作为选取定轨资料长度的简易判据。

图2 有效时长与轨道高度的关系Fig.2 The relationship between effective time length and orbital height

3.2 资料误差与理想时长的关系

在3.1节的分析中，所用定轨数据均未加入误差，但在实际的测量数据中随机误差是不可避免的。若在计算中对所选数据人为加入随机误差，对应的定轨结果必然会有不同。记资料误差σ引起的定轨误差为δaσ，a1、a2分别表示未加入、加入随机误差时半长径的定轨结果，则δaσ=a2-a1。图3是对300km高的轨道资料加入σ=20m的随机误差后，δaσ与ΔT的变化关系。

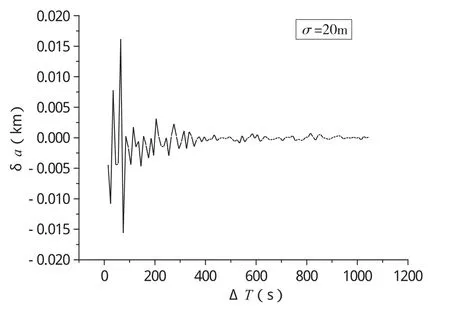
图3 资料误差引入的定轨误差与资料时长的关系Fig.3 The relationship between orbit determination error caused by data errors and time length of data

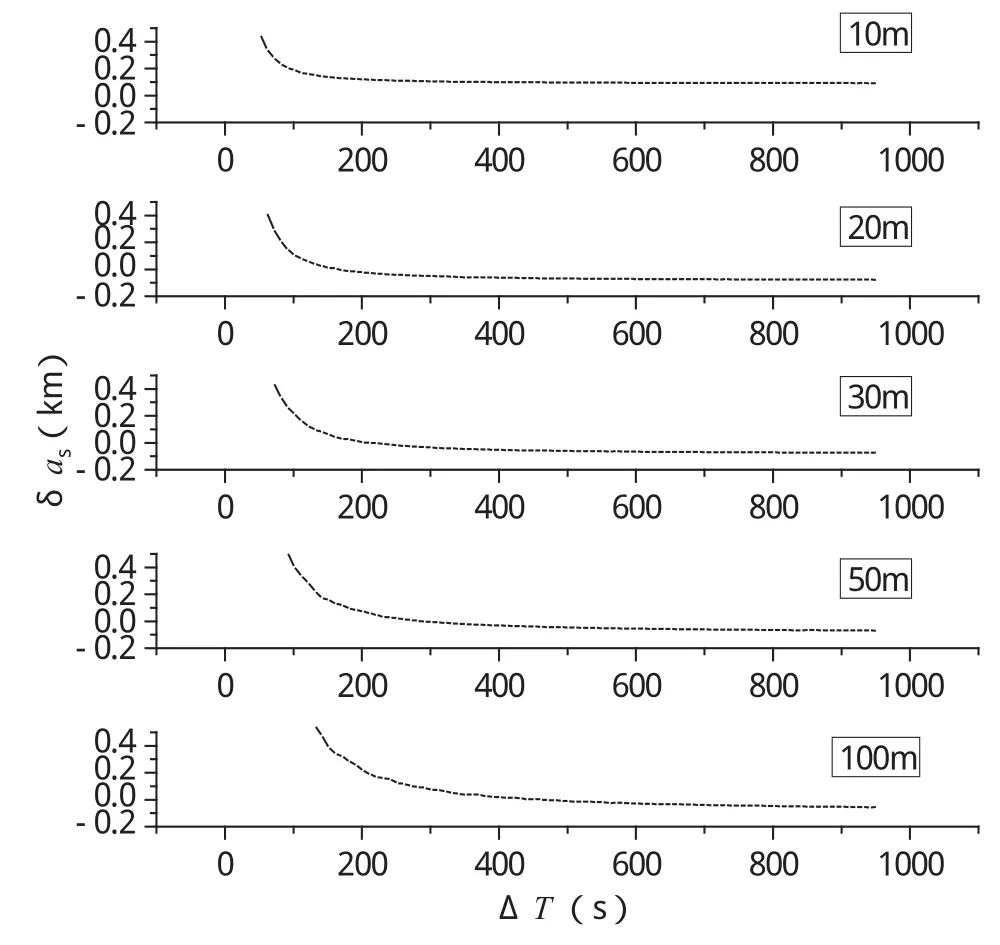
图4 300km高轨道δaσ随ΔT变化关系Fig.4 Variation of δaσ with ΔT for 300km high orbit

由于δaσ是渐变趋于零，故严格定义理想时长Tσ为:使得δaσ小于阈值δa的最小资料时长。

图5是取阈值δa=200m时对应的理想时长Tσ与资料误差大小σ的关系图，其中图a对应资料间隔为5s，σ的步长为5m；图b对应资料间隔为1s，σ的步长为2m的情况。定轨时刻均为所选弧段的中间时刻。可以看出Tσ与σ近似成线性关系，对轨道高度的变化并不敏感，只在σ较大时有缓慢的递增趋势；同时通过两图中Tσ大小的比较可以看出，Tσ与资料间隔密切相关。

3.3 定轨误差与资料密度的关系

定轨误差的大小与资料密度密切相关。此处以300km高的轨道为例分析定轨误差δaσ与资料密度的关系，其中资料密度用相邻数据的时间间隔表征。

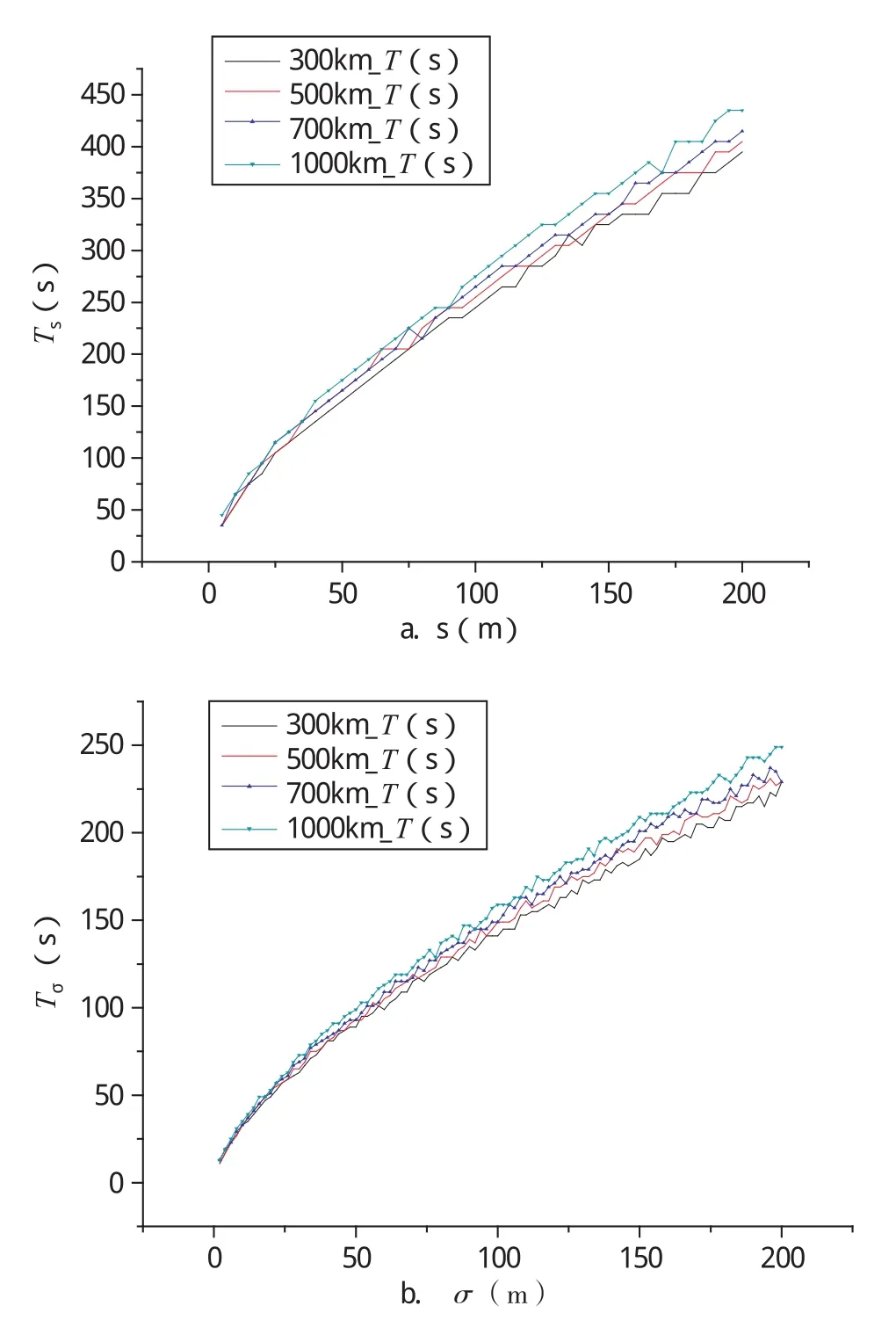
图5 理想时长Tσ与资料误差大小σ关系(a图：资料间隔为5s；b图：资料间隔为1s)Fig.5 The relationship between ideal time Tσand data error size σ.(a： data interval is 5s；b：data interval is 1s)

首先计算在不加入随机误差的情况下，采用不同时间间隔的资料进行初轨确定，对应的定轨误差与资料时长的关系如图6所示。

图6 无误差300km高轨道不同资料密度定轨误差图Fig.6 Orbital determination error map of different data densities for error-free 300km high orbit

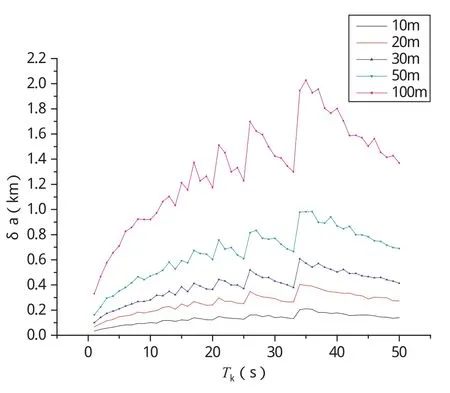
图7 100s资料定轨误差与时间间隔的关系Fig.7 The relationship between orbital determination error of 100s data and time intervals

图8 200s资料定轨误差与时间间隔的关系Fig.8 The relationship between orbital determination error of 200s data and time intervals

图9 400s资料定轨误差与时间间隔的关系Fig.9 The relationship between orbital determination error of 400s data and time intervals

由图10、11可见，在总体趋势上，δaσ随δT的增大而增大，因为所用资料个数在随之递减。对于图中跳变及递减的部分，实际反映的是在资料组数固定的情况下，定轨误差随资料间隔的增大在减小 (详见图10、11)。如图9中的最后一次跳变，对应的 δT为133s，之后直至 δT达到200s的区间之内，δaσ是随之递减的，分析可知，由于资料组数必为整数，在最大资料时长固定为400s时，δT在区间[134s，200s]内时均只有3组数据。同时，资料误差σ越大，定轨误差δaσ对资料密度越敏感。

图10、11依次是固定选用资料组数N为2组和5组，同时加入不同大小的随机误差时，定轨误差随时间间隔δT的变化关系图。其中纵轴为统计计算的定轨误差δaσ，计算方法同3.3中所述；横轴为相邻资料的时间间隔δT，由于选用资料组数已固定，因此δT越大对应的资料时长ΔT=NδT亦越大。计算时取δT的步长为2s，定轨历元 (记为Tm)同3.1，选取资料使得Tm恰为其中间时刻。

图10 2组资料定轨误差与资料间隔关系Fig.10 The relationship between orbit determination errors of 2 groups of data and data intervals

图11 5组资料定轨误差与资料间隔关系Fig.11 The relationship between orbit determination errors of 5 groups of data and data intervals

由图可见，在资料组数固定时，对于不同大小的随机误差，其定轨误差随时间间隔δT的变化趋势是一致的，均会有一拐点。记拐点处对应的时间间隔为δTσ，定轨误差为δaσ。在δT＜δTσ时，增大时间间隔可降低随机误差造成的定轨误差；δT＞δTσ时，情况恰好相反。同时亦可发现，在δT＞δTσ的部分，几条曲线很快便趋于一条，说明误差的影响不再是主导因素 (实际已转为模型误差为主导，正如3.1中表现出来的变化趋势)。以上两图中拐点对应的具体数据见表3:

表3 拐点处时长及误差列表Tab.3 Time length and error list at the turning point

4 结论与展望

本节主要讨论利用低轨近圆轨道的定位资料进行初轨确定的问题，分析了资料时长、资料密度以及资料误差的大小对定轨精度的影响，并根据定性的分析得到以下几点结论:

(1)初轨计算所用资料长度的选择，并非只要程序收敛即可，本文建议引入有效时长 (与其阈值相关)的概念，以此作为资料长度的上限；有效时长随轨道高度递增，在初步估计时可考虑采用线性近似的公式；

(2)资料随机误差引起的定轨误差会随资料时长ΔT的增加而迅速减小，在具有足够多观测资料的情况下，应选取资料使其长度大于理想时长 (与其阈值及与资料密度相关)以消除资料随机误差的影响；

(3)在资料时长ΔT固定时，所用资料组数越大定轨误差越小；在资料组数固定时，适当增大资料时间间隔δT可降低定轨误差。

对于初轨确定误差分析的工作，本文只对低轨近圆轨道的定位资料作了初步的分析，对于其余类型资料、其他各类轨道以及对应的理论分析仍有待进一步研究。