多目标遗传算法在波荡器垫补中的应用

闫陇刚，李 鹏，王建新，邓德荣，杨兴繁，黎 明

(中国工程物理研究院 应用电子学研究所，四川 绵阳 621900)

基于加速器的光源主要包括同步辐射和自由电子激光，这两类光源均通过波荡器中的周期性磁场产生强辐射光，因此其辐射性能很大程度上取决于波荡器的磁场和磁场误差[1-2]。目前最常用的永磁波荡器是由Halbach[3]于1980年代发明的，其包含两个以上由永磁块和软铁磁极组成的磁阵列。在永磁波荡器的制造过程中不可避免地会存在各种缺陷，如机械加工公差、磁铁或磁极的定位偏差、永磁块之间磁化强度与磁化方向的差异和单个永磁块磁化不均匀等，这均是波荡器磁场误差的来源[4-5]。波荡器磁场误差主要包括电子轨迹中心偏差、峰峰值误差、相位误差和高阶场等，若这些误差不能限制在一定范围内都会使光源性能下降[6]。波荡器磁场垫补通过对局部磁场进行小的修正来减小磁场误差，磁场垫补方法分为两类：移动磁铁或磁极方位的机械垫补和在永磁块或磁极表面贴软磁片的磁垫补，这两类方法中局部垫补量的精确推算是关键步骤之一[7]。目前，在特定某一局部位置，机械垫补位移量和磁垫补软磁片尺寸已能用解析方法计算[8-9]，针对特定的误差指标，全局各点的垫补量也能通过解析方法或优化算法进行推算[10-12]。但波荡器磁场误差指标一般有多个，且很多情况下相互冲突，由于现有垫补量推算方法的限制，只能分别针对每个误差指标依次进行垫补，然后再对磁场进行复测，若有磁场误差不满足指标要求，还必须再次对磁场进行调整，这使得磁场垫补工作效率十分低下[13]。因此，发展基于多目标优化算法的磁场垫补量推算方法十分迫切，将有可能通过1次垫补使得波荡器磁场误差满足所有指标要求。

遗传算法是一种通过模拟自然进化过程搜索最优解的方法，其主要优点包括：具有良好的全局寻优能力，且搜索过程不易陷入局部最优解；不需确定规则，却能自动获取和调整搜索方向；无求导和函数连续性的限定；具有固有的并行性；可扩展性强[14]。遗传算法最早由Holland[15]于1975年进行了系统论述，目前已发展出多个变种，广泛应用于各领域，尤其在组合优化问题中显示出更多优势[16]。

中国工程物理研究院太赫兹自由电子激光(CTFEL)装置是国内首台工作在太赫兹波段且具有高重复频率和高占空比的谐振腔型自由电子激光器，该装置目前已饱和出光，并为国内外用户提供实验机时[17-18]。为对CTFEL装置的辐射性能进行扩展，计划在CTFEL装置束线直线段后建立1套超辐射源，并借鉴中国科学院上海应用物理研究所波荡器U38研制1台波荡器U38-S。本文将多目标遗传算法应用于波荡器U38-S磁场垫补量的推算，为减小电子轨迹偏移、相位误差和峰峰值误差，对波荡器U38-S的磁场进行垫补。

1 U38-S指标要求

U38-S指标要求列于表1。U38-S波荡器具有典型的Halbach型磁结构[19]，磁结构上下两排磁阵列各有12个标准周期，间隙固定在18 mm。U38-S需要优化的误差指标包括轨迹中心偏差、相位误差和峰峰值误差，需分别小于0.2 mm、5°和0.5%。

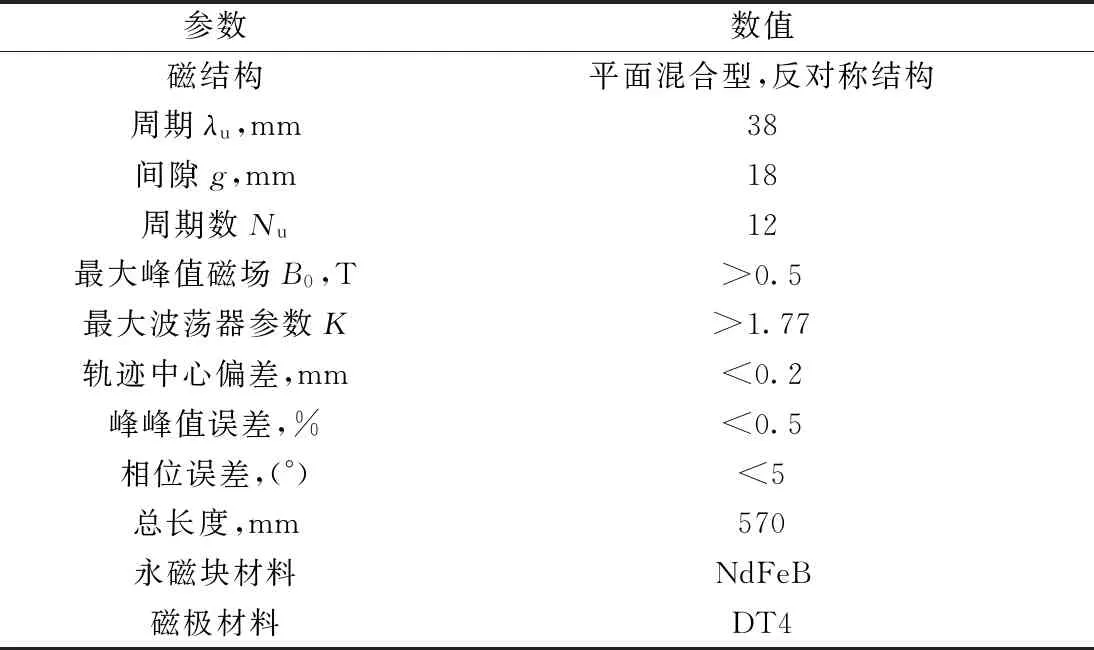
表1 U38-S指标要求Table 1 Specification requirement of U38-S

2 多目标遗传算法

遗传算法中优化问题的候选解称为个体，个体拥有1个或多个染色体，若干个体组成1个种群，种群经过类似自然进化的过程最终得到最优个体。典型遗传算法的基本流程如下：

1) 初始化，随机或以一定方式产生初始种群的个体；

2) 终止判断，判断种群是否达到终止要求，若是则停止进化，若不是则进入下一步进化；

3) 个体评价，计算种群中个体的适应度，作为后续选择的依据；

4) 选择，依据种群中个体的适应度，选择适应度高的个体直接遗传到下1代或通过交叉变异产生新的个体再遗传到下1代；

5) 交叉，群体中个体随机配对，并按随机确定的交叉点交换一定数量的基因；

6) 变异，改变种群中个体的染色体随机位置的基因；

7) 新种群产生，群体经过选择、交叉、变异后产生下1代种群，新种群进入步骤2进行判断。

实际工程优化一般有多个目标，且大多数情况下目标之间是相互冲突的，在多目标遗传算法中有权重系数变换法、并列选择法、排列选择法、共享函数法和混合法等来处理这个问题[20]。其中权重系数变换法最为简便常用，其给第j个子目标函数tj(p1,p2,…,pl)赋予权重系数wj，全部k个子目标函数线性加权组成新的目标函数T(式(1))，通过这种方法将多目标优化问题转化为单目标优化问题。

(1)

3 计算模型

3.1 垫补量推算问题的规范化

U38-S的磁结构和1/2周期单元如图1所示。1/2周期单元是磁结构的标准组件，其具有两个半磁块夹1个磁极的三明治结构，这种磁结构既便于加工和安装，又易于磁场垫补。磁场垫补时可在1/2周期单元与底板之间塞入一定厚度的铜片，通过改变1/2周期单元的位置来改变局域磁场。

图1 U38-S的磁结构和1/2周期单元Fig.1 Magnetic structure and 1/2-period unit of U38-S

为明确1/2周期单元位移量d与其产生的局域磁场变化之间的关系，分别在Radia[21]和OPERA中建立了U38-S磁结构的物理模型并进行了计算。图2为1/2周期单元移动0.001 mm后附近5个1/2周期单元范围内的局域磁场变化，该曲线用S(z′)来表示，其中-5/4λu

(2)

图2 1/2周期单元移动0.001 mm后5个1/2周期单元内的局域磁场变化Fig.2 Modification of local magnetic field in range of five 1/2-period units after displacing of 0.001 mm for 1/2-period unit

3.2 多目标函数

1) 轨迹中心偏差

B(z)下的电子轨迹x(z)为：

(3)

其中，γ、c、m0和e分别为电子相对论因子、光速、电子静止质量和电子电荷。

Δxn_center=(xn+xn+1)/2

(4)

其中，xn和xn+1分别为相邻最大和最小两个轨迹峰值。轨迹中心偏差Δxrms定义为2Nu个Δxn_center的均方根差。

2) 相位误差

B(z)下的相位Φ(z)为：

(5)

第i个磁极处的相位误差ΔΦ(zi)等于磁极处相位减去2iπ：

ΔΦ(zi)=Φ(zi)-2iπ

(6)

则相位误差(ΔΦ)rms定义为2Nu个ΔΦ(zi)的均方根值。

3) 峰峰值误差

峰峰值误差(ΔB/B)rms也是所有峰值磁场绝对值的均方根差。

U38-S需优化的误差指标包括轨迹中心偏差、相位误差和峰峰值误差，因此多目标函数应是它们的线性叠加。希望以上3个指标在优化过程中应具有相等的地位，但它们的数值大小不在同一范围内，因此通过权重系数将它们变换到大致相当的范围内，于是多目标函数T(B(z))为：

T(B(z))=10Δxrms+

(ΔΦ)rms+500(ΔB/B)rms

(7)

U38-S指标要求只有3个目标量，对于其他指标要求更多的波荡器如椭圆极化波荡器，以上方法同样适用，仍是以合适的权重系数对所有目标量进行线性叠加得到目标函数。另外，U38-S指标要求的3个目标量的优先级是平级关系，在其他波荡器中若出现某个目标量相对拥有一定优先级，可通过适当增加该目标量的权重系数来实现。

3.3 算法配置

遗传算法优化结果与效率对参数和配置较敏感，根据以往经验确定遗传算法参数(表2)。另外，算法配置还有以下特点。

1) 编码。合理的编码能大幅提高遗传算法效率，一般会将实数转换为二进制。这里将Cn转换为六位二进制码，共有2Nu个Cn，则每个个体染色体均为6×2Nu的二维矩阵，其组成形式如图3所示。

2) 初始化。遗传算法一般采用随机方法产生初始种群，但波荡器磁场垫补不同，其每个1/2周期单元的初始位移量均为0，因此将初始种群个体的Cn均置为0，同时这也在一定程度上限制了需垫补的1/2周期单元数。

3) 精英选择。为加快进化速度和保证在进化过程中最优解不会丢失，在个体选择时保留一适应度最高的个体直接进入下1代，而不经过交叉和变异过程。只保留1个的原因是若保留的精英数过多，易陷入局部最优解。

表2 遗传算法参数Table 2 Parameter of genetic algorithm

图3 个体染色体编码结构Fig.3 Structure of individual’s chromosome

4 U38-S磁场垫补

基于上述计算模型，使用Python语言编写了计算程序，并调用了Pyevolve遗传算法库[23]。Pyevolve定义了1组染色体类型、交叉变异算子和选择方法等，用户可按照需要进行调用，从而将主要精力放在算法本身上。本文染色体表达类型是二维二进制字符串G2DBinaryString，交叉算子是水平单点交叉法G2DBinaryStringXSingleHPoint，变异算子是随机翻转法G2DBinaryStringMutatorFlip，选择方法是锦标赛选择GTournamentSelector。

利用磁场点测台测量了U38-S中心轴线上的磁场，磁场点测台的工作模式为go-stop，测量步长为0.5 mm，停顿时间为0.5 s，高斯计测磁精度和分辨率分别为0.05%和0.1 Gs。基于磁场点测台的测量结果，利用计算程序计算了所需垫补量，并对U38-S进行了3次垫补，图4a为每次垫补的1/2周期单元位移量，图4b为电子轨迹及轨迹中心的进化过程。图5为相位误差和峰峰值误差的进化过程。每次磁场垫补后磁场指标均有所提高，且需垫补的1/2周期个数也逐渐减少。第3次垫补后，轨迹中心偏差、相位误差和峰峰值误差分别减小到0.15 mm、1°和0.49%，满足了U38-S的指标要求。理想情况下在引入多目标遗传算法推算磁场垫补量后，只需1次垫补就可达到所有指标要求，但本文进行了3次垫补，主要原因可能是垫补机械结构精度不够，导致位移量不能精确控制。

图4 1/2周期单元位移量(a)与电子轨迹及轨迹中心的进化过程(b)Fig.4 Displacement of 1/2-peroid unit (a) and evolution of electron trajectory and trajectory center (b)

图5 相位误差(a)和峰峰值误差(b)的进化过程Fig.5 Evolution of phase error (a) and peak-to-peak error (b)

5 结论

本文将多目标遗传算法应用于垫补量的推算，对波荡器U38-S的磁场进行了垫补，经过3次磁场垫补U38-S的性能达到指标要求，轨迹中心偏差、相位误差和峰峰值误差分别减小到0.15 mm、1°和0.49%。相比其他方法，多目标遗传算法在垫补量推算上具有一定优越性，可同时针对多个指标进行磁场垫补，且由于遗传算法具有很好的可扩展性，因此对于其他类型的波荡器磁场垫补也会有很好的适用性。