高能同步辐射光源中的耦合阻抗及束流集体效应研究

王 娜，许海生，田赛克，段 哲，李啸宇

(中国科学院 高能物理研究所 粒子加速物理与技术重点实验室，北京 100049)

同步辐射光源作为一种具有波长覆盖范围广、亮度高等特点的高性能、多用户装置，为物理、化学、生命科学、医学、材料等诸多领域的发展起到了重要的支撑作用，是一种解决重大科学问题的多学科平台。而高能量的同步辐射光源从性能上讲，属于同步辐射光源中的旗舰装置。目前世界上已有3台高能量同步辐射光源在运行，分别是欧洲的ESRF(6 GeV)[1]、美国的APS(7 GeV)[2]和日本的SPring-8(8 GeV)[3]。这3台光源均提出了基于具有极低发射度的(准)衍射极限电子储存环的升级计划，其中，ESRF的升级项目ESRF-EBS[4]和APS的升级项目APS-U[5]已在进行中。为服务国家重大需求，中国科学院高能物理研究所正设计一台基于具有极低发射度(几十pm)的(准)衍射极限电子储存环的高能同步辐射光源(HEPS)[6]。

这种具有极低发射度的(准)衍射极限储存环需要更强的四、六极磁铁来实现更低的发射度，因此需尽可能小的真空盒孔径，这就导致了全环耦合阻抗的增加。除此之外，这种(准)衍射极限储存环的动量压缩因子显著小于第3代同步辐射光源，因此束流更易受到束流集体效应的影响。(准)衍射极限储存环中的束流集体效应可能成为限制机器性能的重要因素，需系统地评估束流集体效应对HEPS电子储存环束流参数的影响。本文基于解析理论和数值模拟程序对HEPS储存环耦合阻抗进行逐元件建模，并对环中可能发生的束流集体效应进行系统评估。建立合理的阻抗模型，给出不稳定性阈值和增长时间，并对关键的不稳定性问题提出有效的抑制措施。

1 HEPS储存环磁聚焦结构

经过不断的优化迭代，HEPS储存环的发射度达到34 pm，本文的阻抗及束流集体效应计算基于该方案的基本参数(表1)，并考虑了HEPS一期的插入件参数的影响。

2 阻抗计算

束流阻抗主要源于环中的非理想导体真空盒及非光滑或非连续结构引起的束流电磁场的变化。基于HEPS储存环磁聚焦结构和真空系统设计，对关键真空元件进行了逐元件建模。阻抗模型包括电阻壁、高频腔、谐波腔、波纹管、法兰、真空盒过渡段、真空内插入件、注入及引出冲击磁铁、横向及纵向反馈kicker、束流位置探测器及真空泵口等。阻抗计算中，电阻壁阻抗采用理论公式[7]，几何结构阻抗采用ABCI[8]和CST[9]程序进行数值模拟计算。图1为纵向和横向阻抗的计算结果。

表1 HEPS储存环磁聚焦结构主要参数Table 1 Main parameter of lattice of HEPS storage ring

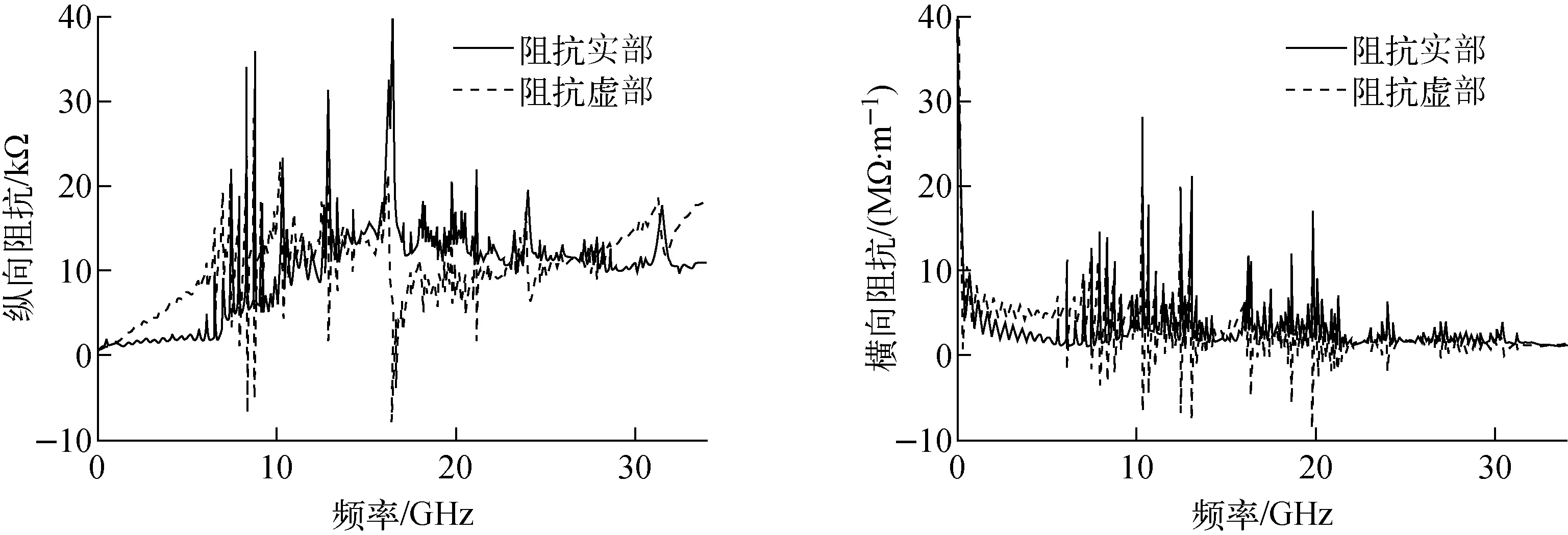
图1 纵向和横向阻抗的计算结果Fig.1 Calculation result of longitudinal and transverse impedances

3 束流集体效应

束流集体效应的来源主要包括束流阻抗、残余气体离子和束内散射(IBS)等。对于高能同步辐射光源而言，单束团流强通常受限于横向宽带阻抗；而纵向宽带阻抗通常引起束长拉伸、能散度增长和寄生功率损耗，会在一定程度上影响同步光的性能，不会直接引起束流损失。同时，储存环中类腔结构会引入横向和纵向的窄带阻抗，从而可能引起耦合束团不稳定性。此外，横向发射度的降低导致电子密度增加，离子效应和束内散射可能导致束流发射度的增长，从而影响同步光性能。

综上所述，在设计阶段需对束流集体效应给出准确、系统的评价。并根据研究结果，对可能发生的不稳定性机制提出合理的抑制手段，同时基于束流稳定性要求对各种真空元件提出阻抗优化要求和建议，从而保证光源在高流强情况下稳定运行，实现预期的机器性能。

3.1 微波不稳定性

微波不稳定性是一种重要的纵向单束团不稳定性。在HEPS储存环中，采用基频腔与三次谐波腔配合的方法提供束长拉伸，这将有利于抑制微波不稳定性。使用Elegant程序[10]及其并行版本Pelegant[11]进行微波不稳定性的模拟计算。为验证使用谐波腔对微波不稳定性的抑制效果，分别计算了有、无谐波腔两种情况下束团的束长及能散随单束团电荷量的变化，结果如图2所示。

由图2可看出，设置三次谐波腔后，在零流强下束长有接近5倍的拉伸，并且随单束团电荷量的增加，束长拉伸的比例相对于无谐波腔的情况有所降低；此外，使用谐波腔后微波不稳定性的阈值显著提高，且在阈值以上束团能散明显降低，进一步验证了谐波腔对于微波不稳定性的抑制作用。

在设计流强(单束团电荷量约为1.3 nC)下，有、无谐波腔两种条件下束团在纵向相空间(z，δ)中的分布如图3所示。可看出，不使用谐波腔时，束团受到微波不稳定性的影响在纵向相空间产生复杂的微结构，同时伴随能散的增加；使用谐波腔拉伸束长后，束团在纵向相空间中的微结构消失，且未见明显能散增长。

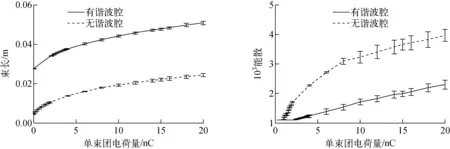
图2 束长和能散随单束团电荷量的变化Fig.2 Variation of bunch length and energy spread with single bunch charge

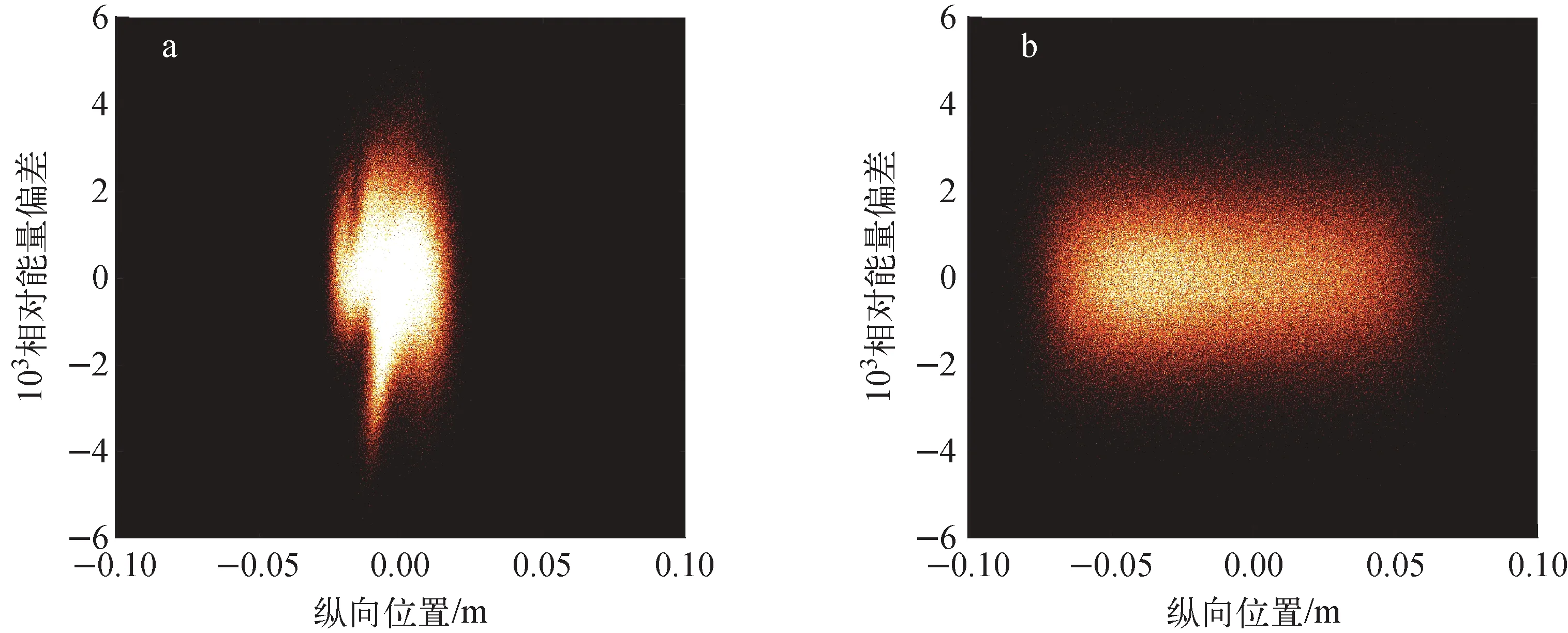
图3 有(a)、无(b)谐波腔两种条件下束团在纵向相空间中的分布Fig.3 Bunch distribution in longitudinal phase space with (a) and without (b) harmonic cavity

3.2 横向单束团不稳定性

横向单束团不稳定性会导致束团横向发射度的快速增长甚至产生粒子丢失，因此，横向单束团不稳定性通常是单束团电荷量的重要限制因素。本文分别利用本征模分析方法和多粒子跟踪模拟对横向单束团不稳定性进行计算。通过对横向头尾模式的分析，可获得横向单束团不稳定性的阈值如图4所示。图4a为本征模分析得到的头尾模式随单束团流强的变化，可看出，当单束团流强达到0.05 mA时，0和-1两个模式发生耦合，即发生头尾不稳定性；图4b为模拟结果，图中颜色对应束团质心振荡的傅里叶变换频谱的幅度，可看出，当单束团流强达到约0.053 mA时，0和-1两个模式发生耦合，与本征模计算结果符合较好。

以上是考虑零色品的情况。根据经验，非零色品可进一步提高横向单束团不稳定性阈值，此外，谐波腔的引入同样会对横向单束团不稳定性产生影响。同时考虑以上两个因素，在+5色品情况下，利用多粒子模拟得到不同电荷量下束团质心振荡和发射度随圈数的变化(图5)。结果表明，当单束团电荷量达到40 nC时，束团质心在y方向最大振荡幅度显著增大，但并未发现粒子丢失。考虑到模拟中未加入误差、振动、精确的真空管道尺寸等因素，可保守地估计横向单束团不稳定性限制的最大电荷量在30～40 nC之间，远高于HEPS储存环设计所需单束团的电荷量。因此，将色品校正到+5可避免HEPS储存环受到横向单束团不稳定性的限制。

3.3 耦合束团不稳定性

横向耦合束团不稳定性的主要来源包括横向电阻壁阻抗和高频腔的高次模。电阻壁不稳定性主要源于横向电阻壁阻抗在零频率附近的共振峰。通过理论计算得到横向电阻壁阻抗导致的耦合束团不稳定性增长时间约为0.44 ms。为抑制该不稳定性，需横向逐束团反馈系统提供阻尼。此外，正色品的引入也有利于抑制该不稳定性。针对高频腔高次模引起的耦合束团不稳定性，本文采用保守估计，即假定高次模的谐振频率与束流谱线重合，横向和纵向阻抗阈值可表示为[12]：

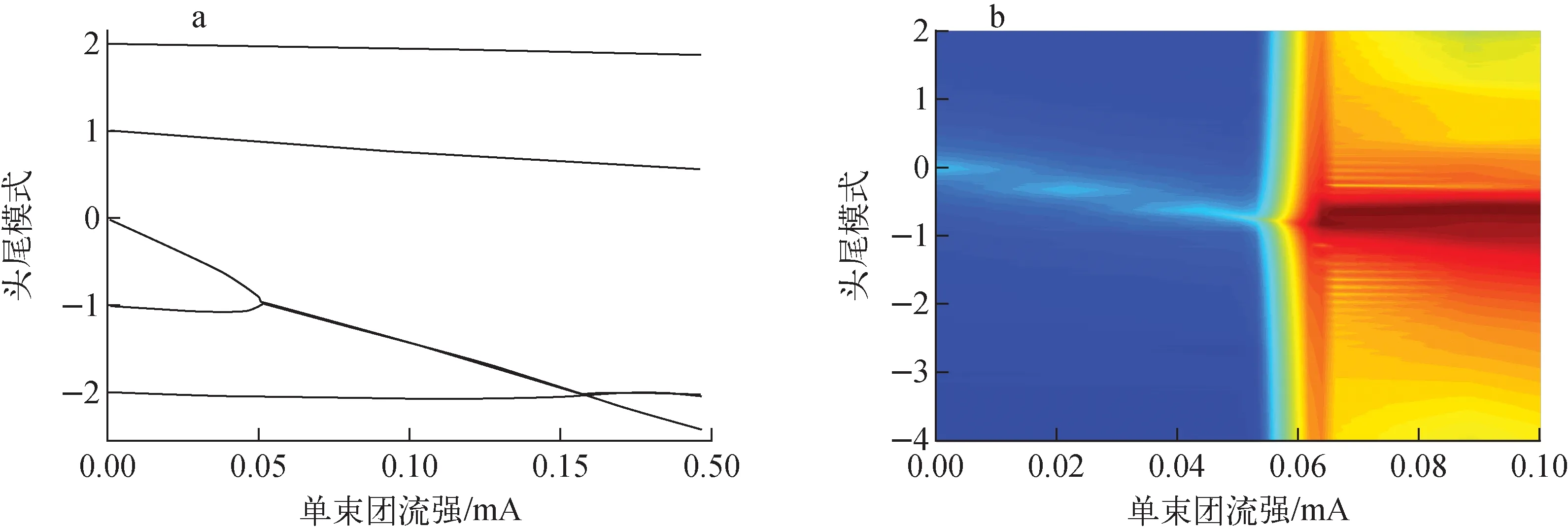
图4 横向单束团不稳定性的阈值Fig.4 Threshold of transverse single bunch instability

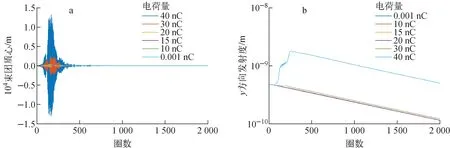
图5 不同电荷量下束团质心振荡(a)和发射度(b)随圈数的变化Fig.5 Variation of bunch centroid oscillation (a) and emittance (b) with number of turn at different charges

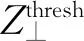
不考虑三次谐波腔和反馈系统的情况下，横向和纵向阻尼由同步辐射阻尼主导，计算得到横向高次模阻抗阈值约为1.5 MΩ/m，纵向高次模阻抗阈值随高次模谐振频率的变化如图6所示。考虑三次谐波腔的情况相对复杂，本文利用Bosch[13]提出的方法计算纵向阻抗阈值(图6)。

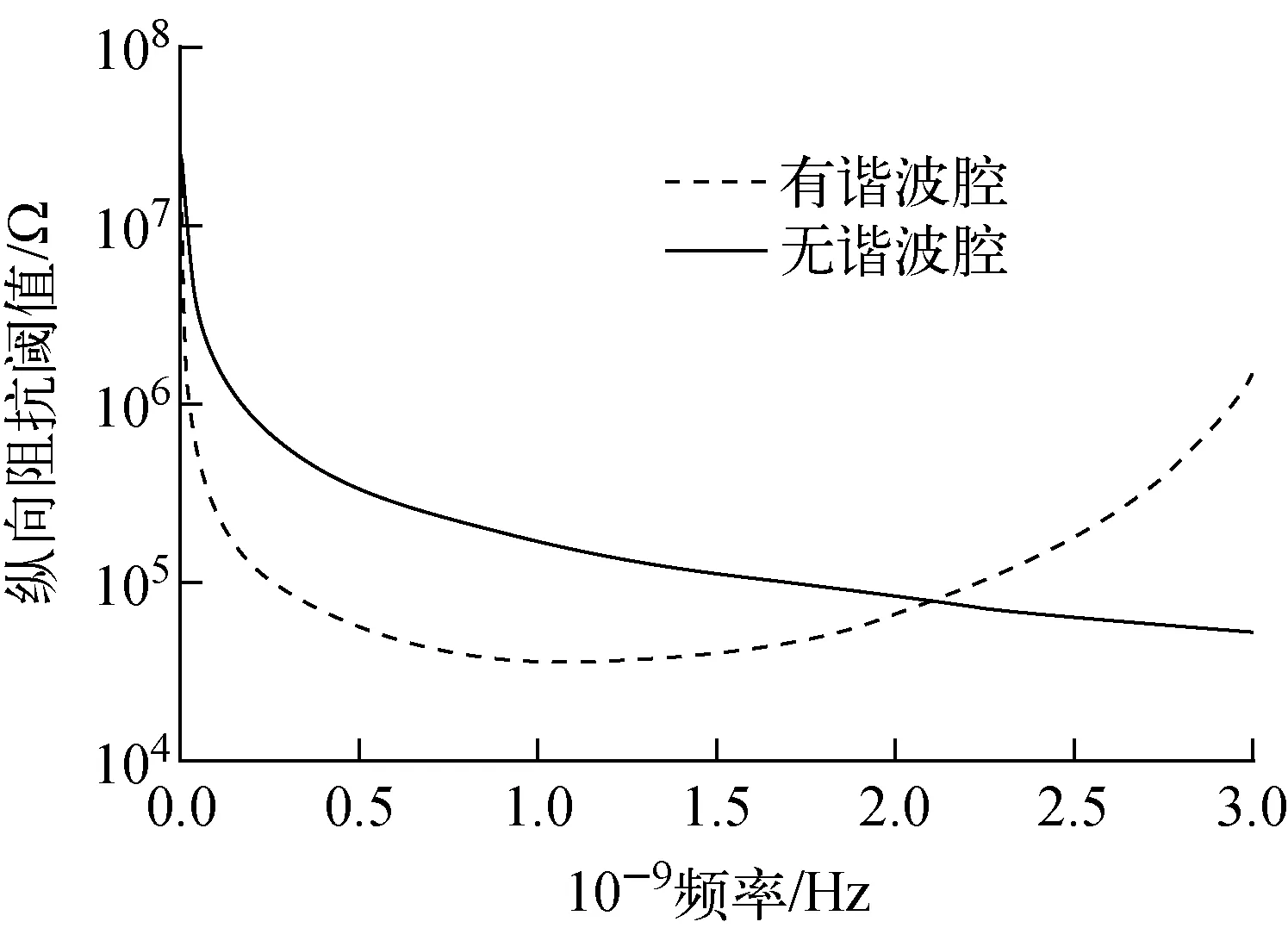
图6 纵向阻抗阈值随高次模谐振频率的变化Fig.6 Threshold of longitudinal impedance vs high order mode resonant frequency

3.4 离子效应

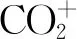
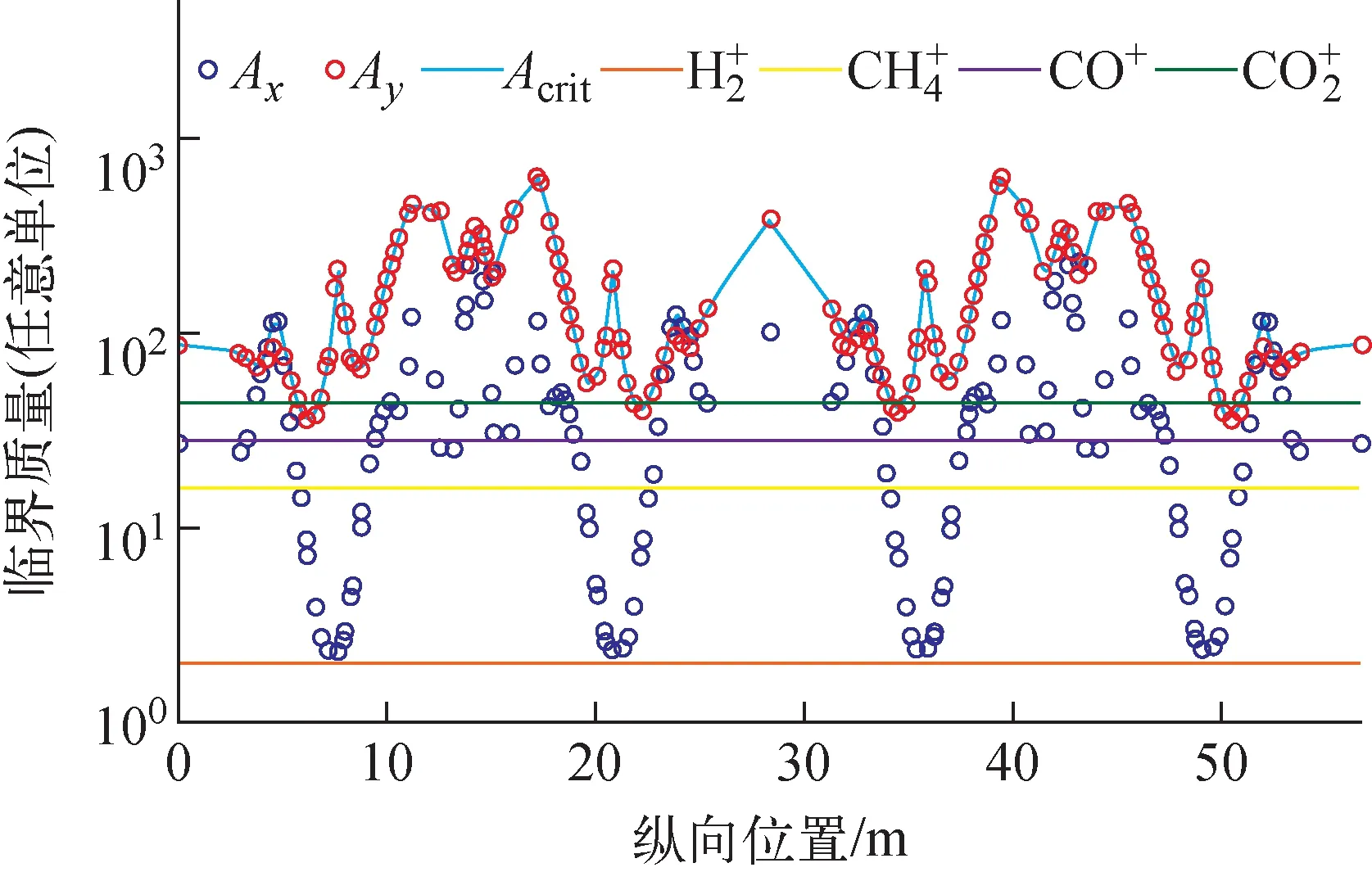
图7 发生离子俘获的临界质量在1个lattice周期内的分布Fig.7 Critical mass of ion trapping along one lattice period

尽管引入束团串间隙可避开离子俘获效应，但在单个束团串内部仍可能发生快离子不稳定性。利用强弱模型理论[15]对快离子不稳定性增长时间进行了数值模拟评估。计算得到快离子不稳定性增长时间约为4 ms，该增长时间远小于同步辐射阻尼时间，需利用横向反馈系统进行抑制。

3.5 束内散射效应

HEPS储存环自然发射度很小，IBS造成的束团六维相空间发射度的增长将不能忽略。利用Elegant程序基于Bjorken-Mtwingwa模型[16]分别计算了200 mA流强下束流平衡态参数，在未考虑谐波腔的情况下IBS将导致明显的发射度增长和能散增长(图8)。进一步研究表明，当引入谐波腔后，IBS被显著抑制。

4 结论

本文基于HEPS储存环的物理和真空元件设计，对全环主要阻抗元件进行了逐一建模，得到了全环阻抗模型。基于该阻抗模型，对可能发生的束流集体效应进行了研究，其中横向单束团不稳定性限制了可能达到的单束团流强，需引入正的色品对该不稳定性进行抑制，以满足设计流强的要求；而纵向单束团不稳定性不会成为流强提高的限制因素，但会在一定程度上影响同步光性能。另外，通过对耦合束团不稳定性和离子效应的研究，发现不稳定性增长时间远小于同步辐射阻尼时间，因此需引入反馈系统对其进行抑制。此外，计算得到了束内散射效应对束流平衡态参数的影响。

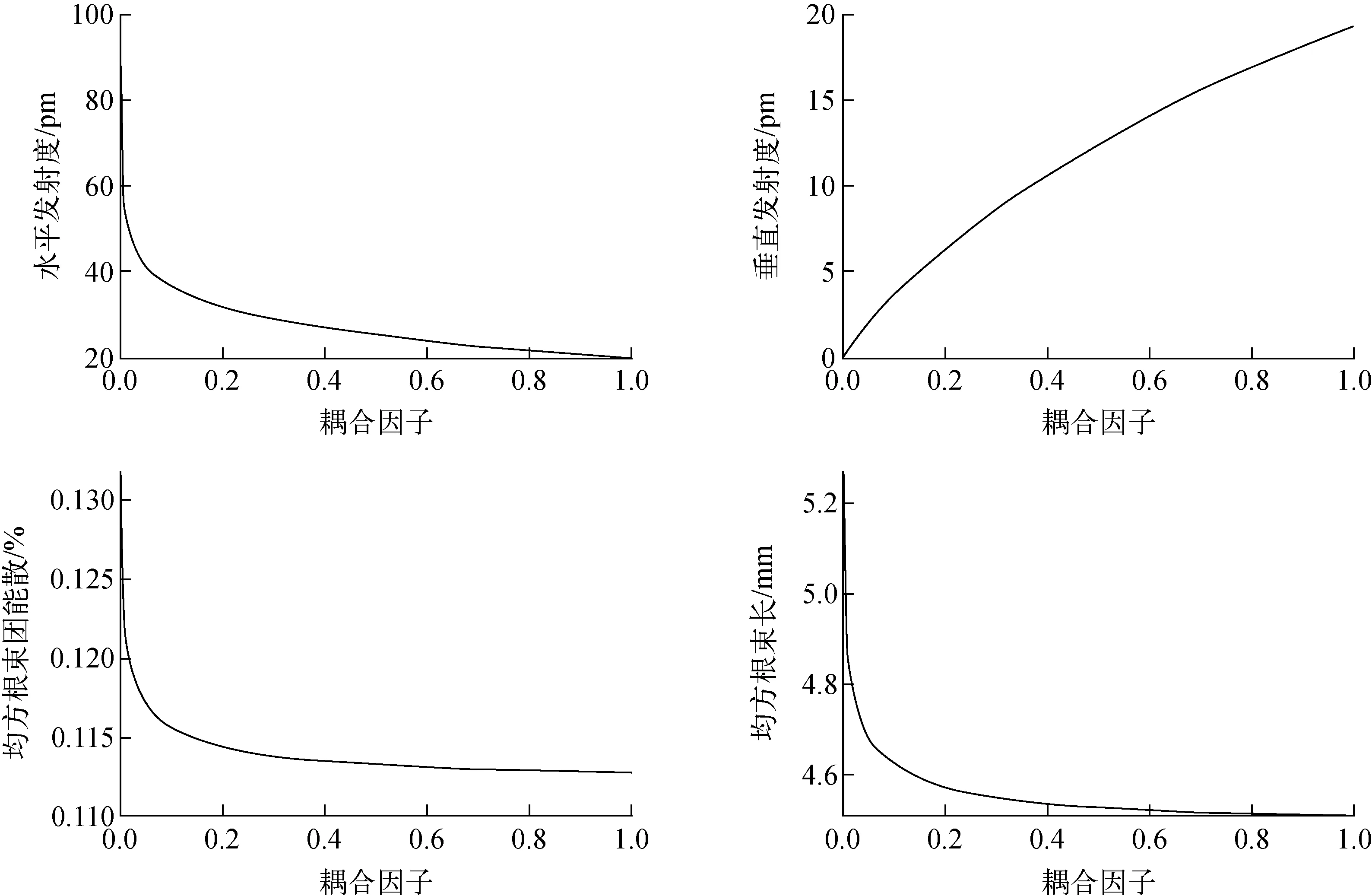
图8 200 mA流强下IBS导致束流参数随发射度耦合因子的变化Fig.8 IBS induced variation of beam parameter with coupling factor at beam current of 200 mA