电子回旋自共振加速器输出能量的影响因素及优化

袁雅婷，樊宽军，江 涌

(1.华中科技大学 强电磁工程与新技术国家重点实验室，湖北 武汉 430074；2.耶鲁大学，纽黑文 06520，美国)

Kolomenskii等[1-2]于1962年首次提出了自共振现象：在沿着静态均匀磁场传播的横向电磁波中，相对论性带电粒子有可能保持自共振状态一直被加速。带电粒子在轴向静态磁场的作用下做回旋运动，因此也称为回旋自共振加速。回旋自共振加速机制一般应用于电子加速，在离子与质子加速上也有应用[3-7]。

在回旋自共振加速过程中，随电子能量和速度的增加，轴向磁场或波导半径需逐渐改变以维持电子回旋频率与旋转的TE11模微波场保持相位同步，达到自共振状态[8]。在同步情况下，电子沿螺旋轨迹向前，在不需要聚束的条件下可获得连续加速。因此回旋自共振加速器(CARA)能以高达96%的效率将微波场能量传递给电子束[9-11]，且输出电子束流强大、功率高。此外，CARA中的加速腔体为单腔波导，不需要多个加速腔体的级联，结构简单。这些特点使CARA适用于大功率的工业电子辐照应用，如烟气、废水等辐照处理[11-13]，并有潜力作为下一代电子源[13]。本文对影响CARA输出电子能量的因素进行分析研究。

1 理论分析

在CARA中，旋转的TE11模微波场对电子束进行横向加速，在渐变轴向磁场B0(z)的约束下，电子沿螺旋轨迹向前加速运动。当轴向静态磁场满足一定条件时，旋转的电子将被旋转的TE11模横向电场持续加速。电子回旋频率Ω(考虑到相对论因子γ)为：

Ω=eB0(z)/m0γ

(1)

其中，e、m0分别为电子电荷量及静止质量。

当电子感受到的TE11模微波场频率(考虑多普勒频移)等于电子的回旋频率时，电子将与横向电场达到同步状态：

ω-kzcβz-Ω=0或b0=γ(1-nβz)

(2)

其中：ω=2πf为微波场角频率，f为微波场频率；kz为z方向的波数；c为光速；βz为电子在z方向的归一化速度；n为折射系数，n=kzc/ω；b0为归一化的电子回旋频率，b0=eB0(z)/m0ω。

由同步状态下的式(2)可进一步得到轴向静态磁场的表达式：

(3)

电子做回旋运动的频率为：

(4)

根据回旋自共振加速原理可知，在CARA中，选择合适的轴向静态磁场，保持电子与横向电场的同步是使电子持续加速的关键。根据式(3)，磁场与折射系数、电子能量及电子轴向速度分量相互影响。此外，电子的状态又受到微波场、电子注入能量等因素影响。因此采用迭代优化方法对轴向背景磁场进行优化，保证电子束被持续加速。

在加速过程中，受横向电场的作用，电子束横向速度不断增大。横向速度与微波场的横向磁场作用产生z方向的洛伦兹力，该洛伦兹力不做功，但是将电子的横向速度转移到轴向速度，因此电子的轴向速度也有所增加。轴向静态磁场为满足共振条件需沿轴向逐渐增大，由于磁镜效应，电子束在加速到阈值后将会无法穿越渐强的磁场而停止前行，并开始返回入射端。此阈值为电子束在CARA中的理论能量上限，用相对论因子γmax[10]表示，经过一定的简化，可近似为：

(5)

其中：n1为出口处的折射系数；γ0为电子注入时的相对论因子。

相应表示成电子能量为：

Wmax=0.511(γmax-1)

(6)

其中，Wmax为相对论因子γmax对应的最大能量。

式(5)表明电子束在CARA中的理论能量上限仅与相对论因子γ0及折射系数n1有关。电子注入能量越高，折射系数n1越接近于1，能量上限越高。但实际上，理论能量上限还受微波场强、波导长度、轴向磁场等因素的影响。

2 仿真分析

电子在CARA中的理论能量上限受多种相互关联的因素影响，难以给出清晰的解析表达。利用数值仿真，优化电子注入能量、TE11模微波场强、波导长度等参数。基于此，得到一个多因素的优化组合，使得电子束输出能量最大。

微波场强即为腔体中建立起的微波电场和磁场的场强，微波场强越强，电场和磁场场强也越强。由于加速场为电场，因此用电场峰值场强Epeak来表征微波场强。CARA的注入电子由常规的电子枪引出，其能量在10～500 keV之间[14]。CARA的输出电子能量为2～4 MeV[15]，用于工业辐照。由于CARA目标输出能量不高，电子的注入能量在10～200 keV之间，TE11模微波场的电场峰值场强为1～20 MV/m，以保证加速器运行的稳定和安全。波导长度没有较为严格的取值范围，要求给电子提供足够的加速长度使其输出能量达到目标，但同时也希望波导长度不太长。

利用三维电磁场仿真软件CST建模并进行粒子跟踪仿真，自编程序进行轴向静态磁场迭代优化及粒子跟踪。波导腔为均匀圆柱形波导，其尺寸及CARA的相关参数列于表1。

表1 CARA的相关参数Table 1 Related parameter in CARA

2.1 注入能量对输出电子束参数的影响

固定微波场强(Epeak=5 MV/m)及波导长度(l=1.062 m)，在不同的电子注入能量W0下优化同步磁场。相应可得到准同步状态下电子束输出能量W1、能量增益ΔW、初始轴向磁场B0、回旋圈数、渡越时间t、轴向速度增益Δvz、横向速度增益ΔvT及γmax。注入能量对输出电子束参数的影响列于表2。

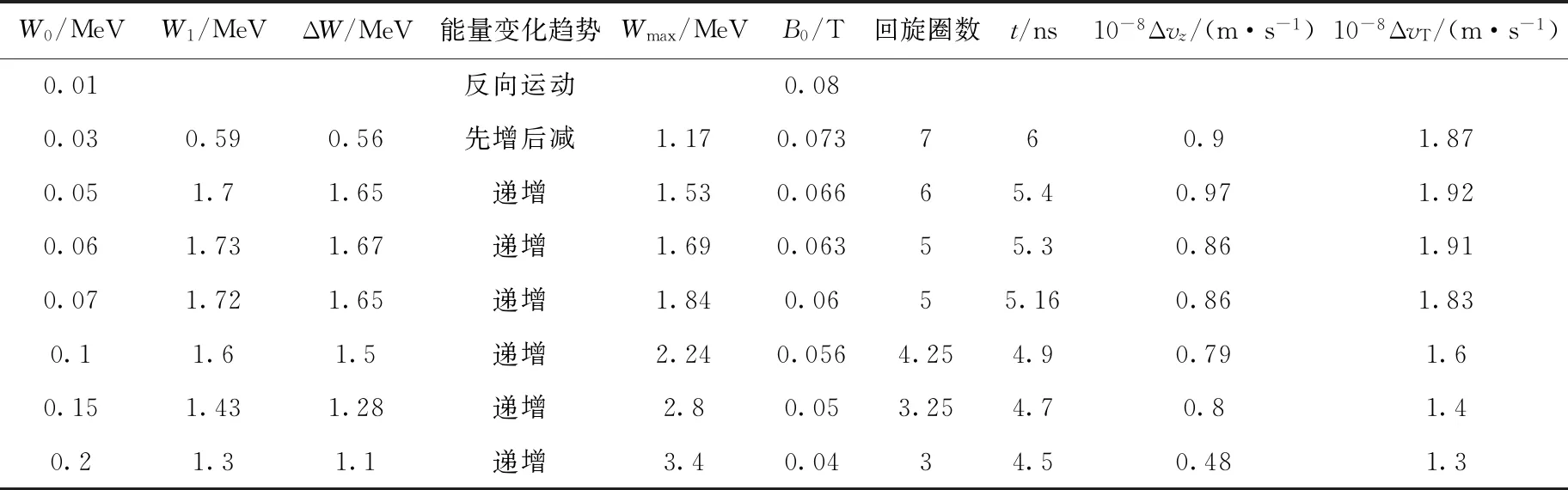
表2 注入能量对输出电子束参数的影响Table 2 Effect of injection energy on output parameter of electron beam

由表2知，Wmax随电子注入能量递增。但输出电子的能量增量ΔW先增大后减小，表明加速效率在减小。初始轴向磁场B0、回旋圈数、渡越时间、横向及轴向速度增益等参数随电子注入能量的增加而减小。

由于磁镜原理，当电子穿越渐强的磁场时，轴向静态磁场Bz的径向分量Br会给电子带来轴向减速力。因此电子注入能量W0越小，初始轴向速度vz越小，电子越容易反向，此时应适量减小微波场强。当电子注入能量W0较小时，由于微波场强较强、波导长度较长，导致电子束与微波场失谐，电子能量先增后减，此时应适量减小微波场强或减短波导长度。当电子束注入能量与微波场强、波导长度较为匹配(W0=0.05 MeV)时，电子在加速过程中能量一直增大，且输出能量与理论能量上限相符。当W0持续增大时，ΔW反而减小。因为W0越大，渡越时间越短，电子受加速电场力作用的时间越短。虽然增大W0能增大Wmax，但受加速梯度及渡越时间的限制，在微波场强及波导长度不变的情况下，电子输出能量W1并不随W0增加。此时应适当调节微波场强或波导长度以达到设计输出能量。

2.2 微波场强对输出电子束参数的影响

取电子束注入能量为0.1 MeV，波导长度l=1.062 m，此时γmax=5.38(Wmax=2.24 MeV)，初始轴向磁场B0=0.056 T。微波场强的幅值为Epeak。电子束能量变化趋势、能量增益ΔW、输出能量W1、回旋圈数、渡越时间、轴向速度增益Δvz及横向速度增益ΔvT的结果列于表3。

表3 微波场强对输出电子束参数的影响Table 3 Effect of microwave amplitude on output parameter of electron beam

由表3知，当微波场强较小时，电子输出的能量随加速电场幅度的增强而增加。当微波场强超出一定的阈值后，电子与微波场逐步失谐，电子输出能量变低。当微波场强极大时，电子的横向速度越大，磁镜效应较明显，使电子反向。因此，适当增大微波场强能加强加速梯度，使得电子束输出能量增大(Epeak=7 MV/m时电子束输出能量为2.03 MeV)。

2.3 波导长度对输出电子束参数的影响

由表3可知，电子束注入能量为0.1 MeV、Epeak=7 MV/m时电子束输出能量最大。在此基础上改变CARA加速腔波导长度，并优化轴向静态磁场分布。电子束能量变化趋势、能量增益ΔW、输出能量W1、回旋圈数、渡越时间、轴向速度增益Δvz及横向速度增益ΔvT的结果列于表4。

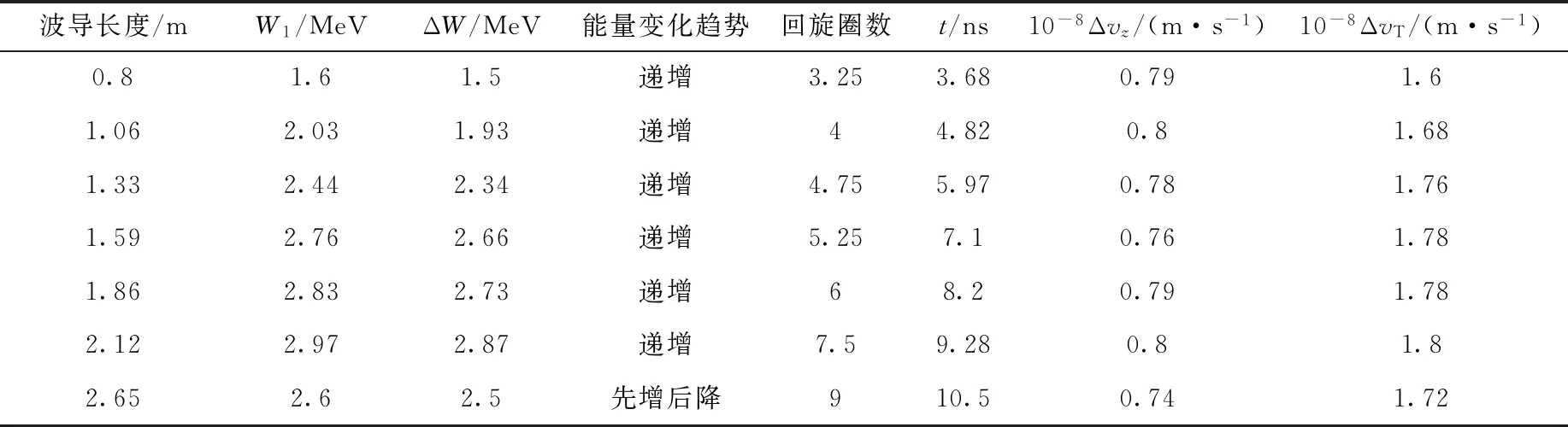
表4 波导长度对输出电子束参数的影响Table 4 Effect of waveguide length on output parameter of electron beam

表4表明，电子束注入能量及微波场强一定时，初始轴向磁场和回旋圈数不变，电子束的输出能量随波导长度的增加而增长，因为在准同步情况下，渡越时间越长，电子受到加速时间越长。但波导长度超过一定的阈值时，电子与微波场的失谐变大，直至最后减速。基于此参数，仿真得到的最大输出能量约为3 MeV，略大于理论上限的近似值Wmax=2.24 MeV(γmax=5.38)。

2.4 电子束输出能量的联合优化

以上仿真结果表明，电子束的输出能量增量受电子束的注入能量、微波场强、波导长度、轴向磁场等多个条件约束。为获得最大输出能量和较高的加速效率，需对这些参数进行合理的联合优化。选定电子束注入能量为0.1 MeV，首先逐渐增大微波场强并优化轴向磁场，直至电子束输出能量不再增长，选定微波场强为7 MV/m；然后逐渐增大波导长度并优化轴向磁场，直至电子束输出能量不再增长，选定波导长度为2.12 m。优化后波导长度、微波场强及电子束输出能量结果列于表5。仿真优化后的结果如图1所示。

表5 联合优化后的参数Table 5 Jointly optimized parameter

由图1a可见，轴向静态磁场随轴向距离先递增，后不变。图1b是某一时刻横截面上的电场和电子分布，蓝色实线为横截面上的横向电场分布，红点为该时刻电子与横向电场作用点，红色虚线圆为电子轨迹。在准同步加速过程中，电子与横向电场在加速相位上，电子束在轴向静态磁场的作用下与TE11模的横向电场一起旋转并获得连续加速。图1c表明在旋转加速过程中，γ随时间几乎呈线性增长。图1d表明电子的轴向速度vz及横向速度vT在加速过程中均增加，且横向增量远大于轴向增量。图1e表明电子轨迹呈螺旋状前进，回旋半径逐渐增大，能量逐渐升高。

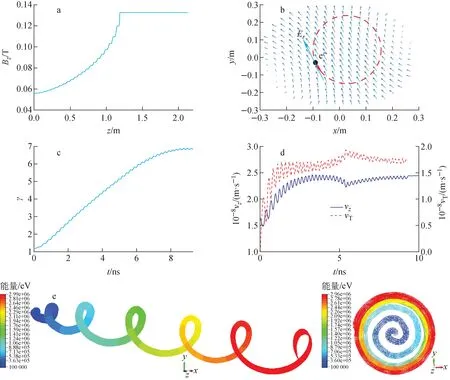
a——轴向静态磁场分布；b——横截面上TE11模电场与电子分布；c——γ随时间的变化；d——vz及vT随时间的变化；e——电子束三维轨迹图1 仿真优化的结果Fig.1 Optimized simulation result

3 结论

通过对CARA的理论分析和建模仿真，研究了加速器的输出能量与相关参数的约束关系。结果显示，CARA中的能量上限不仅与电子束注入能量及折射系数有关，还受波导长度、微波场强及轴向静态磁场的限制。当电子与微波场处于准同步状态时，轴向磁场呈递增趋势，电子在轴向磁场的作用下与TE11模的横向电场一起旋转并获得加速，且回旋半径逐渐增大，能量近似线性增大，绝大部分微波能量通过TE11模式的横向电场传递给了电子束的横向分量。