基于射频偏转腔的束团长度测量系统
白 金,陈曲珊,樊宽军
(华中科技大学 强电磁工程与新技术国家重点实验室,湖北 武汉 430074)
束团长度是高性能电子加速器束流参数的重要指标之一,尤其是在自由电子激光领域,往往需要通过相位调制、磁压缩等技术来获得亚ps级的超短电子束团,从而提高自由电子激光的增益和亮度。因此,束团长度测量对了解此类机器的运行状态、优化运行参数有重要意义。目前,针对超短电子束团长度测量的方法主要有相干辐射光谱法、条纹相机法、射频偏转腔测量法等[1-3]。偏转腔测量法直接以束流本身为被测量信号,可实现单发测量,在稳定性和普适性上具有一定优势,因而被各类加速器机构深入研究[4-10]。本文建立基于偏转腔的束团长度测量系统的模型,对该模型的约束条件进行分析,为计算束团长度提供理论依据。采用粒子跟踪软件Parmela进行束流动力学模拟,根据仿真结果计算测量点的束团长度,验证理论结果的正确性。
1 测量模型

图1 偏转腔束团长度测量系统模型Fig.1 Model of bunch length diagnostic system based on deflecting cavity
偏转腔对束团不同纵向位置的粒子施加不同的横向踢力,使得束团的纵向长度与横向偏转角产生对应关系,偏转腔束团长度测量系统的模型如图1所示。电子束经过偏转腔作用后,漂移至下游荧光屏上成像。若采用薄透镜近似模型,偏转腔的作用可由其中心产生的单次剪切力近似描述[2]。假设偏转腔系统中腔体的纵向长度为D,腔体与电子枪之间的距离为D0,与荧光屏之间的距离为L。本文以驻波矩形腔为例,谐振模式为TM120模,工作频率为2 856 MHz,依靠磁场对粒子进行偏转。可假设束团中心经过腔体中心时磁场相位为0(约定磁场作正弦变化)。利用偏转腔束团长度测量系统的模型,通过测量荧光屏处(C点)的束团横向尺寸倒推出偏转腔出口处(B点)的束团偏转角,再找到这一角度与偏转腔入口处(A点)束团长度的对应关系,由此计算出束团长度。在实际测量中,需分别测量偏转腔在工作状态(on)和非工作状态(off)时荧光屏上的束团横向尺寸[11-13]。
1.1 A点到B点
偏转腔出口处粒子的工作状态可用入口处粒子的工作状态来表示。根据束流传输理论和偏转腔工作原理,可将偏转腔的传输矩阵Rd表示为:
(1)
束流矩阵的变换关系可表示为:
(2)
其中:σ0为束团进入偏转腔前的束流矩阵;σ为束团经过1个束流传输元件后的束流矩阵。记束流传输矩阵元为σmn,并用上标A、B、C表示不同位置处的束流矩阵参数,用上标on和off分别表示偏转腔工作状态与非工作状态时的束流矩阵参数。由式(1)、(2)可得到:
(3)
(4)
(5)
当偏转腔处于非工作状态时,整个腔体等效为长度为D的漂移段,根据束流传输理论,其偏转方向的传输矩阵RL可表示为:
(6)
则由式(2)、(6)可得到:
(7)
(8)
(9)
由以上关系可知,B点的粒子状态可用A点的粒子状态表示,所研究的问题则可转化为求解B点粒子状态和C点粒子状态之间的关系。
1.2 B点到C点
从B点到C点的距离为L,其传输矩阵同式(6)。根据式(2)可得到:
(10)
当偏转腔处于非工作状态时,荧光屏上束流矩阵参数有相似的表达形式:
(11)
用式(10)减去式(11)可得到:
(12)
将式(3)~(5)、(7)~(9)代入式(12)得到(一般的束团满足σ15=σ25=0):
(13)
将荧光屏上测得的偏转方向上的束团横向尺寸与偏转腔入口处束团的纵向长度建立联系,只需解得偏转腔传输矩阵中的矩阵元R25,即可求出束团的长度。可由束流传输理论得到偏转腔处于工作状态和非工作状态时,束团产生的偏角之差Δy′为:
Δy′=R25σz
(14)
其中,σz为束团纵向尺寸的均方根值。这一偏角差值可用横向动量与纵向动量的比值表示为:
(15)
其中:p⊥为束团横向动量;pz为束团纵向动量;q为粒子电荷量;k为偏转场的波数;c为自由空间中的光速;Vd为偏转电压有效值;φ为束团中心在经过腔体中心时的相位。当满足λ远大于σz且φ=0时,利用式(13)~(15)可推导出束团长度σt计算公式为:
(16)
其中,ω为偏转场的角频率。根据束流传输理论,束团长度的测量公式也可表示为:
(17)
其中,σon和σoff分别为偏转腔处于工作状态和非工作状态时偏转方向上的束团横向尺寸。
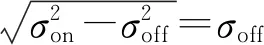
(18)
在分析过程中,用到4个近似条件:1) 初始束团z方向与x方向无耦合关系(σ15=σ25=0),这一条件在一般束团中均能得到满足;2) 认为束团在经过偏转腔后,其能量偏差项对其偏转方向无影响(R16=R26=0);3) 束团中粒子的纵向位置的不同不会对偏转方向上的偏移造成影响(R15=0),实际上,这一参数是粒子相位φ的函数,当φ=0时,R15恒等于0;4) 自由空间中的波长λ远大于束团长度,当工作频率为2 856 MHz时,波长约为105 mm,而一般所测的束团长度都在10-1mm量级,这一条件也可满足。
2 矩形单腔体优化
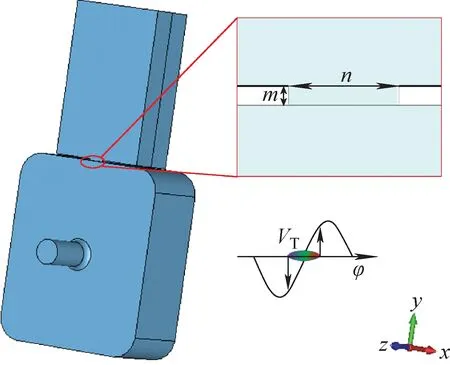
图2 腔体与耦合器连接模型Fig.2 Connection model between cavity and coupler
本文设计的目标是在束流能量为10 MeV、初始束团横向尺寸为0.3 mm、偏转腔测量系统长度小于1 m、馈入功率不高于1 MW时,偏转腔系统的时间分辨率优于200 fs。根据式(18),可计算出所需的偏转电压至少为1.1 MV。在三维电磁场仿真软件CST中建立矩形偏转腔模型并进行仿真。考虑到真实的偏转腔应用场景,将圆倒角、束流管道、耦合器等对场分布有影响的因素考虑在内进行模拟。由于偏转腔中依靠磁场偏转束团,对束流不做功,也不存在束流负载效应,因而为了将微波功率更好地馈入到腔体中,耦合器的最佳耦合度应为1。耦合器与腔体的连接如图2所示,耦合度主要通过修改耦合孔的尺寸进行调节。设定耦合孔的宽度为n,高度为m,由于耦合孔高度将影响连接处的机械强度,故综合考虑后选择m=1 mm。用CST进行仿真后发现,当n=10.16 mm时,反射系数最小可达-36 dB,对应的耦合度为1.05。确定偏转腔结构后,通过选择合适的功率源、偏转腔与荧光屏距离等系统参数,来实现所需的分辨率[14-16]。优化后的偏转腔束团长度测量系统参数列于表1。考虑到该系统的长度要求小于1 m,漂移段长度选择L=0.8 m。当馈入功率为1 MW、谐振模式为TM120模、工作频率为2 856 MHz时,最优的矩形腔腔体尺寸为120.59 mm×106.64 mm×47.25 mm,此时偏转腔能达到的最大偏转电压为1.2 MV。根据式(18),偏转腔系统的时间分辨率可达182 fs,在理论上满足设计要求。

表1 偏转腔束团长度测量系统参数Table 1 Parameter of deflecting cavity bunch length diagnostic system
3 束流仿真
将CST仿真得到的电磁场数据导入Parmela后,即可进行粒子跟踪。束团参数列于表2,图3为当偏转腔处于不同工作状态时荧光屏上对应的束团横向尺寸,在偏转方向上,这一尺寸从0.3 mm增加到0.88 mm。根据式(17),可计算得到初始的束团长度为504 fs,这一计算值与理论值之间有0.8%的误差。
这里需要说明的是,在进行束流动力学模拟的过程中,发现当束团中心参考粒子相位设置为理想相位后,下游荧光屏上得到的束团仍有一段较小的横向偏移。通过研究偏转场对粒子的作用过程发现,参考粒子在通过驻波偏转场时,不同纵向位置处的场相位不同,虽然在理想相位下注入可保证参考粒子通过偏转腔后的横向动量增量为0,但横向位置偏移不为0,该偏移在束团下游漂移过程中也一直存在,但由于这一较小的偏移对束团横向尺寸的测量几乎没有影响,因此可忽略不计。当束团注入相位为非理想相位时,计算所得束团长度与参考粒子偏离中心线距离如图4所示。相位的偏差对荧光屏上束团横向尺寸造成的影响可忽略不计,即此时计算得到的束团长度不会有太大误差。但需注意的是,相位偏差会对参考粒子在下游荧光屏上的位置造成很大的影响,当参考粒子远离束流中心线时,会给实际测量束团横向尺寸带来一定困难。

表2 束团参数Table 2 Bunch parameter

a——非工作状态;b——工作状态图3 荧光屏上的束团横向尺寸Fig.3 Transverse size of bunch on screen
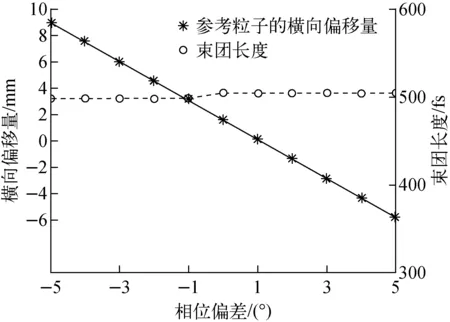
图4 束团长度与参考粒子偏离中心线距离Fig.4 Bunch length and reference particle off centerline distance
4 小结
本文通过建立基于RF偏转腔测量电子束团长度系统的模型,从束流的角度对偏转腔测量束团长度的理论进行推导,为束团长度的计算提供依据。用三维电磁场仿真软件CST进行仿真,得到了最优的单腔腔体尺寸和最优的耦合器尺寸,偏转腔测量系统的时间分辨率达到182 fs,满足了设计要求。将仿真得到的场分布导入Parmela软件中进行粒子跟踪,分析了束团在荧光屏上产生横向偏移的原因,验证了理论结果的正确性。

