半干旱草原型流域土壤入渗过程及转换函数研究
黎明扬,刘廷玺,2,罗艳云,2,段利民,2,张俊怡,周亚军
(1.内蒙古农业大学 水利与土木建筑工程学院,内蒙古 呼和浩特 010018;2.内蒙古自治区水资源保护与利用重点实验室,内蒙古 呼和浩特 010018)
1 研究背景
土壤入渗是生态水文循环过程中水分运移的重要组成部分,是降水通过土壤向地下水转化的必然过程[1]。我国对于土壤入渗的研究开展的较早,主要集中在东部和观测设施较为完备的流域[2-3],例如Sun 等[4]收集了我国较为湿润的东部和南部42 个地区不同植被和土地利用类型下的土壤入渗数据,分析了大尺度下土地利用变化对土壤入渗速率的影响,并指出建立混农业林生态系统有利于提高农田和人工林的土壤入渗能力;Wang 等[5]在黄土高原退耕还林后的土壤上进行了生物土壤结皮对土壤入渗特性时间的变化研究。而位于我国北部以锡林河、巴拉噶尔河等为首的草原型内陆河流域开展的研究不多且不深刻,尤其是近些年在气候变化与过度放牧二者的双重影响下,原本生态脆弱的草原更是面临严峻挑战[6-7],因此探索和揭示干旱半干旱地区草原型流域特殊的生态水文过程和水分转化运移机制及其影响因素,对进一步开展生态环境的保护和退化草场的治理工作具有重要意义。
传统的大规模试验费时费力且破坏性大[8-9],而土壤传递函数(Pedo-Transfer Functions,简称PTFs)则可利用有机质含量、容重、粒径组成等土壤基本特性指标,间接计算出常用的土壤水分特征参数和曲线[10],在较大尺度的土壤入渗特性研究中是十分必要的,该方法可以在提高试验效率的同时减少取样对环境的破坏。为此,本文采用野外原位土壤入渗试验与原状土采样获取试验数据,通过参数拟合选择最能精确反映地区入渗过程的模型并利用其模拟稳定入渗率,利用主成分和相关性分析研究影响水分下渗的因素,建立了土壤入渗特性与入渗环境要素之间的土壤转换函数,并在此基础上联合同期土壤生态调查数据在小流域尺度上进行了稳定入渗率的大面积预测。
2 材料与方法
2.1 研究区域概况本研究选择内蒙古高原半干旱的锡林河流域为研究区,其位于内蒙古自治区中部锡林郭勒盟,发源于赤峰市克什克腾旗宝尔图山,流经锡林郭勒盟阿巴嘎旗,在贝力克牧场转向西北流经锡林浩特市,最终注入查干诺尔沼泽地自然消失[11]。开展野外试验的区域位于锡林河支流浩勒图郭勒与干流锡林高勒河交汇处以上流域(43°24″—44°4″N,116°2″—117°15″E),面积为1852 km2,区域地势三面环山,超过90%的植被为天然牧草,以茅针和羊草最为常见。研究区属中温带半干旱大陆性季风气候,多年平均降水量为266.8 mm,其中,6—8月降水量占年总降水量的50%以上[12]。
2.2 试验设计首先利用中国1∶100 万土壤类型图划分出试验区包含厚栗黄土、草甸沼泽土、草原风沙土、石灰性草甸土、淡黑土共五种土壤类型分区,按照每种土壤类型占试验区面积比例,设置数个具有地区代表性的试验点,包括土壤入渗试验点38 个,土壤生态调查点62 个。土壤入渗试验点和生态调查点分为7 组,其中6 组布设成垂直于河流与等高线的断面,另设1 组覆盖前6 组未包含的土壤、植被及土地使用情况;所有点位包含了该区域9 种土地利用类型、4 种植被类型、90%以上的海拔、坡度坡向及生物生长状况(图1与表1)。

图1 研究区位置及采样点分布

表1 研究区土壤特性及所含采样点个数
为避免晨露和降水对土壤初始含水率(Initial Moisture Content,简称IMC)的影响,所有试验于天气连续晴朗的2018年7月26 至30日的10 至16 时进行,使用手持GPS 记录实际采样点经纬度坐标,在去除地表浮土及植被后进行,试验期间未发生降水。入渗试验使用双环入渗仪,入渗前,在入渗环四周利用土钻取土,每10 cm 一层共取5 层,用于测定IMC;入渗过程中,记录内环及两个马氏瓶水位变化,前20 min 每1 min 读数一次,20 min 后每3 min 读数一次;试验结束后,在距入渗环30 cm 处挖深于入渗深度的剖面(对于入渗深度不足50 cm 的点位则按照50 cm 开挖剖面),从表层向下取样,每10 cm 一层共取5 层,每层采用100 cm3的环刀和自封袋各重复取样3 个,分别用于测定土壤容重(Bulk Density,简称ρ)、粒径组成、有机质(Soil Organic Matters,简称SOM)、地下生物量(Underground Biomass,简称UB)及其他土壤理化特性。各土壤生态调查点按照入渗试验中的标准开挖50 cm 深的剖面取土,用于测定IMC 及各土壤理化属性。土壤粒径利用HELOS & RODOS 激光粒度分析仪进行干法测定,分级标准采用美国制:砂粒(2~0.05 mm,Sand Content,简称SA),粉粒(0.05~0.002 mm,Silt Content,简称SI),黏粒(<0.002 mm,Clay Content,简称CL);平均粒径大小(Average Particle Size,简称APS)通过SA、SI、CL 三种颗粒所含百分比乘以每种颗粒的平均粒径计算获得;ρ采用环刀法测定;SOM 采用浓硫酸-重铬酸钾外加热法测定;IMC 采用恒温箱烘干法测定;UB 采用烘干称重法测定。
2.3 入渗模型及评价方法土壤入渗模型可以模拟时间与入渗量之间的关系,研究选择Green-Ampt、Philip、Kostiacov、Horton、Mezencev 及USDA-NRCS 六种入渗模型对双环入渗过程进行模拟[13-18],见表2,使用Matlab 的Curve Fitting tool 进行参数拟合,最佳模型参数是通过计算比较不同参数的最小平方误差决定的,将模拟参数带入选择的6 个入渗模型中,分别计算与实测数据相同记录时间的累计入渗量。为了更好地识别多元非线性拟合中自变量个数对模型R2的影响[19],本文使用Adj-R2和RMSE 对入渗模型的模拟精度及误差进行评价。

表2 土壤入渗模型
3 结果与讨论
3.1 试验数据的统计特征对于整个研究区而言,土壤水分的入渗速率很快,单位面积平均稳定入渗率达0.2 cm/(min·m2);入渗初期速度的衰弱比例较高,前5 min 和20 min 分别达到76.60%与92.55%;整个入渗过程稳定较快,20 ~60 min 内即可达到稳定,这也侧面说明了研究区这种砂质草甸地土壤垂向的成分和结构比较稳定。由于入渗中后期的入渗速度衰减明显,研究使用入渗总量的对数形式表示其随时间变化的关系(图2),由图可知荒漠风沙土的入渗总量和速率最大,草甸沼泽土最小,仅有荒漠风沙土的三分之一,而其余三种类型土壤有较为接近的入渗过程。
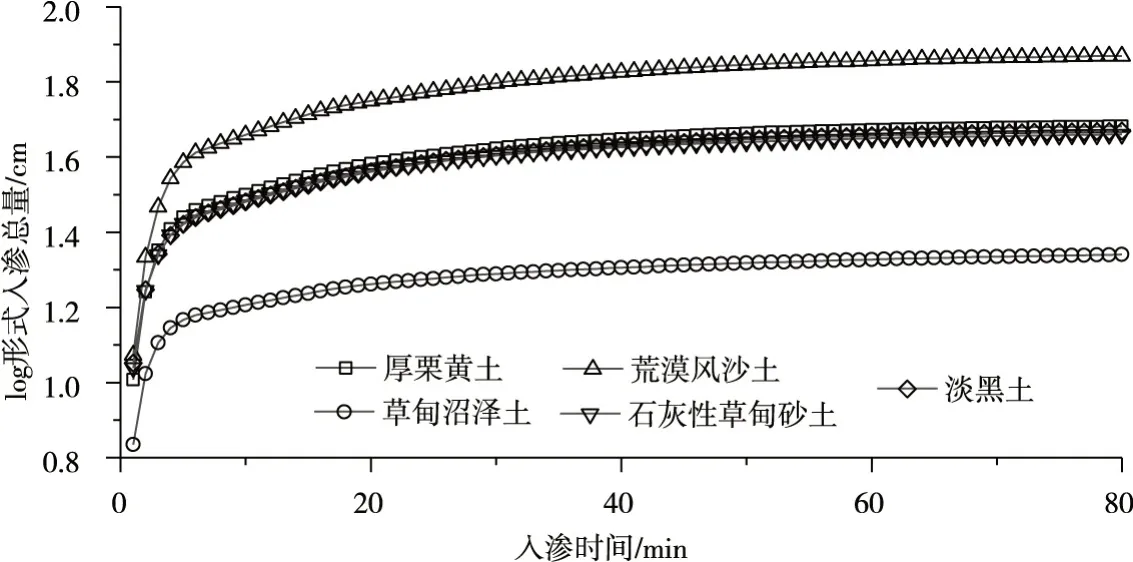
图2 入渗时间与log 形式入渗总量的关系
研究区表层土壤基本理化特征如图3所示,根据粒径组成,研究区主要属砂质土壤,APS 均在75 μm 以上,较高的SA 使得整体ρ偏高,荒漠风沙土在五种土壤类型中各层位的APS 最大为93.77 μm。土壤IMC 与采样点位到河流的距离关系密切,分布在河流两侧的草甸沼泽土和石灰性草甸砂土的IMC明显高于其他三种离河较远的土壤,尤其是分布在干流的草甸沼泽土,其各层土壤的平均含水率最高达到26.6%。在随深度变化方面,各类型土壤的APS、IMC 和ρ变化不大,该结果与Zhang 等[20]和Yu等[21]对半干旱区植被与土壤理化性质关系的研究结果近似。降雨次数和降水量稀少使得土壤长期处于干旱状态,主要分布在平坦地区的草甸沼泽土、石灰性草甸土以及淡黑土三种土壤的SOM 随深度增加呈下降趋势,而主要分布在山地的厚栗黄土,其SOM 在20 cm 土层有明显增高,这是因为植物为了生长在畜水困难的坡地上,深层表土根系更加发达,拥有大量毛细根的20 cm 土层经过常年的积累SOM 有明显提高[22]。

图3 5 种土壤粒径、含水率、容重及有机质含量随深度变化规律

表3 五种土壤类型下6 个入渗模型模拟参数值

表4 入渗模型模拟精度及误差
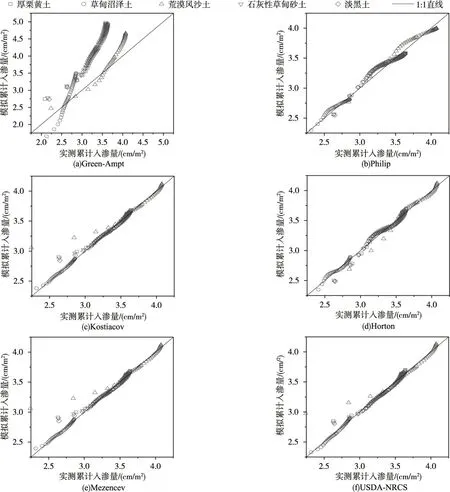
图4 五种土壤类型下6 个入渗模型模拟累计入渗量与实测值对比
3.2 入渗过程模拟各入渗模型的模拟值与实测值对比、模型参数及模拟结果的精度和误差评价如图4、表3与表4所示。
结合图表可知,经验模型的拟合效果要明显优于理论模型,这是由于理论模型对于实际状况进行了概化和一定程度的简化[23-24],在模拟情况相对简单的入渗过程时误差较小,例如荒漠风沙土在研究区的5 种土壤类型中植被稀疏,SOM、IMC 和UB 都处于较低水平,Green-Ampt 模型对其入渗过程的模拟误差是该模型模拟5 种土壤中最小的,而其他4 种类型的土壤情况则相对复杂,模拟误差也随之增大(图4(a)),此外Green-Ampt 模型在研究区整体模拟效果较差,研究判断导致该结果的原因可能有以下两个:(1)湿润锋面在砂粒含量较高、入渗速率较快的砂质草甸地并不是垂直推进的,这与Clemmens 的看法相似[25];(2)研究用于模拟推导出的入渗时间t 与入渗总量I(t)间的隐函数不适合使用MATLAB 的Curve Fitting tool 进行参数模拟。相比于理论模型,经验模型更注重时间与入渗量之间的数学关系,尤其是在入渗过程的中后期模拟效果都比较优秀[19]。
Horton 和USDA-NRCS 模型的综合表现最佳,二者拟合结果Adj-R2均高于0.9 且RMSE 均小于0.1,说明以上两种模型在不同土壤类型的模拟中均具有较好的普适性,该结论同国内外部分学者的研究结果一致[19,26-27];Kostiakov 和Mezencev 模型在入渗前期的模拟有一定出入,尤其是在含砂量较高的地区表现较差,这是由于以上两个模型缺少用来描述初始入渗速率的常数项,而Mezencev 模型作为Kostiakov 模型的改良,其模拟精度与误差却均略低于Kostiakov 模型,说明砂质土壤入渗前期的高渗透性和较快的入渗速率下降比例会影响Mezencev 模型对于K ′参数的估计,这与Furman 等[28]在改良Kostiakov 模型渗透性能的研究结果近似。
Horton 模型的fc参数虽然是经验模拟值,但是比较接近真实的稳定入渗率[29],同时由于Horton 模型考虑了初始入渗速率,对于刻画干旱半干旱型草原土壤前期入渗速度快、稳定入渗时间短的特殊入渗过程最为贴切,因此研究选用Horton 模型推求各点位的稳定入渗率以供下文入渗特征值的变异性分析及土壤转换函数的建立使用。
3.3 影响因素分析土壤入渗过程受粒径、ρ、SOM、IMC、UB 等因素的影响[30-31]。研究对38 个入渗点位的土壤理化性质及入渗环境条件进行了主成分分析,并统计了观测尺度上入渗特征值与影响因素的变异系数和相关性,由于瞬时入渗速率较小,难以精确测量,尤其是50 min 之后的入渗速率,其也是通过一次测量多分钟的累计入渗量后取平均获得的,因此研究选用30、50、80 min三个时刻的累计入渗量和稳定入渗率作为入渗特征值从而代表入渗过程,主成分分析结果如图5所示。
主成分分析可以获得两个包含77.2%原始信息的主成分,研究将其分别命名为与土壤密实程度和孔隙分布相关的土壤自身物理属性及与入渗液体动能势相关的外界环境成分(图5)。结果表明,主要分布在排列图左侧的入渗点位水分运移迅速,较大的APS 和较高的SA 增加了土壤的ρ,同时由于试验点地理位置的原因,分布在序列图第四象限点位的试验时间也基本在中午,较高的水温也会降低水的黏滞性[32],土壤与温度二者共同提高了入渗速率。分布在河道附近的点位主要分布在序列图的第一象限及距其较近的二四象限,这些点位的IMC 均超过26%,这不仅会降低土壤的入渗速率,还会促进植物的生长,导致SOM 和UB 达到研究区其他干旱区域的2 倍以上。有机质可以促进土壤中的小颗粒形成水稳性土壤团聚体,其中一部分直接填充在土壤毛管与孔隙中,阻碍了水分的渗透,这与Liu 等[32]和Wang 等[5]对有机质影响入渗的研究结果一致;另外干旱半干旱地区的植物根系发达,具有固水固土的作用,可以减缓土壤水分的运移,这与Wu 等[33]在干旱草原上植被对土壤水文过程的影响研究结果相同。
变异系数描述了变量组间变异性的大小,CV≤0.1 时为弱变异性,0.1<CV<1 时为中等变异性,CV≥1 时为强变异性。由表5可以看出,研究区土壤理化性质的整体变异性中等偏弱,不同试验点的累计入渗量具有中等变异性,且该差异性有随着时间推进逐渐增大的趋势;除了由于含量较低所引起变异剧烈的CL 外,土壤自身物理属性的变异性不大,而与入渗液体动能势相关的外界环境成分,如IMC、UB 以及SOM 三者的变异系数相对较大,说明研究区的累计入渗量和稳定入渗率可能主要是由土壤非自身物理属性的空间变异造成的。

图5 土壤理化性质及试验条件的主成分序列图

表5 入渗特征值与影响要素的统计特征
入渗特征值与影响要素的相关性分析结果显示,累计入渗量和稳定入渗率与SA、APS 及Temp 成显著正相关,与SI、CL、ρ、SOM、IMC 和UB 成负相关关系,该结果与刘继龙等[34]在观测尺度上土壤入渗特性与影响因素的相关性分析结果趋势一致。由于研究区SI 和CL 均处于较低水平,SA 和APS与所选入渗特征的相关性接近,研究认为在研究区APS 对于土壤的粒径组成有较好的代表性;SOM和IMC 与累计入渗量的相关性较高,与稳定入渗率的相关性相对较低;而Temp 的相关性趋势则相反,其与稳定入渗率的相关性最高。
3.4 土壤转换函数基于大量有关入渗特征值与影响要素建立PTFs 的研究可知,入渗特征值与影响要素之间有较好的对数关系[35-36]。文章首先使用观测尺度上所有的影响要素与累计入渗量和稳定入渗率建立对数关系的多元非线性PTFs(式(1)),结果显示稳定入渗率的转换函数模拟效果优秀,而累计入渗量的模拟误差略大。为了进一步简化PTFs,研究基于表5中相关性分析得出的结果,筛选出ρ、APS、SOM、IMC、UB 及Temp 等6 个与入渗特征值显著相关的影响要素重新建立简化的PTF(式(2))。两种不同形式PTFs 的具体形式及评价结果如表6所示。
草原型流域土壤颗粒总体较粗,表层风化层较薄土质相对均一,有机质含量低且土颗粒不易形成团粒结构,经过简化的PTF 精度虽略有下降,但稳定入渗率的模拟结果依然良好,说明在入渗环境相对简单的干旱半干旱型草原,通过土壤理化性质及环境变量建立来模拟土壤入渗特征值所建立的PTFs 形式简单,可以简化且适应性较好。然而由于试验中缺乏对相同点位不同土壤初始含水率的采样,而土壤含水率相比于土壤理化属性,其在短时间内的变化更明显,讨论其对PTFs 参数的影响程度在实际应用中尤为重要;初始入渗速率和累积入渗量会直接因其改变了入渗水流湿润区的平均梯度而发生改变,而稳定入渗率则更稳定,在参数的敏感性分析中更有意义,因此研究分别选择初始含水率增加或减少5、10、15、20%以及无变化9 种情况下,两种PTFs 计算fc的参数进行分析,结果如图6所示,分析中当土壤含水率低于残余含水率时取残余含水率,高于饱和含水率时取饱和含水率,残余含水率与饱和含水率分别取研究区平均值3.5 与38.9%。

图6 不同初始含水率对简化PTF 参数的影响

表6 不同影响因子土壤转换函数参数与评价
结果显示,当含水率有较大幅度降低时,PTFs 参数大都随之改变,其中常数项a 与土壤颗粒组成及粒径相关的参数b、c、d、f 有明显变化,表明土壤初始含水率对PTFs 参数影响剧烈,当在较低含水率的情况下使用PTFs 应当适量增加试验,以减小模型误差。整体来看,土壤初始含水率的变化对未简化的PTF 计算fc的影响较大,对简化的PTF 影响较小,说明简化的PTF 可以在一定范围内更好地适应土壤初始含水率的变化。
研究使用在入渗试验同期对62 个土壤生态调查点的采样数据(图1),联合38 个土壤入渗试验点数据,绘制了研究区小流域尺度上较为精细的PTFs 输入参量的面尺度插值拓展,并分别使用相同1 km×1 km 大小的栅格绘制了使用Horton 模型和PTFs 预测的研究区土壤稳定入渗率分布图(图7(a)和图7(b)),并对二者的预测结果进行了比较(图7(c)),其中图7(b)假设试验水温恒定为20 ℃。
结果显示,PTFs 预测的研究区土壤稳定入渗率分布图更贴合实际,该分布趋势与黎明扬等[22]在使用合成孔径雷达和PTFs 联合反演锡林河上游表层土壤饱和导水率的研究结果一致。由于Horton 模型只能模拟试验点位的稳定入渗率(图7(a)),因此相较PTFs 预测的结果(图7(b))其不仅损失了大量细节,在区域模拟的极值表现上也存在较大差异。在两河交汇的湿地地区,PTFs 预测的稳定入渗率低至不足0.001cm/(min·m2),而Horton 模型在此处的预测值过高;两河中部虽属荒漠风沙土,但该地区仅生长着少量贫瘠的牧草,其实际入渗率要高于Horton 模型的预测值(图7(c)),尤其是在研究区中部入渗率极高的裸露沙地,Horton 模型有较大程度的低估;整体来看,Horton 模型表现过于片面,少量的点位不足以把控整个研究区的入渗特征。

图7 两种模型预测稳定入渗率分布及对比图
使用PTFs 大面积预测土壤入渗特征值也存在一些不足,例如对下垫面环境等影响要素考虑不全面、简化PTFs 带来的精度缺失以及原位采样带来的空间限制等。前文提到,影响入渗过程的要素多且相互联系,气压、空气温湿度等气候条件,土壤孔隙度与相同类型土壤下不同的压实程度都会对入渗过程产生影响[37];粒径组成、植物根系的量与分布状态都与ρ息息相关,由此角度分析,单纯通过相关性等要素分析筛选PTFs 的输入参数略显片面,通过构建一个或多个综合性的影响要素指标或许可以从机理上描述入渗条件与入渗特征值之间的转换关系;结合遥感技术可以在一定程度上弥补原位采样的空间限制并精细刻画土壤物理要素的分布,但其对于深层土壤参数的获取仍表现出较大的局限性[22],尤其是在土壤属性纵向变化较大的地区具有一定的不确定性。
4 结论
(1)半干旱型草原土壤砂粒含量高,水分入渗迅速,单位面积平均稳定入渗率达0.2 cm/(min·m2)。使用6 种入渗模型对5 种土壤类型下38 个点位的入渗过程进行模拟,结果表明,Horton 和USDA-NRCS 模型在研究区的综合表现最佳。
(2)天然草原入渗过程受外界干扰相对较小且影响要素的空间变异性呈中低等水平;主成分分析可以将9 个影响要素压缩成2 个包含77.2%原始信息的主成分,研究分别命名将其为与土壤密实程度和孔隙分布相关的土壤自身物理属性及与入渗液体动能势相关的外界环境成分;相关性分析结果显示ρ、APS、SOM、IMC、UB 及Temp 等6 个影响要素与入渗特征值显著相关。
(3)研究分别通过使用全部影响要素和6 个显著相关的影响要素与入渗特征值建立PTFs,结果显示入渗特征值与影响要素间有较好的对数关系,使用显著相关影响要素建立的PTFs 精度虽略有下降,但稳定入渗率的模拟结果依然良好;使用Horton 模型和简化的PTF 分别对研究区土壤的稳定入渗率进行模拟,结果表明,Horton 模型的预测结果不仅损失了大量细节,在极值的表现方面也存在较大的局限性;使用PTFs 预测小流域尺度土壤入渗特征值有助于提高试验效率,减少环境破坏,该方法在复杂入渗环境下的鲁棒性尚不明晰,有待于进一步研究。

