确定性地震动空间差异对重力坝地震响应影响研究

何卫平，熊 堃，卢晓春

（1.三峡大学 湖北省水电工程施工与管理重点实验室，湖北 宜昌 443002；2.长江勘测规划设计研究有限责任公司，湖北 武汉 430010；3.三峡大学 水利与环境学院，湖北 宜昌 443002）

1 研究背景

我国西南地区高坝密集，地震风险高。自2008年汶川地震以来，在西南地区发生的震级不低于7.0 的地震有2010年青海玉树地震、2013年四川芦山地震、2017年四川九寨沟地震等。强震不仅造成人员伤亡和经济损失，也严重威胁高坝安全［1］。研究高坝在强震作用下的地震响应，评估高坝的抗震安全度是保障工程安全运行须解决的关键问题之一［2］。随着实测地震记录资料的积累，强震引起的场址地震动存在空间差异逐渐成为共识［3］，在高坝等大跨度结构的地震响应分析中考虑输入地震动的空间差异成为发展趋势。

目前，空间差异地震动场主要见于地震工程学中的地震动输入模型和强震地震动场等研究领域。在地震动输入模型中，波动输入模型和自由场输入模型在完成地震动输入时须首先构建空间差异地震动场。波动输入模型通常结合垂直或倾斜入射假定，依据传播效应将地震运动转化为人工边界上的等效荷载［4］。波动输入模型被广泛用于大坝地震响应分析，杜修力等［5］、岑威钧等［6］、姚虞等［7］分别采用波动输入模型研究非一致运动作用下的大坝地震响应。自由场输入模型通常依据实测地震记录的插值或外推获得空间差异地面运动，进而将空间差异运动转化为作用在模型中结构-地基接触面上的节点力完成非一致地震动输入。由于须以实测地震记录为基础，自由场输入模型通常与河谷布置测站的工程结合应用，如Mojtahedi等［8］、Alves等［9］分别对Pacoima拱坝非一致地震响应的研究，Chopra等［10］对Pacoima 拱坝和Mauvoisin 拱坝非一致地震响应的研究，Wang 等［11］对Pacoima 拱坝在非一致地震动场影响下损伤发展的研究。

强震地震动场研究中将地震动空间差异的产生原因归纳为行波效应、衰减效应、相干效应和局部场地效应［12］，并采用相干函数描述地震动空间差异。目前已有较多的经验和半经验相干函数模型提出［13-15］，工程应用中须在相干函数基础上通过互功率谱矩阵获得空间差异地震动场［16］。由于相干函数侧重经验性描述，没有从物理机制考察地震动的空间差异［17］，一些学者从物理机制出发提出地震动场模型。金星［18］提出的随机地震动场模型，采用参考点地震动近似表示地震对场址范围内地震动场的影响和控制，通过等效相速度的随机涨落刻画小范围内测点地震动的空间差异，并考虑了地震波衰减、频散、入射方向等因素。张翠然等［19］提出的随机有限断层法，将潜在震源的主干断层分为一系列可作为点源的子断裂，采用具有一定模态和时间序列的破裂模拟地震发生过程，顺序叠加各点源对坝址的作用给出近场强震的坝址地震。贺春晖等［20］通过建立震源-传播介质-坝址峡谷场地的数值模型，模拟地震波从发震断层破裂开始到坝址场地的物理过程，生成坝址区三维地震动场。王鼎等［21］将地震动场区分为大小两个尺度描述，在大尺度上采用点源和均匀介质模拟震源和传播效应，在小尺度上采用随机介质模拟局部场地性质并获得地震动随机场。

实测地震资料显示，地震动的空间差异极为复杂。在宏观特征上，地震动空间差异除包含行波效应引起的时间滞后外，也包含复杂的幅值变化和时程形状差异等［3］。波动输入模型通常只考虑行波效应所引起的时间滞后，无法体现地震运动的复杂幅值变化和时程形状差异，但由于考虑因素少、实现便捷，在工程抗震领域应用广泛。自由场模型可反映地面运动的任意空间差异，但受限于布置测站的工程较少，难以推广至无测站工程。基于相干函数模型获得地震动场的方法，须以互功率谱矩阵生成空间点的地震动，在高坝-地基体系地震响应分析的应用中面临计算量巨大难以实现的难题。考虑物理机制的地震动场模型是目前逐渐发展和推广的研究方向，但已有的地震动场模型在描述空间差异地震动场时，均考虑地震波从震源到场址的完整传播过程。然而，模拟地震波从震源到场址的传播过程存在两个困难：一为震源破裂机制不明，震源产生的地震波难以定量描述；二为传播过程中地质条件难以调查清楚。这两个困难使描述地震波的完整传播过程难度大、准确性低。因此，无论从强震地震动场研究抑或工程应用研究出发，现阶段须解决的核心问题均是在小范围内对地震动场进行解释或模拟［22-23］。

综上，随着强震地震资料的积累，对地震动空间差异的解释和模拟引起越来越多学者的关注。同时，地震工程学中地震动输入模型的研究也亟需既能合理描述地震动空间差异也便于工程应用的地震动场模型。为推动大跨度结构地震响应分析中空间差异地震动场研究的发展，本文将关注重点放在场址小范围区域，在波动输入假设基础上通过引入地震波组合效应表达地震动空间差异的形成机制，并获得可描述运动的时间滞后、复杂幅值变化和时程形状差异的空间差异地震动场。当复杂入射地震波信息确定时，场址范围内的地震动场可定量确定，因此将模型称为确定非一致地震动场模型。为探讨确定性地震动空间差异对结构地震响应的影响，以确定非一致地震动场模型和垂直入射波动输入对应运动场为基础，以重力坝为例对结构地震响应进行比较分析。

2 基于地震波组合的非一致地震动场

2.1 空间差异地震动场的形成机制场址地震动场是震源产生的地震波，经复杂传播介质，到达场址后在复杂地质地形影响下形成的运动场。受到震源分布范围及破裂机制影响，震源产生的地震波通常不止一条；受可能存在的断层、介质层面等影响，传播介质通常会引起地震波数量增加、波型成分变的复杂。且空间内的地震波在持时、传播方向、波函数等方面通常存在差异。当研究范围限定在场址时，场址内的地震动场由入射地震波信息和场址介质信息共同确定。在场址介质方面，目前已可通过地质勘探等技术手段获得较精确的地基介质信息，但在入射地震波方面，目前尚无法精确识别入射波信息。因此，空间差异地震动场的构建主要受限于场址入射地震波信息的描述。

对特定的空间区域，当已知在区域内传播的所有地震波信息时，可通过叠加不同地震波的波函数得到任意空间点的运动时程。受到地震波在波阵面形状、波型类别、传播方向、初至时间等方面的差异，地震波在不同空间位置的叠加方式不同，从而造成质点运动的空间差异，将该现象称为地震波组合效应［24］。从地震动场空间差异的可解读性出发将地震动的空间差异区分为确定性部分和随机性部分。确定性部分指可定量描述的空间差异，主要指源于地震波组合效应的空间差异；随机部分指由地基不均匀或地形不规则引起的难以定量描述的地震动空间差异［24］。考虑地震波组合效应的确定非一致地震动场，除包含波动输入模型通常蕴含的时间滞后特征外，还包含质点运动的复杂幅值变化和时程形状差异，在地震动空间差异方面的模拟更为合理。

2.2 简化处理和入射地震波的随机描述确定非一致地震动场以场址地质地形条件和复杂入射地震波信息为基础，其中地形条件和浅部地基介质信息容易获得，深部地基介质信息和复杂入射地震波信息获取难度较高。考虑到结构地震响应分析对空间差异地震动场的需求，本文参考波动输入模型对问题进行简化处理。

在地质地形假设方面，采用与波动输入模型一致的均匀半无限介质假设。在复杂入射地震波方面，由于目前地震学相关研究成果较少，采用随机模型描述入射地震波信息。随机获得复杂入射地震波信息的物理意义相当于重现地震波由震源传播到场址的过程中，地震波信息逐渐复杂化的演化过程。当随机入射波信息与实际场址出现的复杂入射地震波类似时，通过确定非一致地震动场模型得到的空间差异地震动场具有较高的代表性。由于目前地震学研究中尚未关注场址范围内的复杂入射地震波，本文在总结地震波传播规律基础上对随机生成的入射地震波信息进行控制。

考虑到目前研究针对二维问题开展，假定入射地震波为P 波和SV 波两类波型。结构地震响应关注的地震动场范围通常不超过千米量级，远小于地震影响范围，在场址范围内将球面地震波视为平面波处理带来的误差较小，故默认空间内的地震波均为平面波。当入射波遭遇地层阻抗变化时，分别产生折射P 波和SV 波、反射P 波和SV 波。假定入射P 波与入射SV 波的数量相等，且地震波总数为2n，其中n 为正整数。在入射地震波幅值方面，假设入射波幅值满足区间（0，1）的均匀分布，在获得地震运动场后通过控制点运动峰值对运动场的幅值进行调整。由于缺少入射波波形研究资料，将入射波的波形均假定为地震模拟中常用的Ricker 子波。在地震波入射角方面，假设P 波和SV 波入射角在一定范围内均匀分布，通过地震波的不同入射角组合获得空间差异地震动场。

2.3 非一致运动场的表达受半无限介质自由面边界条件限制，P 波与SV 波倾斜入射到自由面时，通常均会产生反射P 波与反射SV 波两类波型。以AP、AS分别代表入射P 波对应反射P 波、反射SV 波的幅值系数，以BP、BS分别代表入射SV 波对应反射P 波、反射SV 波的幅值系数。依据自由面边界条件得到的反射波幅值系数可表示为：

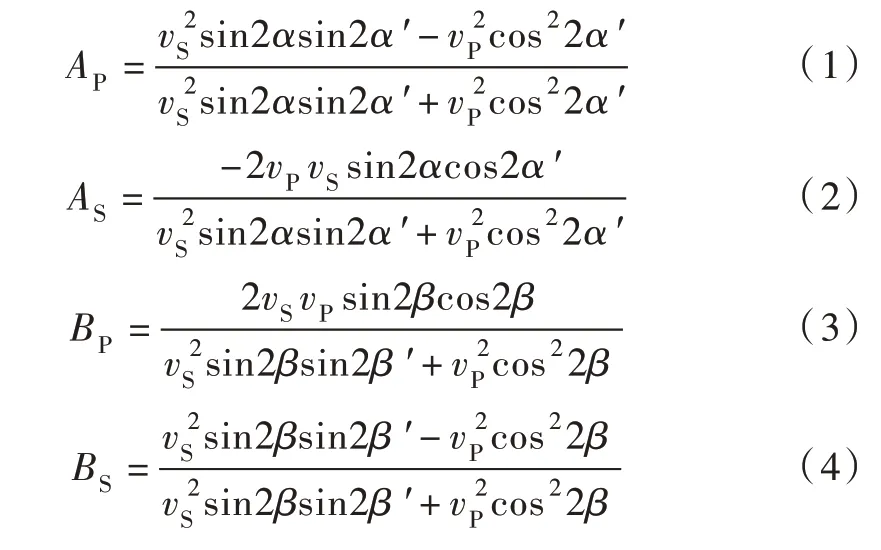
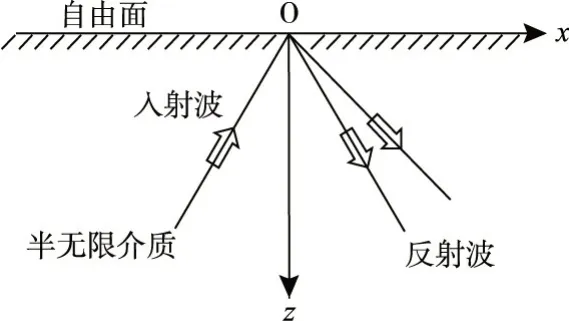
图1 半无限介质坐标系

式中：α、α′分别为P 波入射角及其产生的反射SV 波反射角； β、 β ′分别为SV 波入射角及其产生的反射P 波反射角；vP、vS分别为介质中P 波和SV 波波速，由半无限介质的拉梅常数确定。

确定输入地震动或地震动场时，须首先选定控制点。在半无限介质内建立如图1所示坐标系，并选择坐标原点O（0，0）作为控制点。入射平面P 波的波函数可表示为：

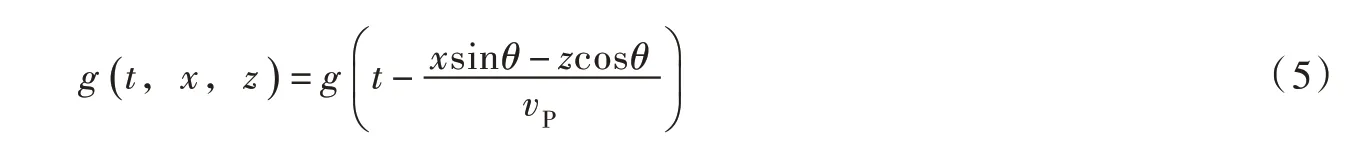
入射P 波对应反射P 波和反射SV 波的波函数可分别表示为：

入射SV 波的波函数可表示为：

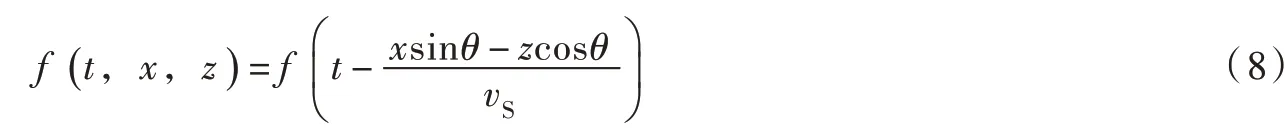
入射SV 波对应反射P 波和反射SV 波的波函数可分别表示为：

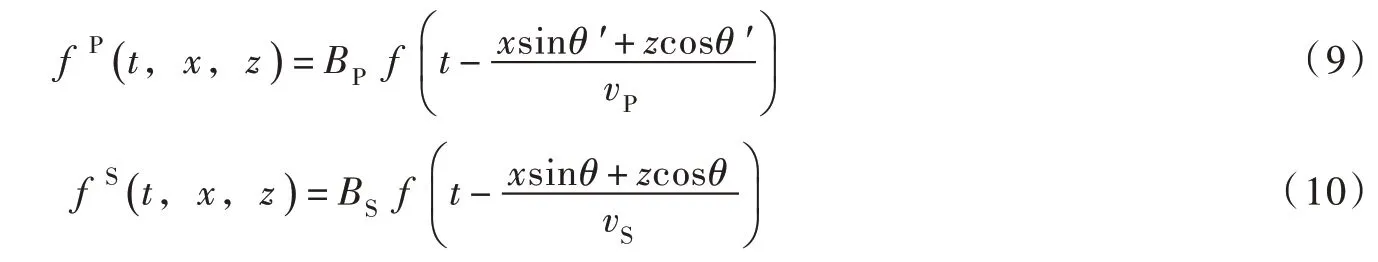
将半无限介质内存在的所有入射波、反射波运动场的叠加称为总运动场，任意质点运动的水平分量和竖直分量可表示为：

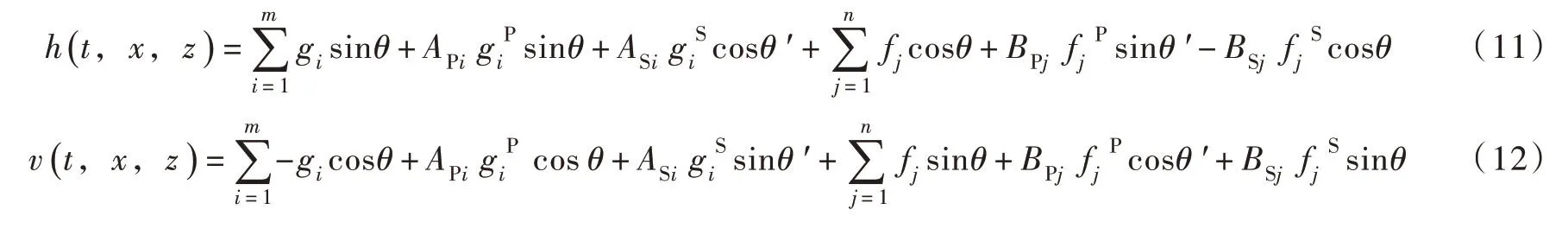
式中：h、v 分别为质点运动的水平和竖直分量；m 为入射P 波的数量；n 为入射SV 波的数量；i 为入射P 波及其反射波的编号；j 为入射SV 波及其反射波的编号；APi、ASi分别为入射P 波对应反射P 波、反射SV 波的幅值系数；BPj、BSj分别为入射SV 波对应反射P 波、反射SV 波的幅值系数。

对外源波动问题，入射波信息是空间差异地震动场和结构地震响应的直接影响因素，因此在结构地震响应分析中，对入射波运动场的描述是重要工作。忽略反射波项，得到入射波运动场的水平和竖直分量为：

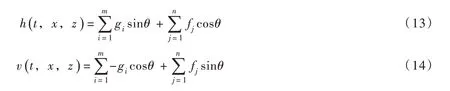
3 研究方案和地震动空间差异

3.1 研究方案前文在波动输入模型基础上，结合地震波组合效应提出确定非一致地震动场模型。为研究地震动场的确定性空间差异对结构地震响应的影响，分别以确定非一致地震动场和波动输入模型对应地震动场为基础，以重力坝为例，研究确定性地震动空间差异对结构地震响应的影响。

制定两种研究方案：方案1 通过确定非一致地震动场模型获得复杂入射地震波形成的空间差异地震动场，以非一致地震动场作为输入获得重力坝地震响应，称为确定性差异方案；方案2 以确定非一致地震动场模型获得的控制点运动作为已知地震动，结合垂直入射假设获得对应入射波运动场，作为输入获得重力坝地震响应，称为垂直入射方案。为保证方案间的可比性，将确定非一致地震动场在控制点的水平向运动峰值加速度均调整为1 m/s2。

3.2 地震动场空间差异两种方案对应的半无限介质参数取为弹性模量15 GPa、泊松比0.2、密度2400 kg/m3。入射波的基本波形选取主频2 Hz 的Ricker 子波，加速度时程如图2所示。由于基本波形较为简单，须增加入射波数量以保证得到的质点运动与实际地震动的相似性，入射波数量定为256，其中P 波和SV 波的数量分别为128。

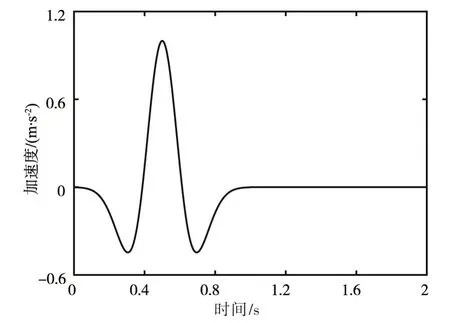
图2 基本波形Ricker 子波

地震学研究成果显示，地震波传播到场址附近时以小角度入射的可能性更大。将P 波和SV 波的入射角度组合取为表1的9 种工况，每种工况执行10 次获得入射地震波信息及其对应地震运动场。表1列出了9 种工况总运动场和入射波运动场在控制点的水平和竖直向运动的峰值平均值。依据地震波运动特征，P 波入射角度的增加带来运动水平分量的增大和竖直分量的减小，SV 波入射度的增加引起水平分量的减小和竖直分量的增大。从总运动场竖直向峰值与水平向峰值的比值可看出，依据确定非一致地震动场模型得到的控制点运动峰值平均值反映出该特征。由于运动场由复杂入射地震波引起，入射波引起的控制点运动与总场控制点运动的峰值不再满足折半关系。

表1 地震波入射角方案组合及控制点两向运动峰值比

分别选取控制点及其两侧2 km 位置共3 个特征点展示确定非一致地震动场质点运动的空间差异。图3和图4分别为工况1 的第1 次计算获得的水平向和竖直向运动。从图3、图4可看出，由于地震波在空间内的组合效应更符合实际地震动场的形成过程，基于确定非一致地震动模型获得的不同质点运动不仅包含运动的时间滞后，也包含幅值变化和质点运动时程形状的差异。

图3 工况1 第1 次计算特征点水平向加速度

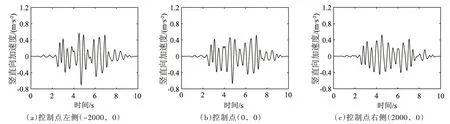
图4 工况1 第1 次计算特征点竖直向加速度

图5、图6分别显示了9 种工况下，自由面上加速度水平向和竖直向正峰值的空间分布，图中给出每种工况前5 次计算对应运动场。与垂直入射自由面运动峰值保持一致不同，采用确定非一致地震动场模型得到的自由面水平向和竖直向运动峰值均随空间位置变化，由于每次执行程序所生成的组合入射地震波存在差异，因此地震动场的空间差异表现出不同规律。

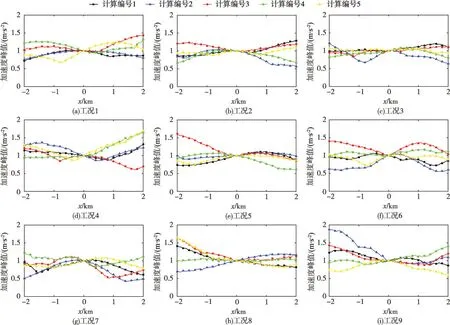
图5 自由面水平向加速度峰值空间变化

综上，确定非一致地震动场模型通过引入地震波组合效应使地震动场在保留波动输入模型优势的同时，可考虑空间质点运动的复杂幅值变化和时程形状变化等。在地震动空间差异的宏观特征方面，确定非一致地震动模型与实测地震记录更为接近［3］。

4 重力坝-地基有限元模型及地震动输入方法

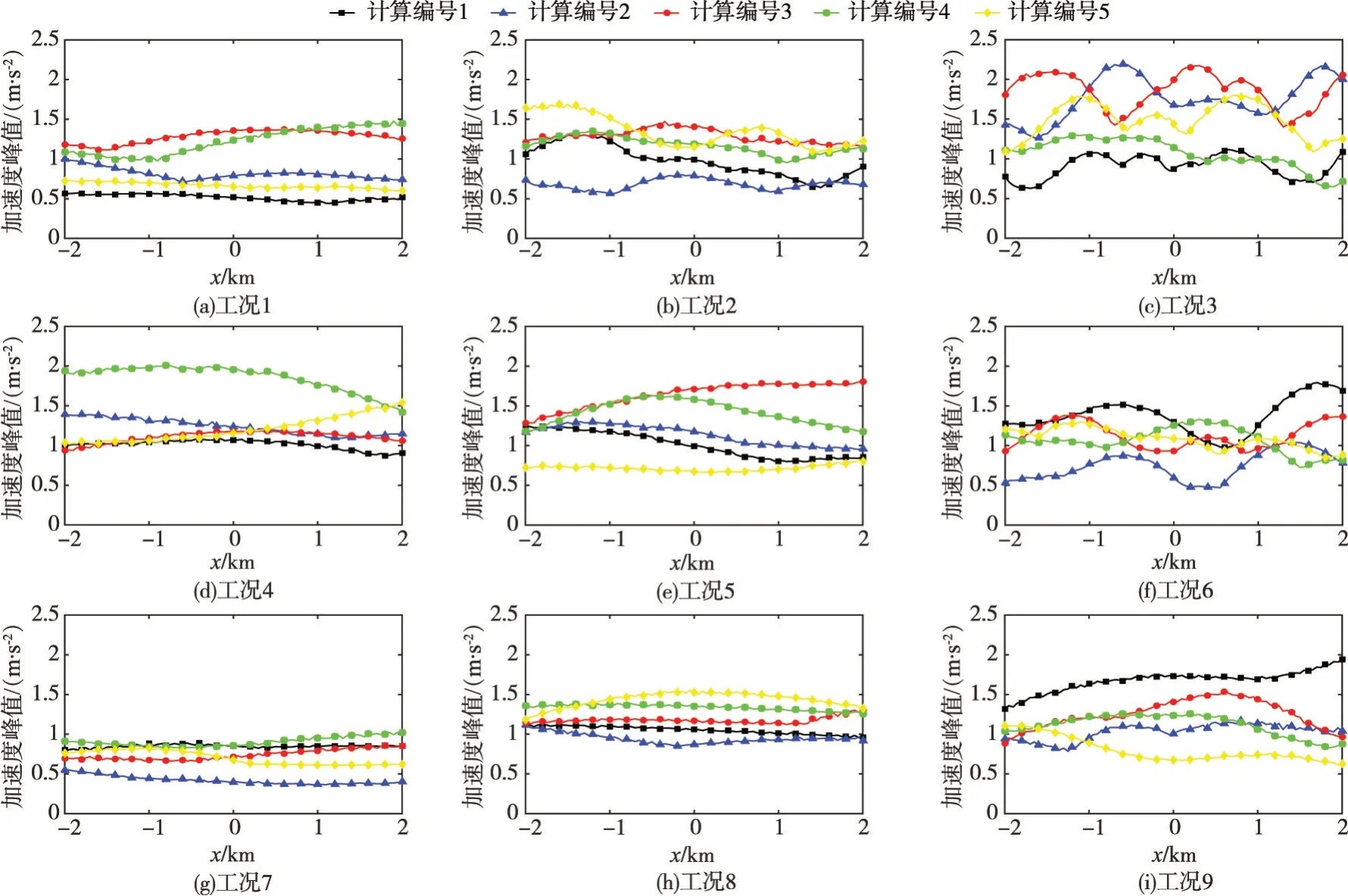
图6 自由面竖直向加速度峰值空间变化

4.1 重力坝-地基有限元模型以坝高150 m 的非溢流重力坝坝段为例研究确定性地震动空间差异对重力坝地震响应的影响。坝体采用平面应力单元模拟，坝基采用平面应变单元模拟，地基范围在上、下游和底部均取为300 m，坝体有限元网格如图7所示。

坝体和坝基计算参数见表2，坝体动态弹性模量取为静态弹性模量的1.5 倍。采用Rayleigh 阻尼模型，依据阻尼比0.1 和模型前两阶自振频率确定阻尼系数［25］。

表2 材料参数

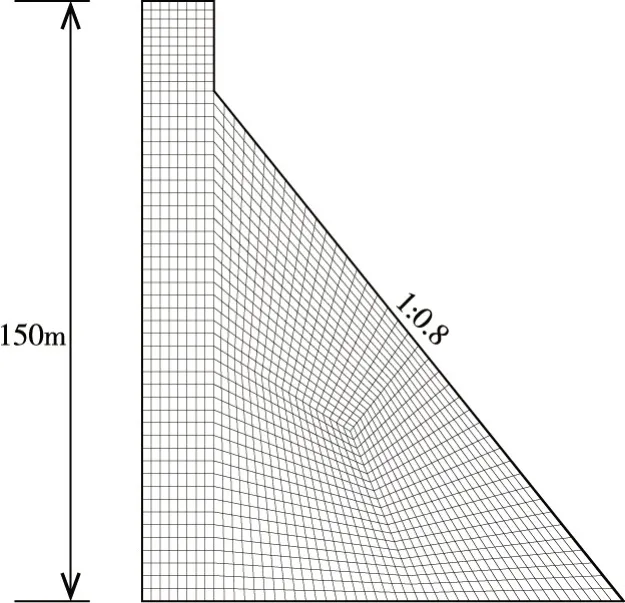
图7 坝体有限元模型

计算中考虑坝体自重、上游面水压力、扬压力、地震荷载和动水压力。动水压力采用Westguarrd附加质量表示，计算公式为：

式中：i 为坝体上游面节点编号；mi为坝体上游面节点对应附加质量；ρ为水体密度，取为1000 kg/m3；Ai为坝体上游面节点面积；yi为坝体上游面节点对应深度；H0为上游库水水深，取为150 m。

4.2 空间差异地震动的输入入射波运动场具有空间差异性，地震动输入须采用非一致输入方法。目前非一致地震动输入方法主要有加速度输入法、位移输入法、大质量法和大刚度法等。考虑到大坝地震响应分析通常以加速度为基础，采用大质量法实现重力坝地震响应分析的非一致输入。大质量法通过在边界节点附加一个较大的质量，将节点加速度时程转化为边界节点力完成非一致输入，其平衡方程可表示为：

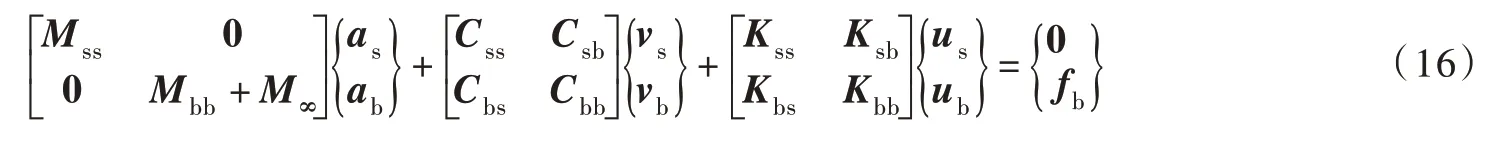
式中：M、C、K 分别为质量、阻尼和刚度矩阵；a、v、u 分别为加速度、速度和位移向量；s、b 分别为结构和边界节点自由度；fb为地震在边界节点引起的作用力；M∞为在边界节点附加的大质量，计算中附加质量取为结构总质量的108倍。

由于附加了大质量，边界节点上的作用力fb可近似表示为：

两种研究方案中，确定性差异方案的边界节点运动场由复杂入射波运动叠加形成；垂直入射方案的边界节点运动由垂直入射地震波形成。

5 确定性地震动空间差异对重力坝地震响应影响

考虑到地震响应计算耗费较高，将每种工况的计算样本数量定为10 次，通过样本计算结果反映确定性地震动空间差异的影响。重力坝的坝踵、下游面折坡处和上游面区域是抗震薄弱部位，选取坝踵和下游折坡处在静、动荷载作用下的主拉应力峰值进行计算。

表3列出9个工况下坝踵和下游折坡主拉应力峰值的平均值。从表3可看出，确定性地震动空间差异通常会引起重力坝坝踵、下游折坡处主拉应力峰值平均值的增加。坝踵主拉应力峰值平均值在工况2 增幅最大，由5.55 MPa 增加到6.95 MPa，增幅25.3%；下游折坡主拉应力峰值平均值在工况8 增幅最大，由1.88 MPa 增加到2.76 MPa，增幅46.4%。相对来说，下游折坡处的主拉应力峰值平均值的增幅比坝踵更大。

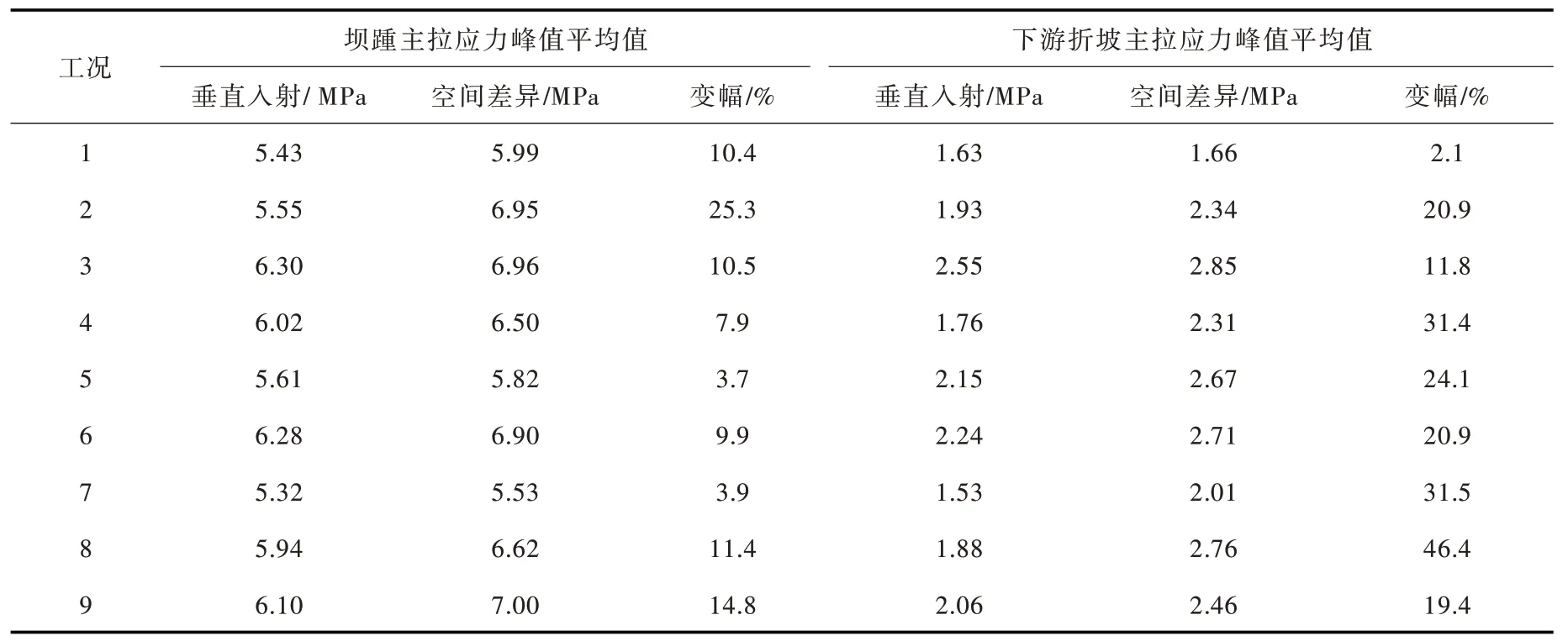
表3 各工况坝踵和下游折坡主拉应力峰值平均值对比

考察单个计算方案的坝踵和下游折坡主拉应力响应峰值，确定性地震动空间差异可能引起响应的增加或减小，坝踵主拉应力峰值增加的计算次数为58 次，占比64.4%；下游折坡主拉应力峰值增加的计算次数为69 次，占比76.7%。图8为两种计算方案坝踵主拉应力峰值对比。从图8可以看出，确定性地震动空间差异引起坝踵主拉应力最大变幅为：工况9计算编号2，坝踵主拉应力峰值由4.01 MPa增加到7.75 MPa，增幅93.1%；工况6 计算编号4，坝踵主拉应力峰值由6.35 MPa 减小到3.95 MPa，降幅37.8%。可看出，受到确定性地震动场考虑运动复杂幅值变化和时程形状差异的影响，重力坝的地震响应可能产生增加或减小，但增加的计算次数占比更大，且主应力峰值的最大增幅远大于最大降幅。

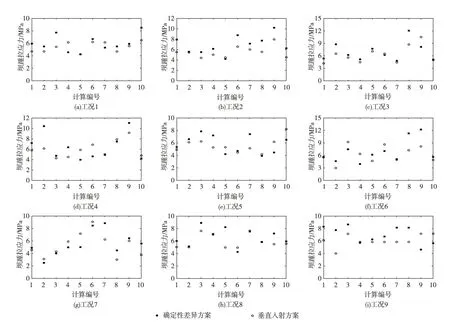
图8 确定性差异与垂直入射方案坝踵主拉应力结果对比

以坝踵拉应力峰值为准，将工况9 计算编号2 称为增幅算例，工况6 计算编号4 称为降幅算例。图9为增幅算例和降幅算例重力坝的主拉应力峰值包络图。从图9可以看出，在增幅算例中，确定性地震动空间差异引起坝踵、坝体上游面、下游折坡区域高拉应力范围的增大；在降幅算例中，确定性地震动空间差异引起坝踵、坝体上游面高拉应力范围的减小，但在下游折坡区域引起高拉应力范围的增大。

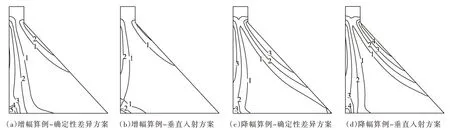
图9 增幅算例和降幅算例坝体主拉应力峰值包络图

图10为两种计算方案中坝踵和下游折坡主拉应力时程曲线。从图10可看出，在增幅算例中，确定性空间差异均引起了坝踵和下游折坡主拉应力峰值的增大；在降幅算例中，确定性空间差异引起了坝踵主拉应力峰值的降低，但引起了下游折坡主拉应力峰值的略微增加。

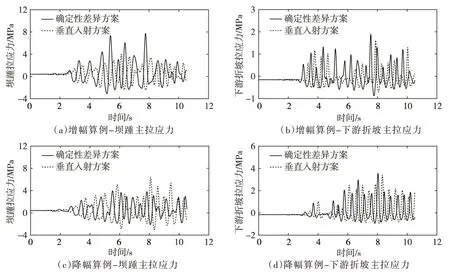
图10 坝踵和下游折坡主拉应力时程

6 结论和讨论

针对高坝-地基体系地震响应分析对空间差异地震动场的需求，总结目前地震工程学中地震动输入模型和强震地震动场的研究现状。通过分析已有地震动场构建方法的优势和缺陷，以准确表达地震动的空间差异和便于工程应用为目标，在波动输入模型基础上引入地震波组合效应，提出确定非一致地震动场模型。模型以随机生成的复杂入射地震波反映地震波从震源传播到场址的复杂化过程，以地震波组合效应描述地震动的确定性空间差异。在地震动场方面，确定非一致地震动场模型可在保留波动输入模型优点的同时，更全面地考虑不同空间点多维运动的时间滞后、复杂幅值变化和时程形状差异。相对于波动输入模型的地震动场，确定非一致地震动场在地震动空间差异的宏观特征上与实测地震记录更吻合。

重力坝地震响应的统计结果显示，与垂直入射空间差异地震动场相比，确定性地震动空间差异使重力坝坝踵和下游折坡处的主拉应力峰值平均值增加，本文计算工况中坝踵和下游折坡处的最大增幅分别达到25.3%和46.4%。重力坝坝踵拉应力响应峰值增加的计算次数占比例为66.4%；下游折坡拉应力响应峰值增加的计算次数占比例为76.7%。当考虑确定性地震动空间差异时，重力坝地震响应规律更加复杂。当确定性地震动空间差异引起地震响应增加时，通常会带来坝踵、坝体上游面和下游折坡等抗震薄弱部位拉应力范围的增加和数值的增大；当确定性地震动空间差异引起个别部位响应降低时，也有可能引起其他部位响应的增加。综合分析，确定性地震动空间差异在下游折坡处引起的主拉应力峰值平均值增幅较大，说明在全面考虑地震动空间差异时，结构在下游折坡处更易破坏。出于安全考虑，高坝-地基体系的非一致地震响应分析不能仅考虑行波效应，也须考虑幅值变化、时程形状差异等确定性空间差异的影响。

确定非一致地震动场模型的关键在于入射地震波信息的描述，场址入射地震波信息依赖于地震学研究成果的支撑。由于目前地震学研究在场址入射地震波信息方面的成果较少，本文暂时采用随机模型描述入射地震波信息。随着地震学相关研究的推进，对入射地震波信息描述准确性的增加可使确定非一致地震动场对实际地震动场具有更好的代表性。考虑到确定非一致地震动场模型以波动输入模型为基础，通过引入地震波组合效应对地震动场空间差异进行描述，在对比分析部分主要与波动输入进行对比，与其他输入方法进行对比是进一步的研究工作。在地震动空间差异描述方面，实际地震动场所包含的空间差异并不局限于确定性部分，也包含随机性部分。在确定非一致地震动场模型基础上考虑随机因素的影响，是可继续推进的研究方向。在地震动空间差异对结构地震响应影响方面，本文暂以重力坝线弹性响应开展分析，研究地震动确定性空间差异对重力坝非线性地震响应和破坏模式的影响，并与实际重力坝地震震损案例进行对比，是验证模型的下一步工作。