分层流体中冰脊拖曳力的数值模拟研究
祖永恒,卢 鹏,王庆凯,李志军,吴 岩,李 博
(大连理工大学 港口海岸及近海工程国家重点实验室,辽宁 大连 116024)
1 研究背景
流体分层是自然界普遍存在的一种现象,包括大气分层和水体分层。流体分层主要受其温度和密度的控制,在以密度为主导的分层环境中,物体在流体中的相对运动会呈现出不同于均匀流的动力特性。例如,河口附近由于海水和淡水的密度差异会形成一个切变锋面,锋面上层是淡水层,下层是海水层,这对通行的船舶以及寒区河冰的运动都有重要影响[1-3]。冰盖或冰塞等对上层流体的扰动会在流体分界面激起内波,内波同时又会改变冰盖或冰塞受到的拖曳力,从而进一步影响冰塞的堆积演变。王军等研究了均匀流体条件下直槽中冰塞的形成机理,并给出了试验条件下不同冰塞形成机制的临界弗劳德数Frc范围在0.12~0.13[4]。寒区水库解冻初期的水温分布差异也会引起表层的浮力流动现象,对水库的冰情、下泄水温造成影响[5]。李嘉等使用二维水库水温模型分析了水库的分层流场和温度场的耦合规律[6];郑铁钢等采用量纲分析方法研究了水温分层对水库下泄水温的影响[7]。但是寒区水库中冰凌冰塞的产生也会改变分层流体的水动力情况,进而也会对水库下游取水的水温、水质造成影响,针对这方面的相关研究有待深入。
海洋中的流体分层现象也较为普遍,特别是近年来北极夏季海冰加速融化,导致海洋盐跃层变浅甚至在海冰边缘区和冰脊深度达到同一量级,此时海冰运动激发界面内波将会对冰脊拖曳力造成不可忽略的影响[8-10],甚至发生死水现象[11]。根据海冰拖曳系数参数化的思想,冰-水总拖曳力包括摩拖曳力和形拖曳力两部分。其中,摩拖曳力描述的是由海冰表面均匀分布的小凸起物引起的剪切力,形拖曳力描述的是由海冰表面非均匀分布的较大凸起物(如冰侧、冰脊)引起的流场变化而导致的水平方向压力差[12],不同类型的冰面粗糙物由截断高度来划分[13]。冰脊形拖曳力对冰-水总拖曳系数的贡献可由下式定义:

式中:A 为冰密集度;hk/Lr为冰脊密度;即冰脊的入水深度hk和冰脊间距Lr之比;Cr为单个冰脊的局地拖曳系数。若A 和hk/Lr一定,Cr直接决定了冰脊对冰-水界面拖曳系数的贡献。在冰脊分布密度较大时,冰脊形拖曳力对冰-水总拖曳系数的贡献不可忽略[14]。因此,研究单个冰脊局地拖曳系数的变化规律对于冰-水界面的动量交换研究具有重要意义。
真实的流体分层存在连续分层和多层等复杂情况,可以采用双层流体对该问题进行简化。双层流体的物理实验具有较强可操作性,可以精确再现流体分层情况,并反映出不同流态下分层流体的变化特征。Pite 利用该方法对冰脊拖曳力问题进行了研究,并结合Baines 对内波流场的描述,根据内弗劳德数(无量纲拖曳速度)和冰脊入水深度的变化,将双层流流况分为亚临界区、跨临界区(下风波区)和超临界区[15-16]。Jammel 利用基于欧拉方程的有限差分算法对Pite 的分层流体实验进行了数值模拟[17];Mortikov 利用浸没边界法对双层流体的边界进行了更精细化的处理[18]。这些研究多是对双层流产生的内波和内波拖曳力进行定性分析,并未建立双层流中冰脊形态和冰-水拖曳系数的参数化关系;而且已有数值模拟研究中很少考虑湍流模型的应用,对冰脊后的流场压强也缺少分析。随着计算流体力学的发展,通过并行计算已经大大提高了湍流模型的计算效率。本文采用基于有限体积法的RNG k-ε湍流模型和VOF 界面追踪方法对该问题进行数值模拟研究。通过对数值模拟流场的处理,与物理实验的结果进行了对比,分析了动压强对内波增阻的影响,揭示了冰脊局地拖曳系数随着冰脊入水深度和流场弗劳德数变化的一般规律。
2 分层流试验研究
数值模拟计算域的设置与先期进行的实验室物理实验在垂向尺寸上完全一致。物理实验是在大连理工大学海岸及近海工程国家重点实验室的粒子图像测速水槽完成(见图1),该实验的详细论述见文献[19]。水槽长450 cm,宽23 cm,深45 cm,上层淡水深15 cm,下层盐水深20 cm。冰脊模型的材料为有机玻璃,冰脊底角设计为45°。拖车由电机牵引在水槽上方的轨道上运行,可带动冰脊以1、3、6、7、8、9、10、12、15、18、24、30 cm/s 等不同的速度在水槽内匀速运动。冰脊入水深度可调,实验设置了4、6、8、10 cm 4 种入水深度。冰脊模型在水平方向上连接拉压传感器,再固定在拖车上,能够测量模型在水平方向受到的流体拖曳力。

图1 物理实验水槽
水槽中产生的内波最大传播速度不会超过其相速度。本研究中的内波相速度约为14 cm/s,因此数值模拟中计算域长度分别向上下游延长实际水槽长度的一倍,数值计算时间不超过40 s 以消除侧边界反射的影响。对于流体的物理参数,数值模拟和物理实验的取值保持一致,淡水的密度为998.2 kg/m3,动力黏性系数为1.0003×10-3kg/(m·s);海水的密度为1025 kg/m3,动力黏性系数为1.12×10-3kg/(m·s)。考虑到在水槽宽度方向上流速变化较小,将数值模拟简化为二维问题,冰脊以恒定的速度和入水深度在水面处沿水平方向运动,流体初始速度为0,和物理实验的组次一致,见图2。

图2 数值模拟水槽示意图(单位:cm)
本研究模拟双层流中内波的产生,遵循重力相似准则。空气、上层流体密度差与上下层流体的密度差的比值为(ρ1-ρa)/(ρ2-ρ1)≈37,产生的表面波的波高和内波的波高之比也为1/37,因此表面波的影响忽略不计[20]。弗劳德数Fr 是重力相似准则中判定流况动力相似的无量纲参数,定义为冰脊拖曳速度和线性内波相速度的比值:

式中:V 为冰脊拖曳速度;C 为线性内波相速度。模型比尺应满足:

内波相速度采用线性非色散的长波相速度[18]:

式中ρ0、h0为模型中的特征密度和特征深度。Pite 统计的现场观测数据显示,当冰脊运动速度在0.2 m/s、入水深度为10 m 时,弗劳德数的变化范围是0.12 ~0.69,冰脊入水深度和上层流体深度之比的变化范围是0.12 ~1.38;但在后来的观测资料中,弗劳德数的变化范围可以达到0.2 ~3.8[16,22]。数值模拟和物理实验中弗劳德数的变化范围是0.07 ~2.14,冰脊入水深度和上层流体深度之比的变化范围是0.27 ~0.67,保证了本研究结果能够覆盖现场不同的内波形态,包括亚临界区、跨临界区和超临界区。
在数值模拟的计算域中(见图2),上边界DK 为压强入口,入口压强为0(参考压力为大气压);外边界DG、GH、HK 都为壁面,速度为0;其中冰脊ABC 也是壁面,同时也是运动的内边界,运动速度为冰脊的拖曳速度。
计算域用三角形网格和四边形网格进行构建。图3是网格划分示意图,其中冰脊附近的区域为三角形非结构网格,其他区域是四边形结构网格。包含冰脊部分的网格设定为动网格,冰脊边界以恒定速度向左运动,下方为静止网格。动网格区域和静网格区域通过一对interface 界面实现数据交换。

表1 网格无关性验证结果
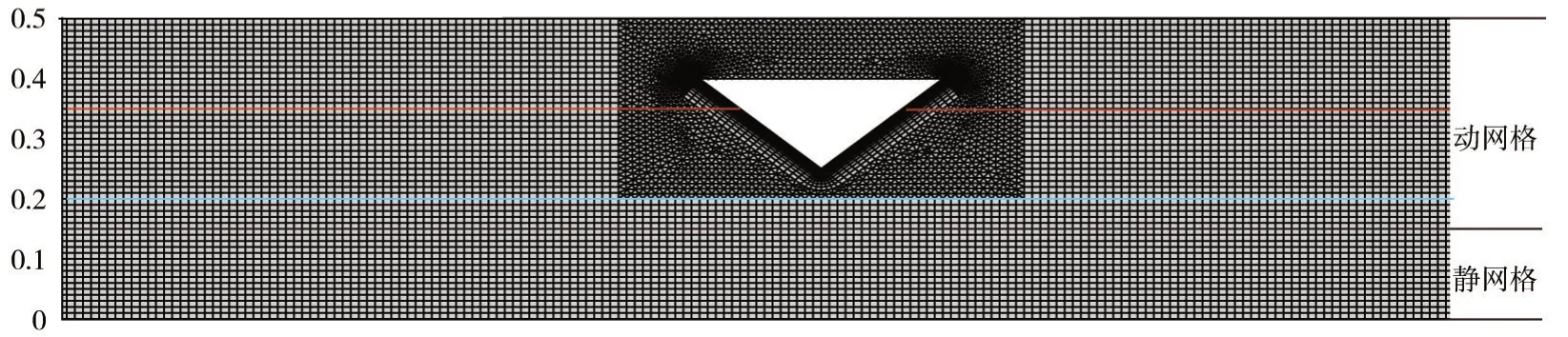
图3 网格划分示意图(红色为水-气界面,蓝色为密度分界面)
数值模拟中的冰脊入水深度最大为10 cm,非结构网格也最复杂,故网格大小的无关性验证选取T=10 cm、V=15 cm/s 组次,检验结果见表1。当网格步长为0.8 cm ~1.2 cm 时,计算结果已趋于稳定,相对误差不超过3%。故选取空间步长1 cm。
流场计算的控制方程采用基于雷诺应力平均方程的RNG k-ε湍流模型,k-ε两方程如下:
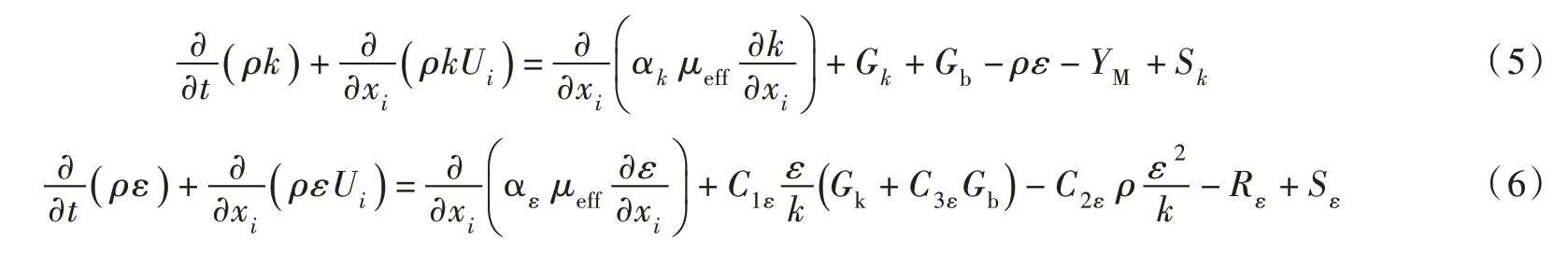
在Fluent 软件中,Cμ=0.0845,C1ε=1.42,C2ε=1.68,αε=αk=1.39。控制方程在时间离散方式上采用一阶隐式离散,空间离散方式上采用二阶迎风离散。求解算法是在SIMPLE 算法(压力耦合方程组半隐式方法)基础上修正的PISO 算法(隐式算子分割算法)。冰脊的运动采用动网格模块,使用铺层(layering)方案进行求解。对于界面的追踪,选用基于Youngs 算法Geo-Reconstruct 方案计算网格边界的流体体积量。
3 计算结果和分析
为了方便分析,引入无量纲参数B,定义为冰脊入水深度T和上层流体深度h1的比值:

对于单个冰脊的局地拖曳系数Cr,采用阻力系数的定义形式:

式中:F 为冰脊受到的流场拖曳力;ρ1为上层流体密度;A 为冰脊在垂直于运行方向的投影面积;V为冰脊的运动速度。
3.1 冰脊拖曳力随速度的变化冰脊拖曳力F 由冰脊表面应力(包括黏性应力和压强应力)在水平方向上的积分得到,F 随冰脊运动速度V 的变化情况以及与物理实验结果的对比如图4所示。

图4 数值模拟冰脊拖曳力和物理实验对比结果

图5 数值模拟拖曳系数随弗劳德数的变化和物理实验的对比结果
由图4可以看出来,数值模拟和物理实验在Fr<1 时均表现出了非线性,拖曳力随速度的增加先增大后减小。当Fr>1 时,拖曳力随着速度的增大而增大。这一现象在拖曳系数的变化规律中更加明显,而且当Fr>1 后,拖曳系数趋近于1,和单层流拖曳系数的变化规律相似,见图5中数值模拟和物理实验的对比结果。
在图5(b)中,物理实验得到的拖曳系数的非线性变化并不明显,这是由于物理实验条件的限制造成的。当速度为1 cm/s 时,物理实验中的拖曳力值甚至不到10-3N,由力值计算得到的拖曳力系数也会产生误差,导致了物理实验在小速度区间的拖曳系数变化规律不太明显,但此时数值模拟中拖曳系数的非线性变化则较为显著。当Fr<1 时,拖曳系数随速度先增大后减小,峰值随着入水深度的变化而变化。当Fr>1 后,拖曳系数不再随速度的变化而变化,而是趋近于单层流体的冰脊拖曳系数。
需要注意的是,图4中的数值模拟的冰脊拖曳力结果相比物理实验存在一定差异,主要是由两种方法中流体密度剖面的差异造成的,密度剖面的差异导致了浮频率N 的变化,见图6数值模拟中流体分层条件和物理实验的对比。在流体分界面,数值模拟可以直接定义一个密度断面,断面上浮频率趋近于无限大。但物理实验需要在一个深度区间内完成密度的连续变化,即在约7 cm 的区间内由淡水过渡到盐水,图6(b)物理实验中的浮频率最高达到3 rad/s。
对于密度线性变化的连续分层流体,当h=35 cm 时,其内波相速度C:

而本研究采用两层流体线性假设下的内波相速度C:
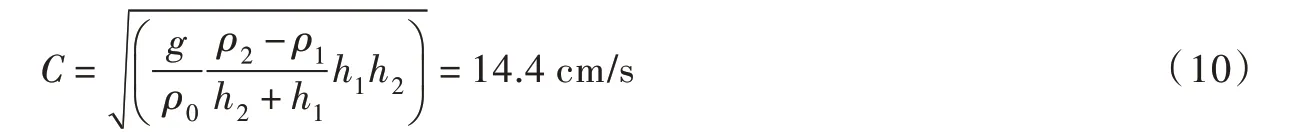
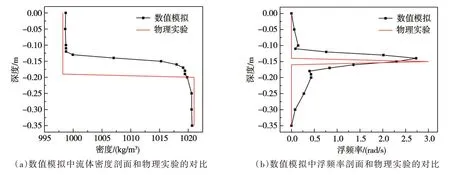
图6 数值模拟中流体分层条件和物理实验的对比
由上面两式可知相速度C 和密度梯度相关,数值模拟中分界面的密度梯度大于物理实验值;而物理实验中在分界面附近属于连续分层,在整体上又属于双层流情况,因此物理实验的内波最大相速度应小于数模,介于8.1 cm/s 和14.4 cm/s 之间,并偏于14.4 cm/s。所以图4中物理实验拖曳力的非线性区间比数值模拟值提前,该区间拖曳力的峰值也比后者提前,造成了数值模拟和物理实验出现差异。
当Fr>1 时,双层流中冰脊拖曳力受内波影响较小,内波拖曳力几乎为零,拖曳力的变化规律和单层相似,此时数值模拟和物理实验吻合良好。单层流冰脊拖曳力数据可以参考吴岩等人的研究成果[23]。另外,图7(a)给出了冰脊入水深度T=8 cm 时,在双层流中的拖曳力与在单层流中拖曳力数值模拟结果的对比,从图中可以看出相同水深情况下,双层流的阻力情况相对单层流复杂一些。以Fr=1为分界点,前面区间的阻力差异较大,这是由于内波的生成,对冰脊后的压力场产生了较大的影响,本文后面章节还会详细分析。当Fr>1 后,内波对冰脊阻力的影响几乎可以忽略了,单、双层流中冰脊拖曳系数都在1 左右,见图7(b)。

图7 T=8 cm 时,数值模拟的冰脊拖曳力和拖曳系数在单层和双层流中的变化结果
3.2 冰脊拖曳力随入水深度的变化双层流中冰脊拖曳力、拖曳系数随无量纲入水深度B 的变化规律见图8所示。
当Fr 一定时,拖曳力随着入水深度的增加而增大,接近于线性变化。从拖曳系数来看,当Fr>0.57 时,拖曳系数的变化较小,接近于1,如图8中Fr=0.86、Fr=1.07、Fr=2.14 时的情形。当Fr≤0.57 时,拖曳系数随着入水深度的增加而显著增大,而且拖曳速度越小,拖曳系数变化幅度越大,如图8中Fr=0.42、Fr=0.57 的情形。
由拖曳系数的定义可知,拖曳系数和冰脊运动速度的平方呈反比。因此当速度较小的时候,拖曳系数对拖曳力的变化更加敏感。拖曳力的非线性变化出现在弗劳德数较小的区间,此时拖曳系数随Fr 的变化趋势更为显著(图7)。因此图8中Fr 较小时拖曳系数的变化幅度要大于Fr 较大时的变化幅度。
3.3 内波形态的变化规律图9给出了入水深度T=6 cm,速度V=15 cm/s 时冰脊运动对应的典型内波形态。在拖曳系数随Fr 变化的非线性区间,内波波速大于冰脊的运动速度,因此内波的扰动可以向上下游同时传播。此时内波向下游传播到一定的距离便完全耗散,而内波波谷向上游延伸,并且波面变化幅度较小,近似平缓的曲线。在下游形成的内波比较稳定,波峰相对冰脊的位置都保持不变。
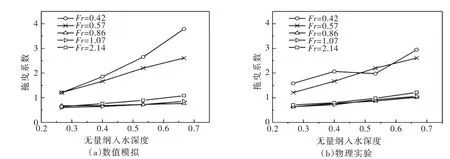
图8 冰脊拖曳系数随无量纲入水深度的变化结果
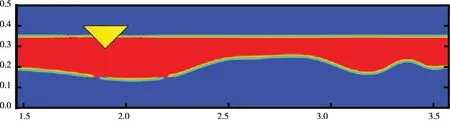
图9 冰脊入水深度T=6 cm,速度V=15 cm/s 数值模拟的内波

图10 数值模拟内波无量纲化波高和物理实验对比结果

图11 冰脊入水深度T=8 cm,速度V=7 cm/s 数值模拟内波形态和物理实验的对比结果(黑色虚线为初始分界面)
随着弗劳德数的增长,冰脊上游的扰动消失,仅冰脊下方出现波谷状态。此时,下游内波仍处于比较稳定的状态。而当Fr>1 时,由于冰脊的拖曳速度超过了内波的相速度,内波扰动仅向冰脊下游传播,而且第一个波峰逐渐变得平坦,并逐渐远离冰脊。当Fr=2.1(V=30 cm/s)时,内波形态变得更加杂乱,波峰不断远离冰脊,最终扰动逐渐消失,流态过渡到超临界区域。
其他入水深度条件下产生的内波形态和T=6 cm 的情形一样,但波峰高度有所不同。为进行数值模拟和物理实验的比较,把内波最低点与最高点的高度差定义为内波波高H,H/h1为无量纲化波高,图10是不同入水深度情况下无量纲波高的对比。
图10中数值模拟的波高比物理实验结果偏大,但趋势一致。在跨临界状态,波高随着速度的增大而增大;在超过临界状态后,波高开始趋于平稳。数值模拟与物理实验的差异还是由于上文中提到的密度分层的不同,它导致了图11中物理实验的掺混现象比较明显,消耗了更多的能量。而数值模拟中的波形则比较稳定,因此内波波高相对较大。
3.4 内波对冰脊拖曳力的影响由图7中的对比可知,在拖曳力变化的非线性区间,内波对冰脊拖曳力产生了重要影响,下面从垂直于冰脊运行方向和平行于冰脊运行方向两个方面对该问题进行分析。首先对于垂直方向,统计了非线性区间的流体界面垂直偏移的最大值D,该距离随弗劳德数的变化规律见图12。从图中可知,偏移距离D 和拖曳力F 在跨临界区域相关性较高,相关系数R2>0.94。分界面位移的变化可以反映出流体势能的变化,同时,由于上层流体通道束窄,流速也会增加。同一流线在该位置势能增加,动能增加,而且下层流体对上层流体的剪切力做负功,流线的压强势能则会降低,在分界面位移最高处形成一个相对低压区。
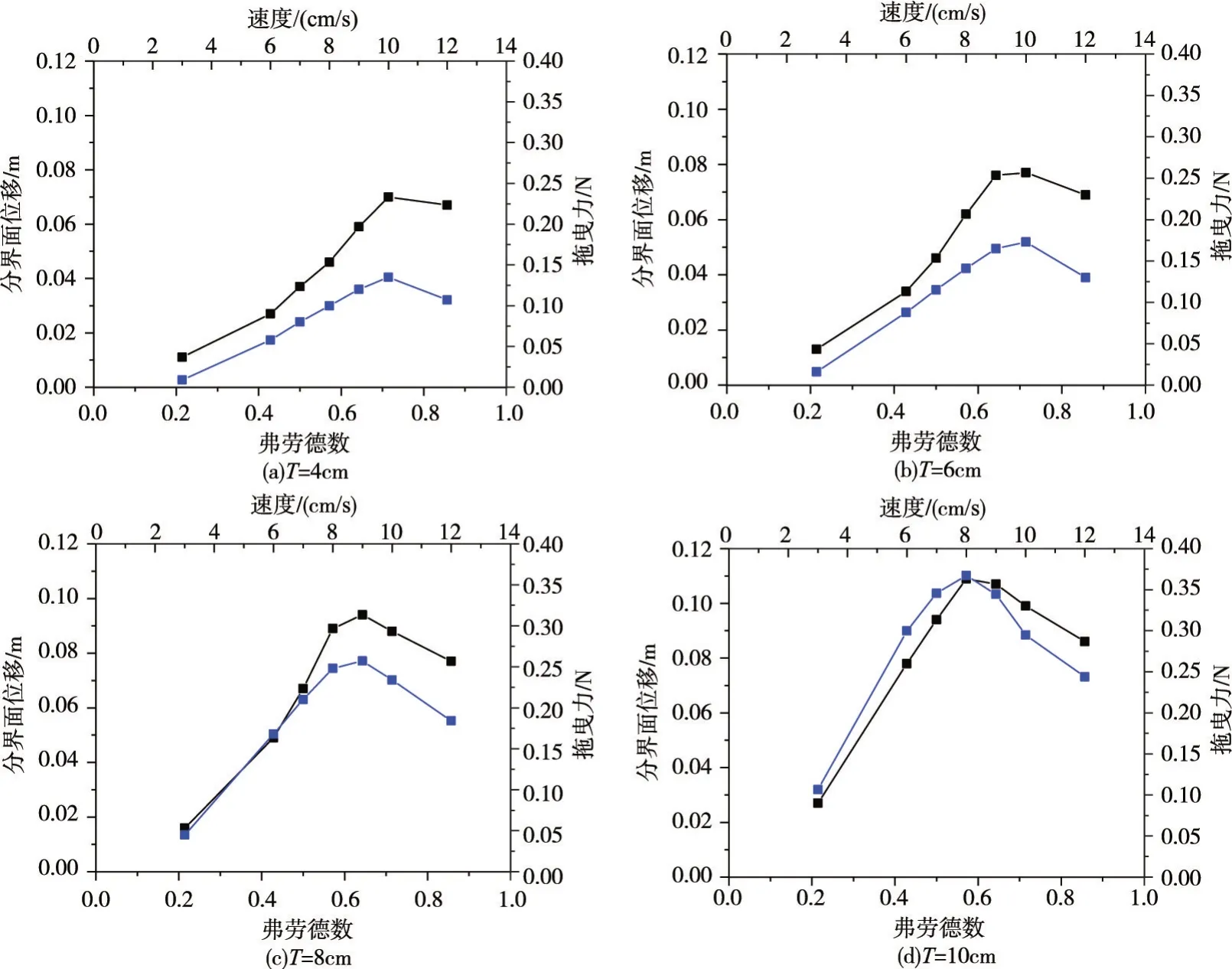
图12 数值模拟分界面位移和冰脊拖曳力关联图(蓝线是拖曳力,黑线是位移)
对于平行冰脊运动方向,冰脊拖曳力主要是由冰脊前后压强场的变化引起的。因此对冰脊附近的压强场进行后处理,将流场总压强减去静压,得到流场的动压强。这样更容易反映出冰脊前后压强的变化,结果见图13。
图13是不同运动速度冰脊附近的压强场和流场。可以看到双层流体中不仅会在冰脊后形成一个尾流漩涡场(和单层相同),而且还会在内波扰动的波峰、波谷处形成漩涡场。每一个漩涡场都是一个相对低压区,涡动中心的压强最低,这也是冰脊产生拖曳力的原因。在单层流中,冰脊拖曳力只是受尾流漩涡场一个低压区的影响,而且随着速度的增大,漩涡中心的相对压强降低。然而在双层流中,冰脊拖曳力要受尾流漩涡场和冰脊后第一个内波波峰漩涡场的双重影响。尤其当拖曳速度小于内波相速度时,内波扰动向冰脊上下游同时传播,此时内波的形态相对冰脊比较稳定,跟随冰脊的运动而运动。波峰的漩涡场和尾流漩涡场共同作用,对冰脊拖曳力产生影响。
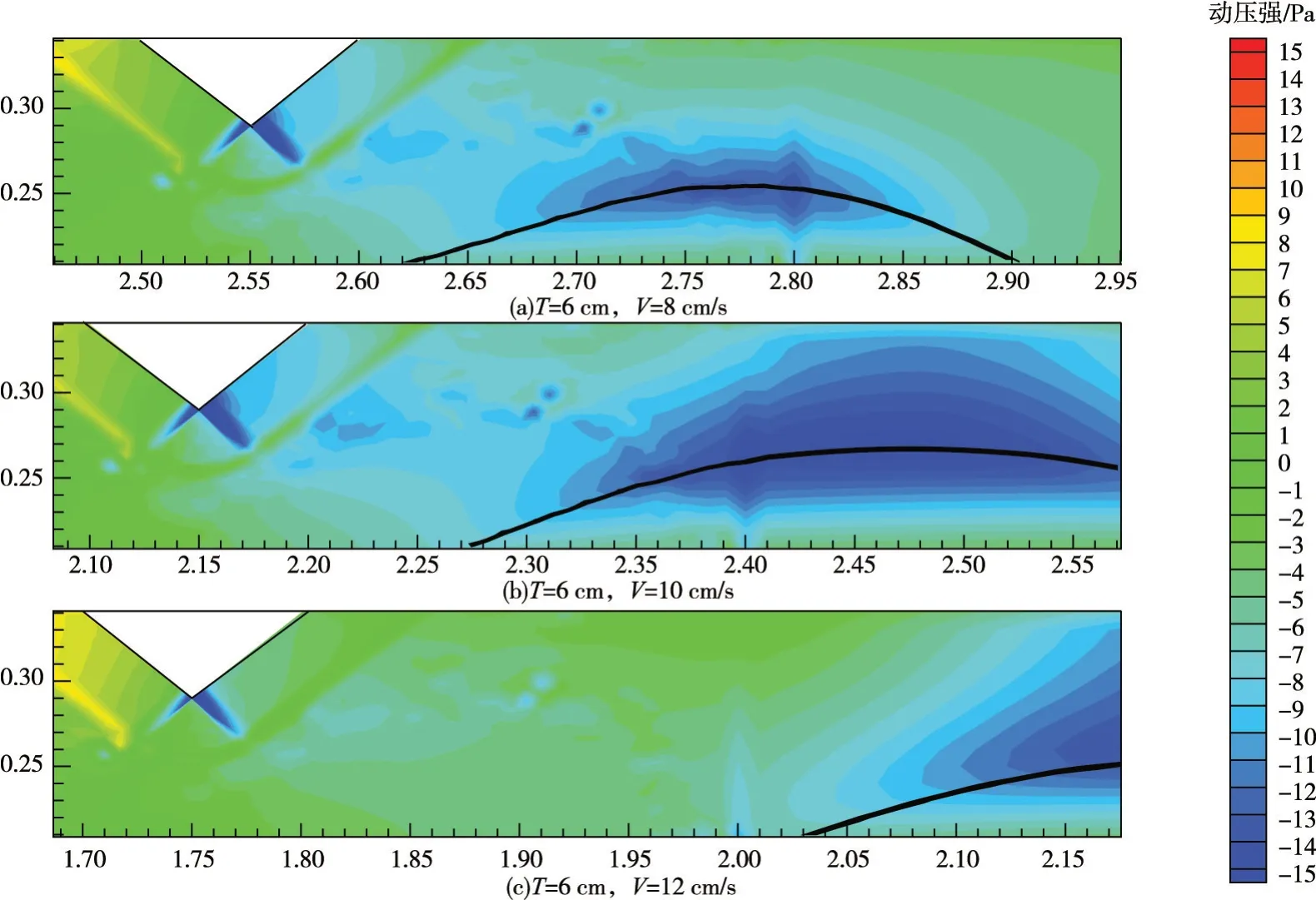
图13 数值模拟分层流体冰脊附近动压强分布云图(黑色实线为内波波面)
随着速度的增大,图13中内波波峰不断远离冰脊,对冰脊尾流场的影响也越来越小,冰脊拖曳力也逐渐趋近于单层流的情况。在Fr=0.71(V=10 cm/s)时,内波波峰的漩涡区对冰脊尾流的漩涡区影响最大,内波波峰的高度也达到最高(图12(b))。此时尾流漩涡区不能充分发展,受到内波波峰漩涡的“挤压”效果,漩涡的相对压强也最低,因此出现了冰脊拖曳力的极值。其他入水深度条件的冰脊拖曳力变化规律和T=6 cm 的情况类似。
4 冰脊底角的影响
除了流速和入水深度会对冰脊的拖曳力产生影响外,冰脊形状也会造成一定的差异。利用数值模拟可以探究冰脊拖曳力随着不同冰脊形状或者分层水深的变化规律,但由于篇幅限制,只给出冰脊形状变化的定性结果。
由图14可知,当冰脊底角在30°到60°范围内,拖曳力的变化规律基本相似。相同速度和入水深度下,拖曳力角度的增大而变大。冰脊拖曳系数随着角度的增加而增加,在非线性区间向线性区间的转换过程中,拖曳系数随角度的变化稍微平缓,见图15中Fr=0.71 的情况,其他弗劳德数区间的变化趋势基本一致。内波形态的演变对冰脊底角的变化并不敏感,主要还是受弗劳德数的影响。

图14 T=6 cm,不同冰脊底角的拖曳力随弗劳德数的变化

图15 T=6 cm,拖曳系数随角度的变化:Fr≤0.71 为非线性区间、Fr>0.71 为单调区间
5 结论
双层流环境下冰脊拖曳力随着冰脊运动速度和冰脊入水深度的变化而变化,对应的冰脊拖曳系数受弗劳德数和冰脊的无量纲入水深度的影响。数值模拟得到的冰脊拖曳力和拖曳系数与物理实验结果基本吻合,在跨临界区域内都表现出冰脊拖曳力和拖曳系数的非线性变化规律。数值模拟产生的内波形状和物理实验结果一致,但由于分界面密度分布的差异,物理实验中存在更多的掺混现象,消耗了更多的内波能量。
当入水深度保持不变时,冰脊拖曳力随着拖曳速度的增加有先增加后减小、然后再增加的趋势。冰脊拖曳系数随弗劳德数变化的规律更加明显,非线性变化峰值出现的位置也较拖曳力提前。当弗劳德数Fr>1 时,双层流的冰脊局地拖曳系数稳定于1,与单层流的冰脊局地拖曳系数差异不大。对非线性区间分界面位移和冰脊附近压强场的分析发现,当位移达到最大时,拖曳力达到一个峰值。而且内波波峰和流场压强相互耦合,随着分界面垂直偏移距离的增加,内波波峰附近的负压区域增大,在波峰位置不随时间变化的情形下,会影响冰脊后的尾流负压区,使拖曳力出现峰值。当冰脊运动速度保持不变时,在Fr≤0.57 的较小范围内,冰脊拖曳系数随入水深度的增加而增加;在Fr>0.57 的较大范围内,冰脊拖曳系数基本不随入水深度的增加而变化,最终趋近于1。
单个冰脊的局地拖曳系数对冰-水总拖曳系数的确定具有重要作用,结合流体分层的物理实验研究,本文利用数值模拟方法探讨了双层流中冰脊拖曳系数随冰脊入水深度和弗劳德数变化关系,为分层流体冰-水拖曳系数的参数化奠定了基础。除了冰脊入水深度和运动速度,冰脊形态和分层水深的变化也会对冰脊局地拖曳系数产生影响,需要进一步的试验研究和理论分析,从而发展完整的冰脊拖曳系数参数化方案。

