自吸泵内能量损失及非定常流动特性研究

舒 欣，任 芸，吴登昊，祝之兵，牟介刚

（浙江工业大学 之江学院，浙江 绍兴 312030；2.浙江工业大学 机械工程学院，浙江 杭州 310014）

1 研究背景

自吸泵由于其具备良好的自吸性能，而被广泛地应用于农业灌溉、市政排水、食品和印染等行业［1］。由于自吸泵具有气液分离腔、回流孔等特殊结构，气液分离腔内部存在明显的扩散和冲击损失，同时运行过程中回流孔处回流液体使得其内部的水力损失明显高于普通离心泵。因此，其水力效率普遍偏低。为此，深入研究自吸泵内能量损失特性具有重要的科学意义。

由于离心泵几何结构的复杂性和不对称性，使得其内部流动具有显著的非定常特征，流动分离［2］、二次流［3］、动静干涉［4］、失速［5］及各种尺度的漩涡现象加剧了离心泵内部的能量损失。因此，不少学者研究了泵内部不稳定流动结构（比如，失速团或者漩涡）与其水力损失的关联。随着计算流体动力学的发展，离心泵内部的瞬态流动特性以及流动损失机理得到了进一步的揭示。Zhang 等［6］采用DDES 方法对离心泵内部的非定常射流-尾迹流动结构及其演化特征进行了深入分析，揭示了叶片尾迹是引起离心泵内部局部漩涡和压力波动的主要原因。Zhou 等［7］采用大涡模拟方法分析了离心泵内部失速涡的演变规律，揭示了随着叶轮内部失速涡的发展，其内部流动损失和压力波动的强度得到了显著增长。同时，在非设计工况下，离心泵内部的流动状态变得十分的不稳定，极易诱发强烈的漩涡，进而导致离心泵内部产生显著的能量损失［8-9］。如果能够定量地揭示离心泵内不同区域的能量损失大小及分布规律，就可以针对性地去优化离心泵的水力设计参数以改善其性能。

熵产代表了一个系统的不可逆性及流动中能量损失的大小，近年来，该理论在离心泵能量损失评估方面得到了一定的发展。大量研究表明，熵产理论与传统的水力损失评估法相比，其优势在于能够准确地预测离心泵内能量损失的具体区域，直观地反映泵内能量损失的分布特征，为研究人员的后续改进优化提供准确直观的参考信息［10-13］。张永学等［14］利用局部熵产方法对离心泵内的能量损失特性进行了系统评估，揭示了叶轮和蜗壳是熵产发生的主要区域。王松岭等［15］利用熵产理论对优化前后离心风机的损失特性进行研究，揭示了优化后风机的效率提高了0.5%。张帆等［16］采用熵产的流动损失分析方法对侧流道泵内的流动损失的分布特征进行分析，提出了侧流道泵内部流动损失主要与湍流流动增加的熵产有关，叶轮流道和侧流道内的湍动耗散率远大于直接耗散率。卢金玲等［17］采用熵产理论对水轮机尾水管内的涡带特征及压力脉动特性进行了研究，发现水轮机的叶片压力面的流动分离是熵产产生的主要原因，涡带的产生使得尾水管区域出现高熵产率的带状区域。同样，熵产理论也被用于分析多级离心泵［18］以及自吸泵［19］内部的能量损失特性。

鉴于自吸泵的特殊结构，气液分离腔及回流孔的存在使得其内部流动更加复杂，目前关于自吸泵内的流动损失研究还不充分，对流动损失出现的具体位置及损失机理的研究也较少。本文拟采用熵产理论对不同工况下自吸泵内的能量损失特性进行系统研究，定量分析自吸泵内不同区域的能量损失特点，为自吸泵的优化设计提供一定的理论基础。

2 熵产理论

熵产理论是一种不可逆的过程，机械能的损失会转换成内能，这是不可逆的，最终会引起熵产的增加。根据第二热力学定理，在实际的流体系统中也存在熵产。因此，为了更加有效地解释泵内流动损失现象，这里采用熵产理论来对泵内能量损失进行解释。

通常，离心泵内的流动是一种湍流状态，对于湍流而言，熵产有两个部分：一部分是由时均运动引起的；另一部分则由瞬态的速度波动引起的。因此，熵产率（Entropy Production Rate，EPR）可以采用以下公式进行表达［20］：

由时均和脉动引起的熵产如式（2）和式（3）：

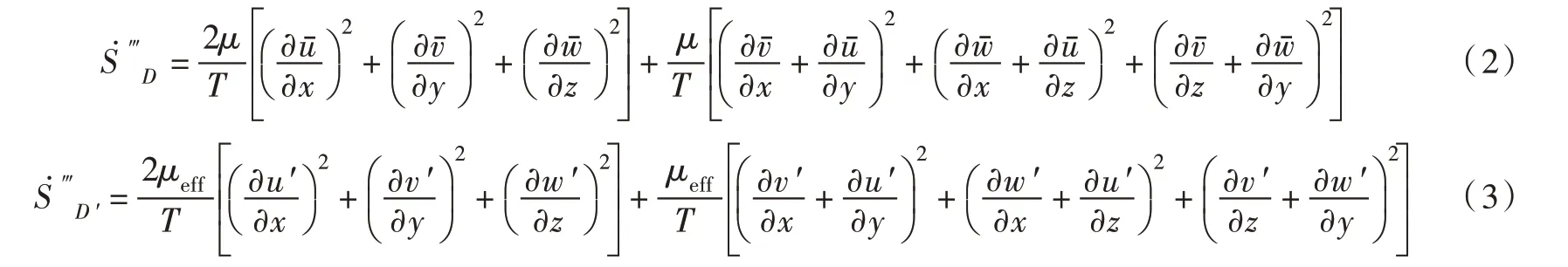
式中μt为湍流运动黏度。

式中：α=0.09，ω为湍流涡频率，s-1；k 为湍流强度，m2/s2。

然而，由于熵产率存在较强的壁面效应，且时均项较为明显，其壁面附近熵产计算的公式为：

式中：为壁面切应力，Pa；S 为面积，m2；为近壁面速度，m/s。

因此，整个系统计算域内的总熵产计算公式为：

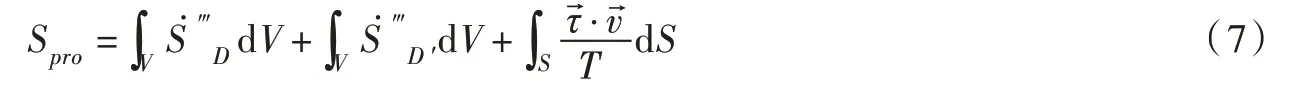
3 数值计算

3.1 计算对象本文以比转速为231 的自吸泵模型作为数值研究对象，该模型为外混式双叶片自吸泵，其主要设计参数如表1所示，计算流体域如图1所示。在建模过程中，除了主要的叶轮、蜗壳、气液分离腔、吸入段和进出口延长管外，还考虑了回流孔、口环的间隙以及叶轮的前、后盖板腔体，以便更加准确的对实际模型进行表达。计算域白色虚线的位置为两个流体域之间的交接面。

表1 模型泵设计参数

图1 数值计算流体域

3.2 计算网格和湍流模型采用GridPro 软件对模型进行结构化网格划分，如图2所示。通常，在计算时网格数越多，计算误差会越小，同时计算时又要兼顾计算的时间性，因此开展了网格无关性分析，以确定适合的网格数。网格无关性分析如图3所示，从图3可以发现，当网格数达到300 万左右的时候，设计工况下的扬程和扭矩基本保持稳定，其中扬程值H 稳定在16.7 m 左右，扭矩值T 稳定在19.4 N·m 左右；当网格数达到440 万时，总熵产值Spro稳定在3.7 W/K 左右。因此，为了兼顾计算精度和计算时间，最终模型的总网格数定为440 万，其中叶轮、蜗壳、气液分离腔、吸入段的网格数分别为68 万、46 万、215 万、17 万，其他计算域为94 万。由于叶片壁面存在较高的压力和速度梯度，需要对叶片近壁面的网格进行局部加密，使得第一层网格布置保证y+≤30，满足了应用标准壁面函数对近壁面区的流动特征进行求解的计算要求［22］。表2为设计工况下的湍流模型无关性验证结果，可以看出不同湍流模型对计算结果的影响较小，相对误差基本控制在3%之内，满足相关计算精确要求。相比k-ε湍流模型，SST k-ω［21］湍流模型是一种双方程的涡黏性模型，其利用壁面函数能够比较精确地获取叶轮机械近壁面区低雷诺数的黏性特征，而且在带有压力梯度的流动中其计算结果更加准确；同时，该模型相比大涡模拟方法，其所占用的计算资源更加合理，更适用于工程应用。因此，本项目最终选择SST k-ω作为后续计算的湍流模型。同时，由于本文只针对自吸泵输送液体介质时的水力损失及其非定常特性，并未涉及自吸过程的气液两相流动特征，因此，计算中只考虑了单一介质，并未考虑自吸泵的气液两相流动特性。

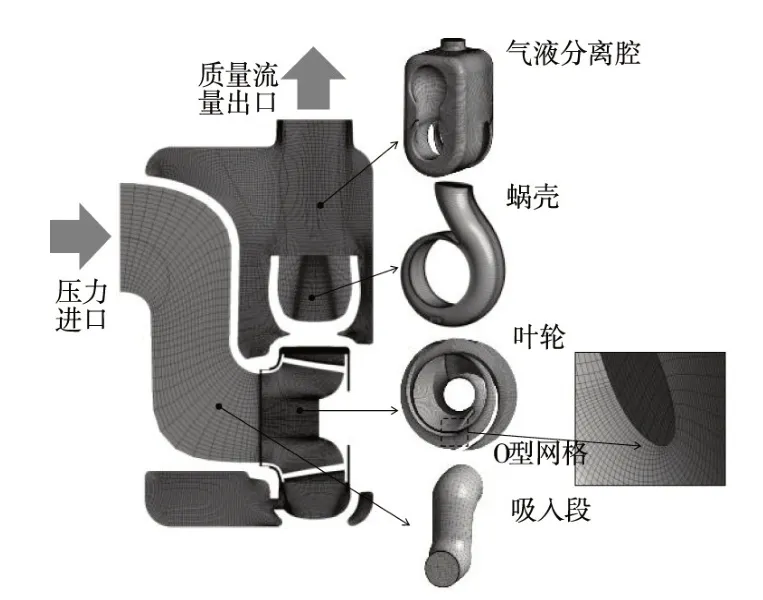
图2 计算网格

图3 网格无关性分析

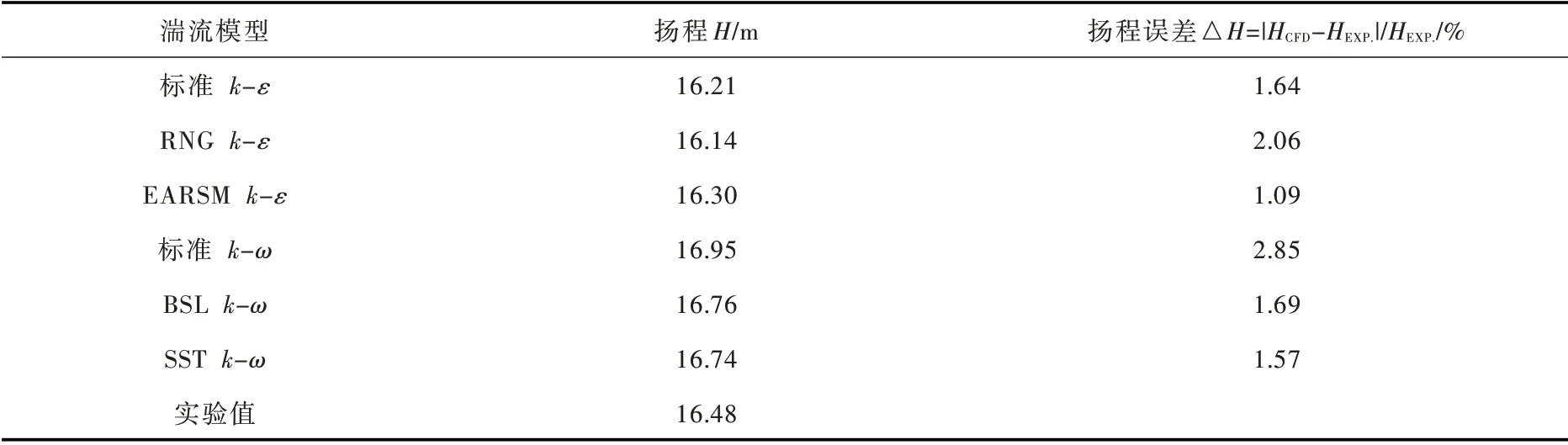
表2 湍流模型无关性验证（Q=1.0Qd）

3.3 边界条件及监测点分布计算时，在泵进口给定总压为0 Pa，同时出口设为质量流量出口。定常计算过程中，采用冻结转子法耦合动静部件，非定常计算中动静部件采用瞬态转子-定子法耦合，将定常计算结果作为非定常计算的初始条件，残差收敛精度为10-5，为了充分获取自吸泵内部压力脉动及径向力的非定常情况，设非定常数值模拟过程中物理时间步长为叶轮转动周期的1/120（每隔3°采集一次），即非定常物理时间步长为0.000 172 414 s，每个时间步长迭代20 次，采样时间为8 倍的叶轮旋转周期。固壁条件：固壁上满足无滑移条件，近壁区采用伸缩壁面函数处理；流体域的粗糙度平均设为0.04 mm。图4为自吸泵内部压力脉动监测点示意图，监测点m1—m11位于蜗壳内部，以监测叶轮与蜗壳动静干涉诱导的压力脉动信息。

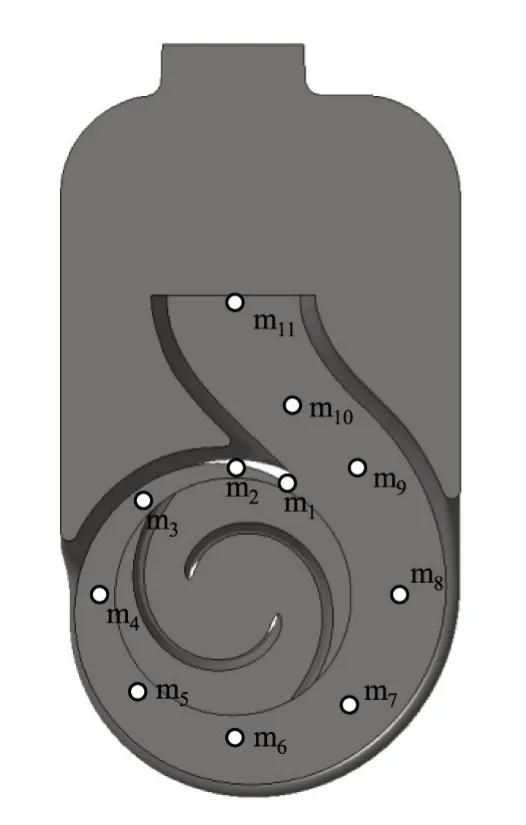
图4 压力脉动监测点

图5 模型泵性能实验

4 结果与分析

4.1 外特性对比分析通过闭式实验台对自吸泵模型的水力性能开展实验测量，如图5所示。图6为自吸泵非定常数值计算结果与实验测试结果对比数据，数值计算的效率考虑了机械损失和容积损失［1］。实验在闭式实验台上进行，实验流量误差为0.5%，压力测量误差为0.2%，转速测量误差为0.2%，扭矩测量误差为0.5%。可以发现：设计工况附近的扬程和效率误差均小于2%；非设计工况下的扬程误差有所增大，总体误差均小于5%。原因在于小流量工况下，泵内部的流动十分复杂，现有的计算模型很难对其进行十分精确的预测；同时在小流量工况下，实验测试的偏差也会较大，测试的压力和流量值会出现较大的波动，这些原因都会导致计算和测试出现一定的偏差。总体上说，数值计算结果与实验结果具有较好的一致性，精度基本满足后续计算和分析的要求。

图6 数值计算结果验证

4.2 泵内能量损失分布特征为了系统的分析自吸泵内流动损失分布特性，通过数值计算获取了不同工况下泵内部总损失扬程ht的计算见式（8）。

式中：hs为吸入段的水力损失，m；hi为叶轮的水力损失，m；hv为蜗壳的水力损失，m；hc为气液分离腔的水力损失，m。

图7 泵内能量损失分布规律

图7（a）为泵内水力损失分布特征，从图中可以得出：总水力损失为泵内4 个主要流体域内的损失之和，其值基本随着流量的增大，呈现先减小后增大的趋势；其中小流量工况下的损失值明显高于其他工况，设计流量工况附近的损失值达到最小。分析不同区域内的水力损失情况，可以看出叶轮和蜗壳是泵内水力损失的主要区域；吸入段和蜗壳内的水力损失从小流量0.3Qd下的4.67 m 和8.1 m，下降到设计流量工况1.0Qd下的0.13 m 和1.6 m；叶轮内的损失值在1.2Qd工况下达到最小；而气液分离腔内的水力损失分布特征则与其他区域存在明显的区别，其损失值基本上随着流量的增大而增大，并在大流量工况1.3Qd下达到最大值，其值为1.34 m，其主要原因在于气液分离腔内损失的主要形式为冲击和扩散损失，这两种损失主要取决于腔体内部的流速，通常流速越大，其对应的损失越大，故随着流量的增大，腔体内部的流速逐渐增大，进而引起更多的损失。

图7（b）为泵内不同区域的熵产分布规律，从图中可以得出：泵内总熵产值Spro在设计工况附近达到最小，其值为3.72 W/K；小流量工况下的总熵产值明显高于其他工况，0.3Qd下的总熵产值为11.25 W/K；总熵产值在不同流量下的分布规律与图7（a）中反映的泵内总水力损失（ht）的分布规律基本一致。分析不同区域内的熵产分布情况，得到叶轮和蜗壳内的总熵产值在小流量到设计流量区域明显高于其他区域，随着流量的进一步加大，气液分离腔内部的总熵产值逐渐高于其他区域；吸入段内的总熵产值主要体现在小流量工况，随着流量的加大，其内的总熵产值迅速降低并接近于零；个体区域的总熵产分布规律大致与图7（a）所反映的个体区域内的水力损失分布规律相似。

图8（a）为泵内不同区域的水力损失比率分布规律，从图中可以得出：叶轮和蜗壳是泵内水力损失的主要单元，其中叶轮内水力损失所占的比率基本维持在40%以上，最大的达到了57%；蜗壳内水力损失所占的比率基本维持在30%以上，最大的达到了43%；气液分离腔和吸入段内的水力损失所占比率偏小，其中气液分离腔在大流量工况下所占比率有所增加，最高达到24%；相反，对于吸入段，其在小流量工况下贡献较大，最高达到25%。从泵内主要区域的水力损失占比分布可以发现，叶轮和蜗壳是改善泵内水力特性的核心优化单元；而对于气液分离腔，其在设计过程中也需要给予一定的关注，因为在设计流量及大流量工况下，其所占的水力损失比重也较大。

图8 泵内不同区域的能量损失比率分布规律

图8（b）为泵内不同区域的总熵产比率分布规律，从图中可以得出：大部分工况下叶轮和蜗壳内的总熵产比率高于其他区域，其中叶轮内总熵产所占的比率基本维持在20%以上，最大的达到了61%；蜗壳内总熵产所占的比率基本维持在20%以上，最大的达到了41%；气液分离腔在大流量工况下所占的比率明显增大，最高达到44%；对于吸入段，其在小流量工况下贡献较大，最高达到14%。总的来说，泵内不同区域的总熵产比率分布规律与图8（a）中反映的泵内不同区域的水力损失比率分布规律基本一致。

4.3 泵内熵产分布特征以叶轮及整个计算流体域的中间截面作为分析对象，图9为不同工况下叶轮及泵内熵产对比分析图。

从图9中可以得出：（1）在小流量工况下，即0.5Qd，泵内的损失主要集中在叶片进口处和出口处，其主要原因在于：叶片进口处存在较严重的流动冲击（见图10中的1 号区域）及叶片压力面处的流动分离现象（见图10中的2 号区域）；在叶轮出口处存在大量的回流（见图10中的3 号区域），导致出口处易于形成大面积的漩涡；同时叶轮和隔舌的动静干涉效应进一步加剧了叶轮内部和隔舌附近的损失；（2）在设计流量1.0Qd工况下，叶轮内部的熵产值较小，泵内的损失主要集中在隔舌附近和蜗壳内，对比其他工况，设计工况下的熵产值最小，即其水力损失最小；（3）在大流量工况下，即1.2Qd，泵内的损失主要集中在隔舌、蜗壳以及气液分离腔内，在蜗壳出口处的气液分离腔中出现了较大的能量损失，其主要原因在于蜗壳内的液体以较高的流速进入气液分离腔，高速的流体与气液分离腔内低速的流体之间形成较大的剪切作用，进而形成较大的能量损失；同时高速的流体撞击气液分离腔内的壁面，进而形成较大的冲击损失。

图9 不同工况下泵内熵产分布特征

图10 小流量工况下叶轮内部速度场分布（0.5Qd）

4.4 泵内非定常流动特性为了分析不同工况下泵内压力脉动的特性，对11 个监测点的数据进行采集，记录一个时间周期内监测点m1—m11上的瞬态静压值。采用压力脉动强度μp作为衡量指标。计算公式如下：

图11为不同工况下蜗壳内部压力脉动强度分布情况，从图中可以看出，非设计工况下蜗壳内部的压力脉动强度在靠近隔舌区域较大，蜗壳中段处变弱，蜗壳出口扩散段处又进一步增强。该原因在于非设计工况下靠近隔舌区域会出现显著的动静干涉现象，局部区域的压力会随着叶片的旋转出现较大的波动；而对于出口扩散段，在大流量工况下，由于扩散段内流体易于产生局部的漩涡，因此，该工况下的压力波动明显高于其他工况。相比较而言，设计工况下蜗壳内部各点的压力脉动分布没有出现显著的差距，其仅在远离隔舌的蜗壳中段出现局部较低的压力脉动，其他区域基本相差不大。其原因在于设计工况下，蜗壳内部的压力分布相对比较均匀，叶片与蜗壳的动静干涉作用相对较弱。

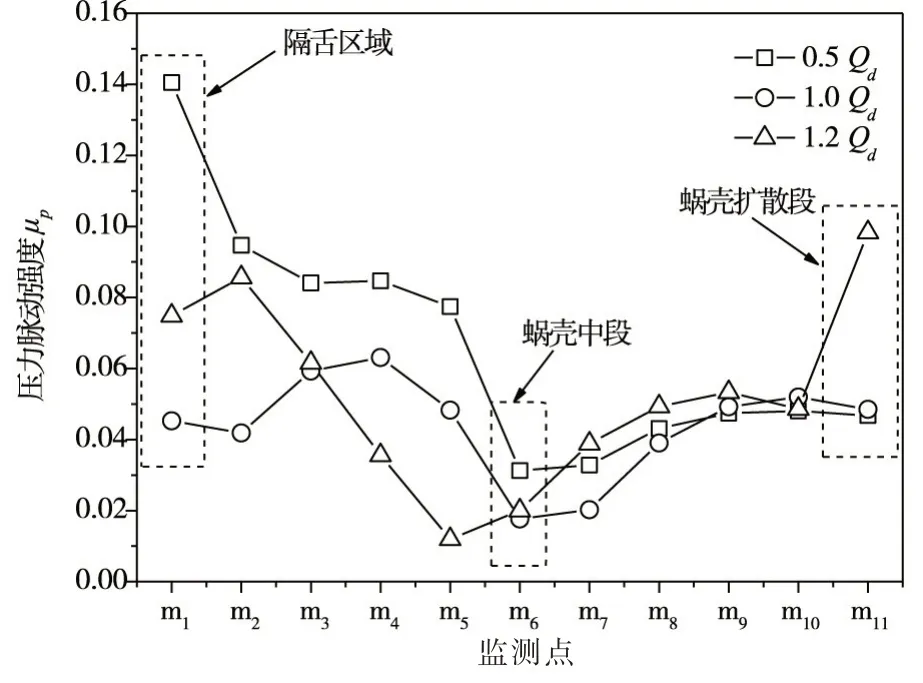
图11 蜗壳内部压力脉动强度分布规律

图12 不同工况下泵内涡核分布特征（t=0.146552s）

为了分析流量变化时，熵产、压力脉动与泵内流态之间的关系，需要识别泵内涡核的分布特征。这里选用物理意义明确的Q 准则［16］，Q=1/2（ΩijΩij- SijSij），式中：Ωij为旋转张量；Sij为应变率张量。当Q＞0 时，存在涡结构，Q 值越大，涡强度越大。Q 值的大小对涡识别具有较大的影响，随着Q 值的增加，所识别的涡结构逐渐减小；Q 值过大，只能识别少量的涡结构，会忽略许多有意义的涡结构，不利于分析；Q 值过小，则会出现大面积的涡结构，也不利于分析。综合分析不同Q 等值面下的涡结构分布特征，这里选择涡结构较为清晰的Q=1.5×105等值面来进一步研究不同工况下的涡结构特征。图12为不同工况下自吸泵内瞬态涡核分布特征。从图中可以看出：在小流量工况下，叶轮和蜗壳内部涡核分布面积较大，涡核主要分布在叶轮的进口处和出口处，出口的涡核主要分布在叶片压力面侧，而在叶片的吸力面其对应的涡核面积较小，该分布特征与图9（a）中反映的熵产特征较为一致，同时也解释了图11中反映的小流量工况下压力脉动强度较大的原因。小流量工况下，进口涡核产生的原因在于叶轮进口易出现液流冲击及流动分离，而叶轮出口处的回流及动静干涉现象是引起出口涡核的主要原因；在设计工况下，涡核分布面积显著减小；在大流量工况下，涡核的分布面积略微有所增加。3 种工况下，均在回流孔处出现涡核，其原因在于液体流经回流孔时存在局部收缩和扩张现象，进而导致不稳定涡的产生。

5 结论

本文采用熵产理论和Q 准则定量揭示了不同工况下自吸泵内能量损失特性和涡核分布特征，为自吸泵的优化设计提供了理论基础。主要研究结论如下：

（1）泵内熵产分布特征与水力损失分布特征基本一致，泵内总熵产值在设计工况附近达到最小，其值为3.72 W/K；小流量工况下的总熵产值明显高于其他工况，0.3Qd下的总熵产值为11.25 W/K；叶轮、蜗壳和气液分离腔是自吸泵内能量损失的主要区域，三者损失之和约为总损失值的90%。

（2）在小流量工况下，泵内的损失主要集中在叶轮内部进口处和出口处；在设计流量工况下，泵内的损失主要集中在隔舌附近和蜗壳内；在大流量工况下，泵内的损失主要集中在隔舌、蜗壳以及气液分离腔内。叶片进口处存在较严重的液流冲击及流动分离现象；在叶轮出口处存在大量的回流，导致出口处形成大面积的漩涡；同时叶轮和隔舌的动静干涉效应进一步加剧了叶轮内部和隔舌附近的损失；在大流量工况下，蜗壳内的液体以较高的流速进入气液分离腔，形成了较大的能量损失；同时高速的流体撞击气液分离腔内的壁面，引起了较大的冲击损失。

（3）小流量工况下，靠近隔舌区域会出现了强烈的动静干涉现象，局部压力出现了较大的波动；在大流量工况下，出口扩散段由于扩散段内流体易于产生局部的漩涡，该工况下的压力波动明显高于其他工况。涡核主要分布在叶轮的进口处、出口处，以及回流孔处，叶轮进口的流动冲击和叶轮出口处的回流及动静干涉是引起涡核的主要原因。

论文摘要编写要点

论文摘要十分重要，它是沟通读者和作者之间的桥梁。在今天信息时代，读者不可能阅读刊物的每一篇论文去查找所需的信息，只有通过摘要了解论文的主要内容，从而判断有无必要阅读全文。国内外的检索系统为了信息交流，更建立了各种二次文献数据库，帮助读者通过查找论文摘要，以便提取原文。而二次文献数据库的基础是作者的论文摘要。但许多作者却往往忽视了论文摘要的这一重要意义，没有下工夫把论文摘要写好，尤其是英文摘要。当今科技领域，英文已经成为国际交流语言，世界各国学者想追踪了解某一学科的发展情况，多会用英文工具书、数据库进行检索。而国外的检索系统也主要通过英文摘要判断论文是否被收录进数据库。为了帮助作者写好摘要，我编辑部在给作者的论文修改通知中都附有《摘要编写要点》，供作者参考。现再刊登于下，以便作者查阅。

1.摘要是论文内容不加注释和评论的简短陈述，应包括正文的要点，具有独立性和自含性，让读者不阅读全文就能了解论文的基本内容，以判断有无必要阅读全文，也可供二次文献采用。

2.摘要应说明研究工作的目的、方法与手段、结果和结论，要尽量简短，尽可能省略课题的背景信息。

3.摘要中的内容应在正文中出现，不能对正文进行补充和修改。

4.摘要中不用图、表、非公用共知的符号和术语，不能引用文献；缩写名称在第一次出现时要有全称（包括中文和英文）。

5.摘要中不要多列数据，出现的应该是最重要的、最关键数据。

6.中文摘要一般300 字左右，中英文摘要应基本对照，不能因为某些内容不好翻译就略去。

7.关键词是为了文献标引工作，是从论文中选取出来用以表示全文主题内容信息的单词或术语，一般为3～8 个词，尽量用规范词。

《水利学报》编辑部