粉质黏土中筒型基础沉放的影响范围研究
刘 润,李贝贝,马文冠,练继建,陈广思
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
1 研究背景
风能作为一种无污染的清洁能源逐渐引起人们的重视,由于陆上可开发的风电资源有限,近些年来全球各国把眼光投向海上风电资源。筒型基础作为一种新型的海上风电基础型式,具有易于安装、节约成本和可回收利用等优点,具有广阔的应用前景[1]。筒型基础沉放过程中,土体在筒自重和负压的共同作用下受到扰动,土中孔隙水压力发生剧烈变化,土体强度受到影响,这不仅会影响筒型基础的承载能力,而且会对海底管线等周围结构物产生不利影响。因此,需要对筒型基础沉放过程的影响范围开展相应的研究[2-3]。
目前,针对吸力式筒型基础沉放过程中筒内外土体超静孔隙水压力产生和分布的研究很少[4],但筒型基础的自重沉放过程可类比于传统桩基础的贯入过程[5],因此可借鉴桩基础相应的研究方法及研究成果。朱向荣[6]通过分析沉桩过程中桩周土体孔隙水压力的实测资料,发现桩周土体超静孔隙水压力的分布随距桩中心点的距离呈对数衰减,影响范围约为30 倍桩径。姚笑青等[7]从土压力理论出发,将沉桩过程近似看作土体受水平挤压而发生破坏的过程,进而对孔隙水压力的变化进行了理论分析。
筒型基础的负压沉放过程与桩基础的正压贯入过程有很大区别,国内外学者对筒型基础的负压沉放过程进行了大量的研究。Cao[8]通过离心模型试验,研究了沉箱沉放过程超静孔隙水压力的分布规律,结果表明适用于打入式桩的圆孔扩张理论也同样可用来描述吸力式沉箱在黏土中的超静孔隙水压力分布。Chen 等[9]采用离心机试验、大变形有限元和圆孔扩张理论来研究不同筒型基础的沉放方式对于筒外部土体径向总压力的影响。Lian 等[10]进行了一系列室内试验,研究了砂土中静压和负压沉放过程中沉箱与饱和砂土相互作用的机理,并提出了计算沉放阻力与所需负压的修正公式。丁红岩等[11]通过大比尺模型试验研究了在粉质黏土中复合筒型基础沉放过程所需负压。刘润、祁越等[12-13]通过室内模型试验分别研究了在正压和负压作用下,筒型基础在无黏性土中的沉放阻力。综上所述,对于筒型基础沉放过程的研究,更多的偏重于合理确定沉阻力和所需负压,对于筒型基础沉放过程的影响范围研究很少。
本文针对我国海域粉质黏土广泛分布的特点,开展了粉质黏土中筒型基础的沉放实验,通过监测筒基内、外土中孔隙水压力和土体抗剪强度的变化,揭示了筒型基础沉放过程对周围土体的影响范围与程度。
2 室内模型试验
2.1 试验模型与材料试验模型为钢制圆筒,为了便于观察筒内情况,其顶部安装了可拆卸的法兰盘,具体尺寸见表1。

表1 试验模型尺寸
现有地勘资料显示,海洋表层黏性土不排水抗剪强度范围为5 ~10 kPa,试验中一方面参考地勘资料,同时考虑对比正负压下沉过程孔压分布需要尽量减小筒型基础初始贯入深度,最终确定制备表层土体强度为10 kPa 的黏土。试验土体取自天津港吹填区,为具有海相沉积特性的粉质黏土。填土时,首先用自制的黏土搅拌装置将土体加水搅拌为流塑状态,然后分层填入1 m×1 m×1 m 的试验槽内,静置两周后进行了真空预压固结,固结过程中使用微型十字板每隔1 h 测量一次土体不排水抗剪强度,直至土体强度达到10 kPa,此时测得的土体的物理力学性质指标如表2所示。

表2 土质参数
2.2 测试方案
(1)筒内外孔隙水压力监测:为了测量筒型基础沉放过程中孔隙水压力沿筒轴向及径向的变化,填土阶段即在土中预埋了数组孔压传感器,其中筒内两列,筒外三列,每列均为3 个,布置形式如图1所示。
(2)土体强度测试:为了研究筒基沉放对邻近土体强度的影响,试验中使用了微型十字板测量筒基沉放前后土体的不排水抗剪强度。定义,L 为测点距筒基中心的距离,r0为筒基半径,测点1 ~4 分别对应λ取值为0、0.5、1.3 和2,测点布置示意如图2所示。

图1 孔压计布置

图2 测点布置
筒型基础沉放前,测量距筒中心不同距离处土体的不排水抗剪强度Su0,取平均值作为筒基沉放前的土体强度,表3出了筒基沉放前黏土不排水抗剪强度值Su0,正压与负压沉放后土体强度以折减率形式在后文给出。

表3 筒基沉放前的不排水强度
2.3 实验步骤此次试验地点位于天津大学岩土工程实验室,分别采用静压与负压试验模拟筒型基础的沉放过程。
(1)静压沉放试验:模型筒首先依靠自身重量缓慢下沉,待筒体稳定后,连接传力架,采用伺服电机匀速加载,加载速率为0.5 mm/s,沉放总阻力通过压力传感器进行测量。静压试验装置如图3所示。试验中监测筒内外孔隙水压力的变化。Lian[10]研究结果表明,静压下沉速度对沉贯阻力基本没有影响(1 cm/s 和2 cm/s),本文试验为了分析孔压变化过程,需要尽可能减小筒型基础下沉速度,因此选择加载速度为0.5 mm/s。
(2)负压沉放实验:模型筒首先在自重作用下缓慢下沉,待筒体稳定后,连接真空泵与负压罐对筒内抽负压,直至模型筒沉放就位,筒型基础沉放深度使用位移计测量。负压试验装置如图4所示。试验中监测筒内外孔隙水压力的变化。

图3 静压沉放试验装置

图4 负压沉放试验装置
2.4 实验结果
(1)静压沉放试验结果:图5为筒型基础静压沉放试验得到的沉放总阻力和时间随沉放深度的变化曲线,图中F 为沉放总阻力,t 为时间,H 为沉放深度。
由图5可知,筒型基础的沉放阻力随沉放深度的增加线性增长。筒基在1.46 kN 的贯入力作用下共下沉19.2 cm,沉放就位后有超土塞现象,超土塞高度为0.8 cm。
筒内、外孔隙水压力的监测结果如图6所示,图中Δu 为超静孔隙水压力。
分析图6可知,随着筒型基础静压下沉,筒内外土中的超静孔隙水压力不断增加,当筒端的下沉深度达到测点深度时,测点的超静孔隙水压力达到峰值,而后下降。相同深度测点的孔隙水压力变化表明,筒内的超静孔隙水压力明显大于筒外,这是由于筒内土体受到的挤压程度大于筒外。

图5 沉放总阻力和时间随沉放深度变化曲线

图6 超静孔隙水压力变化曲线
土体中孔隙水压力的变化必然导致有效应力的改变从而影响土体的强度,定义ξ为筒型基础沉放后邻近土体的强度折减率,其中Sui为筒基沉放后土体不排水抗剪强度值。图7给出了筒基静压沉放后不同位置土体的强度的平均折减率。
分析图7发现,筒型基础静压沉放对筒内、外土体的强度产生了影响,且随着距筒基中心点距离的增加土体的强度折减率提高,当土体距筒体中心的距离等于2 r0时,土体不排水抗剪强度值Su基本不受影响。

图7 静压沉放强度折减率随间距变化规律

图8 负压和沉放位移随时间变化曲线
(2)负压沉放试验结果:图8为筒型基础负压沉放试验得到的负压和沉放深度随时间变化曲线,图中P 为负压。由图8可知,筒型基础负压沉放试验中,用真空泵持续抽负压,直至筒顶盖完全接触土体,整个试验过程历时1100 s。试验结束时发现筒内存在土塞,高度为4.8 cm。筒型基础在自重作用下沉1.2 cm,在负压作用下下沉14 cm。可以明显看出,负压沉放方式土塞高度明显大于正压沉放方式,主要有两方面原因,一方面在负压作用下筒壁排开的土体向筒内运动,导致负压沉放方式的土塞高度明显大于正压沉放方式;另一方面由于试验模型尺寸较小,试验过程中负压施加加快,导致了筒内土塞较高。

图9 超静孔隙水压力随时间变化

图10 负压沉放强度折减率随间距变化规律
筒内、外孔隙水压力的监测结果如图9所示,因PO-7、PO-8 和PO-9 在试验过程中损坏,图中未列出。
分析图9可知,筒内土中的超静孔隙水压力随着负压的施加而迅速下降,且越靠近土面,超静孔隙水压力下降幅度越大,说明越靠近负压源的土体中超静孔隙水压力受到的影响越大。在负压沉放结束时,筒内中心处距土面3 cm 处孔压计PI-4 的测量值为-6 kPa,PI-1 的测量值为-5.5 kPa,即筒基中心点处的超静孔隙水压力绝对值最大。筒外土中超静孔隙水压力随着筒型基础的下沉略有提高,说明负压源对筒外超静孔隙水压力影响较小。
图10给出了筒基负压沉放后不同位置土体的强度折减率。分析图11可知,筒型基础负压沉放对筒内、外土体的强度产生了影响,随着距筒基中心点位置的增长而土体的强度折减率提高。当土体距筒基中心的距离大于2 r0时,土体不排水抗剪强度值Su基本不受影响。

图11 筒壁沉贯挤土效应
3 筒型基础沉放影响范围研究
3.1 基本假定将环形筒壁看作紧密排列的等直径圆柱体,筒壁沉放过程类似沉桩挤土过程,忽略圆柱体之间的相互作用,可将筒壁挤土过程看作圆孔扩张问题,如图11所示。
图11中a0为圆柱孔的初始半径;au为扩张后的终孔半径;ap为塑性区半径;up为塑性区外侧边界的径向位移; pu为最终压力;σr为径向挤土应力;σθ为切向挤土应力;r 为计算点距筒壁中心点的距离; μ 为土的泊松比;E 为土体的弹性模量;c 为土的黏聚力;φ 为土的摩擦角。
3.2 静压沉放影响范围理论推导考虑单元力系的平衡,可以得到平面应变轴对称问题的平衡微分方程为[14-15]:

由应力平衡条件与边界条件可知,在弹性区和塑性区的交界处,有:


式中:q 为初始应力,q=γ′HK0,其中γ′为土的有效容重;H 为距土面距离;K0为静止土压力系数。
为了确定最终压力pu,可假定筒壁排开的土体体积等于弹性区体积变化与塑性区体积变化之和,则有:

式中:au=0.5δ,δ为筒壁厚度;Δ为塑性区平均体积应变,取值范围为0~0.0054[16];L1为筒裙高度。
展开式(5),略去up的高阶项和项得:


超静孔隙水压力以平均法向正应力增量Δσo和八面体剪应力增量Δτo计算,根据Henkel公式[17],有:

式中:αf及β 为Henkel 孔隙水压力系数(土完全饱和时β=1)。
圆形孔为平面应变问题,考虑到土体不可压缩,可得:

式中: Ir为刚度指标,
平均法向正应力增量Δσo为:

八面体剪应力增量Δτo为:

可以认为当Δu=0,得到静压沉放最大径向影响范围Rmax的表达式为:

其中:
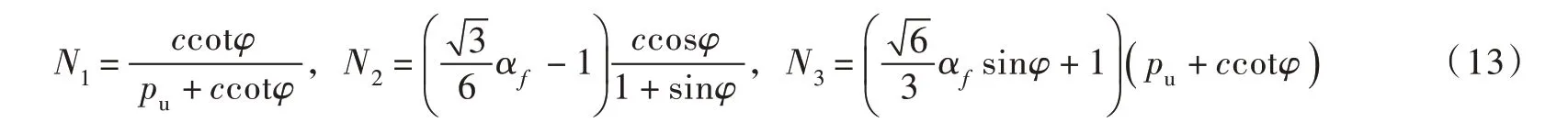
3.3 负压沉放影响范围理论推导假定筒外土中水向筒渗流的方向以水平向为主,近似按平面应变轴对称问题研究,渗流方向指向孔内,如图12所示,R1为距圆孔中心距离; p1为外水压力。
考虑渗流体积力的平衡微分方程为[18]:

式中pw为渗流体积力[19]:

图12 渗流体积力

与静压沉放推导过程相同,可计算出孔内的最终压力:

其中:

超静孔隙水压力根据Henkel 公式[17]计算,同样假定Δu=0时对应的距离为负压沉放的最大径向影响范围Rmax:

由于负压沉放过程中,筒壁排开土体部分进入筒内形成超土塞,筒壁对外侧土体挤压减弱,在计算中考虑对au的折减,即au=η( 0.5δ),建议η 的取值范围为0.6~0.8。

3.4 影响范围由模型试验结果可知,筒型基础静压和负压沉放对筒外土体造成影响,为了进一步分析影响规律,将筒外土面以下3 cm、10 cm 和17 cm 的孔压计分别记为U-1、U-2、U-3,将超静孔隙水压力和距离进行归一化处理[20],其中σ′vo为上覆有效应力,并将归一化后的实测数据绘制于半对数坐标系内,如图13所示,图中实线部分为试验数据的拟合曲线。
图13中试验数据拟合曲线与横轴的相交点,为筒基静压沉放产生的超静孔隙水压力零点,得土面以下3 cm、10 cm、17 cm 的影响范围分别为20.4 cm、21.6 cm、22 cm。图14为试验数值和理论结果的比较图,理论计算参数取值为:c=5 kPa,φ=13.2°,E=3.5 MPa,μ=0.5,γ′=9 kN/m,Δ=0.001,δ=0.006 m,αf=1.74,r0=0.1 m。

图13 静压沉放的筒外侧超静孔隙水压力分布
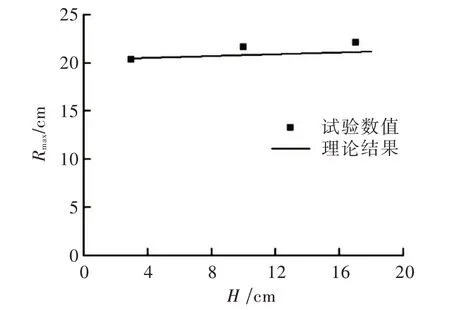
图14 试验数值和理论结果的比较

图15 负压沉放筒外侧超静孔隙水压力分布

图16 试验数值和理论结果的比较
从图14可知,理论结果与实测数据吻合较好,验证了式(12)的可靠性,Rmax与H 呈规则的线性关系。可得到筒基静压沉放对周围土体影响的最远距离约为2.2 r0,该距离随土层深度的增加而略有增加。
图15为负压沉放筒外侧超静孔隙水压力分布图,图中实线部分为试验数据的拟合曲线。图中试验数据拟合曲线与横轴的相交点,为筒基负压沉放产生的超静孔隙水压力零点,得土面以下3 cm、10 cm、17 cm 的影响范围分别为16.2 cm、16.4 cm、16.1 cm。图16为试验数值和理论结果的比较图,理论计算参数取值为:c=5 kPa,φ=13.2°,E=3.5 MPa,μ=0.5,γ′=9 kN/m,Δ=0.005,δ=0.006 m,αf=1.74,r0=0.1 m,R1=0.2 m,p1=10 kPa。
从图16可知,理论结果与实测数据吻合较好,验证了式(18)的可靠性,Rmax与H 呈规则的线性关系。可得到筒基负压沉放对周围土体影响的最远距离约为1.6r0,该距离随土层深度的增加而略有减小。
4 结论
筒型基础安装过程会扰动周围土体影响其承载能力,同时也会对周围海底管线等邻近结构物产生不利影响,因此研究筒型基础安装过程影响范围和程度具有重要意义。本文通过室内小比尺模型试验,以土体不排水抗剪强度和孔隙水压力参数的变化为依据,研究并分析了粉质黏土中筒型基础静压与负压沉放的影响范围,同时通过理论推导给出了最大影响范围的计算方法。具体结论如下:
(1)试验发现,筒型基础静压沉放过程中,当筒端下沉深度达到测点深度时,测点的超静孔隙水压力达到峰值,而后下降;筒型基础负压沉放过程中,筒内土中的超静孔隙水压力随着负压的施加而迅速下降,且越靠近土面,超静孔隙水压力下降幅度越大,筒外超静孔隙水压力随着筒型基础的下沉略有提高。
(2)理论推导最大影响范围计算方法与实验结果吻合较好,即筒型基础静压沉放对周围土体影响的最远距离约为2.2 r0,该距离随土层深度的增加而略有增加;负压沉放对周围土体影响的最远距离约为1.6 r0,该距离随土层深度的增加而略有减小。
(3)试验发现,筒型基础静压和负压沉放方法均对筒内、外土体的强度产生了影响,且随着距筒基中心点位置的增长而土体的强度折减率提高,当土体距筒体中心的距离等于2 r0时,土体不排水抗剪强度值Su基本不受影响。

