基于P-PID控制器对共轴双旋翼飞行器的姿态控制
吴东旭,丁 茹,张梓嵩,徐九龙
(沈阳理工大学 机械工程学院,沈阳 110159)
近年来,无人机发展非常迅速,无人机进入小型化、微型化时代,传统的固定翼或单旋翼直升机结构可能不再是一种最优化设计[1]。共轴双旋翼飞行器由于其外形尺寸小、推重比大、气动对称等特点,有很大的发展前景。但共轴双旋翼飞行器模型复杂度高、耦合性强,在飞行过程中是不稳定系统,造成大多数飞行控制算法难以保证飞行的稳定性[2]。虽然现代控制理论发展日益完善,有许多先进的控制算法和理论,但在工程中基于经典PID的控制算法仍然是最普遍、最有效的控制方案[3]。对于共轴双旋翼飞行器的姿态控制,传统的PID控制算法效果不理想[4],系统鲁棒性较差,为了提高系统的稳定性,本文采用P-PID控制器对共轴双旋翼姿态进行控制,提高系统的鲁棒性。
1 PID控制原理
PID控制系统原理框图如图1所示。

图1 PID控制系统原理框图
PID控制器是一种线性控制器,它根据给定的期望值r(t)与实际输出的反馈信号c(t)之差构成控制偏差e(t)[5],e(t)=r(t)-c(t)将控制偏差分别与比例项、积分项和微分项通过线性组合的形式构成控制量,对被控对象进行控。其结构形式为:
(1)
式中:u(t)为系统输出;KP比例系数;KI积分系数;KD微分系数。对于数字系统可将其离散化,得到离散化的PID公式[6]
(2)
由于共轴双旋翼飞行器在悬停状态下是不稳定且非线性系统,在飞行过程中,遇到磁场干扰、风阻会使传感器数据采集失真,解算出的姿态角有误差,只用单级角度PID控制系统很难使飞行器稳定运行,飞行效果不好,为了解决这一问题,本文提出采用P-PID控制器。
2 串级P-PID控制器
P-PID控制器是由两个控制器串联在一起工作,其系统框图如图2所示。GC1(s)为主调节器传递函数,包含GC1(s)的外环为主回路,G1(s)为系统的主控对象,G2(s)为副控对象,R1(s)为系统输入量,Y1(s)为系统的输出量。GC2(s)为副调节器的传递函数,包含GC2(s)的内环为副回路Y2(s)为副调节器的输出量。主调节器的输出量U1(s)为副回路的输入量R2(s),D2(s)为外部干扰信号[7]。因为内环控制器与执行机构近,所以副回路是串级系统设计的关键。
由副回路系统框图可得副回路闭环的传递函数为
(3)
式中可得副调节器控制规律
(4)

图2 串级控制系统框图
飞行器通过串级P-PID对姿态进行控制,机体的陀螺仪得出三轴角度、角速度,GPS给出机体空间位置信息,加速度计得到三轴的加速度值。外环作用于角度差产生内环期望角速度[8],内环作用于角速度差产生期望的推力,经过混控器发出PWM信号作用于电机和舵机,通过负反馈信息最终对飞行器进行姿态控制。
3 飞行器仿真分析
通过Creo2.0建立共轴双旋翼飞行器模型导入到Matlabsimulink中进行仿真,其仿真系统图如图3,分析对比试验效果。飞行器相关环境参数设置:机体质量m=2.17kg,空气密度rho=1.2kg/m3,上桨的转动惯量Jup=0.28kg·m2,下桨的转动惯量hdown=0.12kg·m2,初始姿态横滚角roll=0°、俯仰角pitch=0°,PID控制器相关参数为Kp=20、Ki=1、Kd=1。其仿真结果如图4所示。

图3 仿真系统

图4 PID、P-PID控制器仿真结果
4 飞行器姿态控制试验
图5为验证控制算法的共轴双旋翼飞行器。

图5 共轴双旋翼飞行器样机
PID控制器从0°到期望1°的收敛时间约为7s,P-PID控制器的收敛时间约为1.5s,系统的超调量减少约10%。仿真结果表明:P-PID控制器的收敛效果明显好于PID控制器,缩短了系统收敛时间,减小了系统的超调量,提高了系统的稳定性和可控性。图6为P-PID算法流程图。

图6 P-PID算法流程图
将图6算法烧录到嵌入式系统中,进行大量的现场飞行试验和参数整定,最终飞行器能实现很好的飞行效果。实际飞行试验的P-PID参数ROLL_P=6.5、ROLLRATE_P=0.11、ROLLRATE_D=0.005、PITCH_P=6.5、PITCHRATE_P=0.11、PITCHRATE_I=0.05、PITCHRATE_D=0.005,通过调用飞行日志,将飞行中的姿态数据导入到Matlab中描绘出飞行器在飞行过程中的横滚角(roll)、俯仰角(pitch)、横滚角速度(rollspeed)、俯仰角速度(pitchspeech)。图7为实际飞行中姿态角度和角速度。
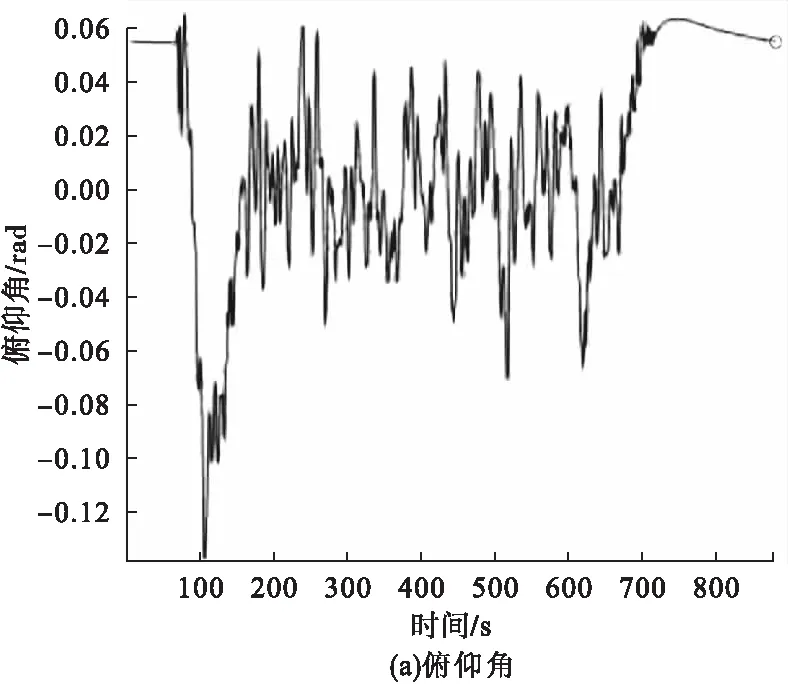

图7 飞行姿态数据
对数据进行比对分析可知飞行器在空中的横滚角和俯仰角的误差在0.05rad以内。整体飞行过程比较平稳,角速度波动大约为1rad/s,说明系统的响应速度较快,在短时间内能平稳收敛,系统的超调量也较小,通过对飞行试验数据分析验证了算法的可行性且有良好的控制效果,为以后的飞行试验奠定基础。
5 结束语
本文对传统的PID进行改进,采用P-PID控制器对姿态进行控制,通过试验大约3s飞行器达到稳态,姿态角度误差约0.05rad,获得了良好的姿态控制效果,验证了该算法在实际工程中的可行性。

