浅海复合探测方法研究

李 环，迟秀秀

(沈阳理工大学 信息科学与工程学院，沈阳 110159)

目前，深海有效声速法已经成功应用于深海域，但还无法处理由浅海环境下声速传播的多途效应所引起的干扰，且浑浊的水质容易吸收声信号，使得远距离信息的传播和探测更加困难[1]。在浅海目标探测的研究中，目标源所产生的振动，一定存在一部分振动能量以振动波的形式、以震源为中心在海底向四周传播，这部分以声波形式传播的信号可直接由被动声呐传感器采集；同时这部分振动能量会引起海底的振动，使海底成为二级震源，继续向四周传播，这种在海底以地震波形式传播的信号称为海底地震波，可利用振动传感器进行采集，海底地震波的存在为实现复合探测提供了可能。

近年来，国内外不少学者从不同的角度对浅海目标探测方法进行了研究，但仍无法完全消除多途效应的干扰，探测精度不理想[2-3]。因此，本文借助多途效应的现象，利用同一震源的两种不同传播途径进行复合，即在Daubechies系列小波滤波处理基础上，利用滤波后目标振动信号声波和地震波形式实现复合探测，获取目标振动信号在两种不同传播途径的时延值，进而较准确实现对目标的探测。

1 多分辨率分析及小波分解

通过尺度的变化，用不同尺度的小波来观测时域信号的方法称为多分辨率分析[4]。原始声波及地震波形式的信号中既包含目标振动信号也含有非目标振动信号；随着科学技术的发展，浅海中目标振动所产生的信号频率越来越低，一般的滤波方法对低频或甚低频的信号提取效果不佳，因此，利用多分辨率分析对原始声波及地震波信号做滤波处理，以较准确获取低频或甚低频目标振动信号。

通常选用Daubechies系列小波对此类信号进行处理，在选用的小波具有正交性、紧支撑、对称性、光滑性、正则性和消失矩的情况下，L2(R)中的嵌套闭子空间序列{Vj}j∈Z称为L2(R)的一个多分辨率逼近。

Vj+1⊂Vj,Vj∈Z

(1)

f(t)∈Vj+1⟺f(2t)∈Vj,∀f(t)∈L2(R),∀j∈Z

(2)

(3)

(4)

存在θ，使得{θ(t-n)}n∈Z是V0的Riesz基。将Riesz基{θ(t-n)}n∈Z通过正交变换可以得到一组正交基{φ(t-n)}n∈Z，其中φ(t)称为尺度函数。

按照投影定理，Vj可分解为Vj+1及其正交补集Wj+1的直和，即

Vj=Vj+1⊕Wj+1,Vj+1⊥Wj+1,j∈Z

(5)

令Dj等于L2(R)到Wj的正交投影算子，则

fDj(t)=Djf(t)

(6)

表示f(t)在Wj上的正交投影，也可叫做f(t)在分辨率为2-j下的细节信息。由式(5)可得

fAj(t)=fAj+1(t)+fDj+1(t)

(7)

fAj(t)比fAj+1(t)包含了更多的信息，其余无用的信息则会包含在fDj+1(t)中，fAj+1(t)包含了fAj(t)的低频部分，fDj+1(t)包含了fAj(t)的高频部分，Vj称为尺度函数空间，Wj称为小波函数空间。

对于任一正整数M而言，fN有唯一的分解

fN(x)=gN-1(x)+gN-3(x)+…+gN-M(x)+

fN-M(x)

(8)

式(8)中

且还可写成

(9)

因此，式(9)中序列{cj+1,n}与{dj+1,n}可唯一确定式(8)的分解形式。

从文献[4]可知，φ(x)与φ(x)的二尺度关系为

(10)

式(10)中，pn和qn分别为差分方程中离散细节权重和平滑逼近权重，φ(x)与φ(x)分别为小波函数和尺度函数，且φ(x)与φ(x)的分解关系为

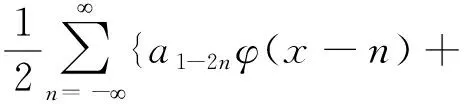
b1-2nφ(x-n)},l∈Z

(11)

式(11)中

应用分解关系式,将式(11)代入式(9)可得到

+b1-2nφ(2jx-n)}]

(12)

根据分解式fj+1(x)=fj(x)+gj(x)，即式(12)和式(9)表达式之间存在恒等关系，推导可得

由{φl,n:n∈Z}与{φj,n:n∈Z}的l2线性无关性以及Vj∩Wj={0}，可得分解算法如下。

(13)

因此，以多分辨率理论及小波分解算法为依据，可将原始声波及地震波信号进行多层分解，较准确逼近所需的目标振动信号，为进一步利用处理后的目标振动信号的声波及地震波形式进行复合提供条件。

2 复合探测的实现

在多分辨率分析的基础上，将滤波处理后的目标振动信号的声波及地震波形式进行相关运算以实现复合探测，且可获得同一种信号在两种不同传播途径的时间延迟。所谓时间延迟，是指传感器阵列中不同传感器接收到的同源信号之间由于传输距离不同而引起的时间差，即互相关函数的峰值所对应的时延即为真实时延的一个估值[5]。因此，利用Daubechies系列小波所提取的目标振动信号声波和地震波形式进行相关，获取目标产生的信号在两种不同传播途径的时延估计值，并与时延真值进行对比，以对复合探测方法进行初步验证。

假设传感器A、B接收到的信号为x1(t)、x2(t)，s(t)为目标声源信号，D为时间延时，n1(t)、n2(t)为加性噪声。假定n1(t)、n2(t)、s(t)互不相关，两传感器接收信号的模型为

x1(t)=s(t)+n1(t)

x2(t)=s(t-D)+n2(t)

(14)

式中D既为所要估计的信号到达两个传感器的相对延迟时间。

确定两个相关信号之间时延的最直接方法就是互相关函数法

R12(τ)=E[x1(t)x2(t+τ)]

=Rss(τ-D)+Rsn1(τ-D)+Rsn2(τ)+

Rn1n2(τ)

由上述假设n1(t)、n2(t)、s(t)互不相关，可得

R12=Rss(τ-D)

(15)

式中Rss(τ)为源信号s(t)的自相关函数。由自相关函数的性质可知Rss(τ-D)≤Rss(0)，即当τ-D=0时，两接收信号相关性最大，选择相关函数峰值点位置作为时延估计值。

传感器A与传感器B所接收信号同为一种形式，即传播速度相同。相同形式信号的实际目标与传感器位置示意图如图1所示。

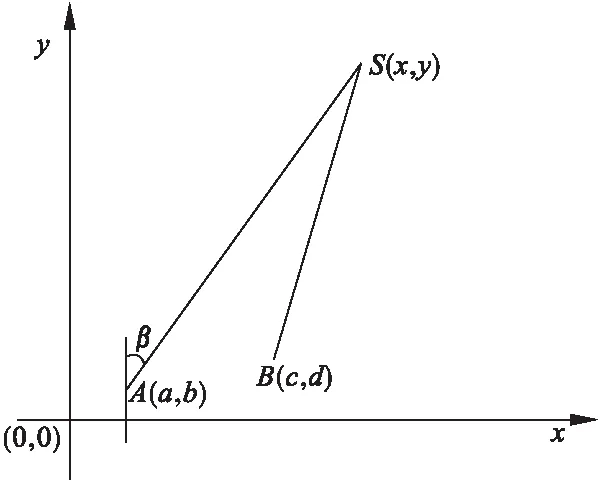
图1 相同形式信号目标与传感器位置示意图

如图1直角坐标系中，声源坐标设为S(x,y)，传感器A(a,b)，传感器B(c,d)，相同形式信号的速度设为C，则目标声源信号到达两个传感器的时延真值为

Δt=

(16)

传感器A与传感器B所接收信号为同一信号的不同种形式，即传播途径不同，传播速度不同。以来自同一目标振动信号，不同传播途径所接收的海底地震波与声波形式为例，不同形式信号的实际目标与传感器位置示意图如图2所示。

如图2中的直角坐标系所示，将声源坐标设为S(x,y)，传感器A、B均放置于坐标原点(0,0)处，传感器A、B因产品尺寸大小产生的距离忽略不计。设目标振动信号的声波形式传播速度为C1，海底地震波形式的传播速度为C2，忽略辐射传播到海底的时间，则目标声源信号到达两个传感器的时延真值为

图2 不同形式信号目标与传感器位置示意图

(17)

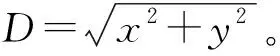
以上述复合探测实现原理为依据，利用两个振动传感器和被动声呐传感器，根据图1和图2所示的目标与传感器示意图进行相应置位，对复合探测方法进行实验验证。

3 探测实验对比分析

3.1 实验数据的采集

本实验需与只利用地震波形式信号所得结果进行对比分析，实验设备连接示意图如图3所示。

图3 实验设备连接示意图

利用500斤重4cm厚的钢板模拟目标，当120斤重的铁锤敲击钢板使震源产生信号时，通过连接水下振动传感器和声呐传感器的采集系统对数据进行采集。

当幅值的测量范围在-5～5v之间，采样频率为2048Hz时，所采集到的地震波及声波数据波形图及频谱图如图4所示。

图4 地震波和声波实验波形及频谱原始数据图

由于面波的频率范围为10～80Hz，观察图4a和图4c可知，地震波实验数据包含有效目标波信号的频率范围为50Hz以内；观察图4b可知，声呐所采集的声波干扰较少，主要频率集中在0.5053Hz处，且图4c传感器B的频谱图中也包含此频率，由此可知本次实验数据较符合理论基础。

3.2 地震波探测

从图4a中观察可得，传感器A的地震波实验数据的频谱图中，频率大部分集中在50.03Hz处，

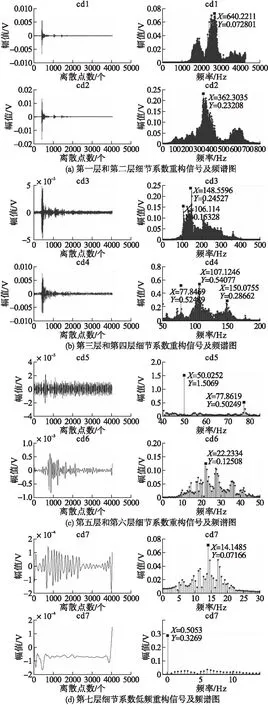
图5 传感器A地震波七层系数重构信号及频谱图

由于面波的频率范围为10～80Hz，所以频谱中其他两个高于80Hz频率不作为考虑，实验所设采样频率为2048Hz，且为获得全面有效的信号，同样利用Daubechies系列小波对传感器A采集的地震波实验数据进行七层小波分解，七层滤波细节系数重构信号及频谱图如图5所示。

由图5可知，传感器A滤波后的地震波实验数据时域图可清晰看到目标波信号波形。从图5d可知，地震波实验数据第七层细节系数重构信号的滤波结果主要频率集中在14.1485Hz处；地震波实验数据第七层低频重构信号的滤波结果主要频率集中在0.5053Hz处，因此，选择传感器A的第七层低频重构信号作为提取信号。

同样观察图4c可知，传感器B的地震波实验数据频率大部分集中在50.03Hz处，由于面波的频率范围为10～80Hz，所以频谱中高于80Hz频率不作考虑。实验所设采样频率为2048Hz，为获得全面有效的信号，利用Daubechies系列小波对传感器B采集的地震波实验数据进行七层小波分解；传感器B同样选择第七层低频系数重构信号作为提取信号，其第七层低频系数重构信号如图6所示。

图6 传感器B第七层低频系数重构信号图

由图6可清晰看到目标波信号波形。为验证只利用地震波进行相关的效果误差大小，将图5d中振动传感器A第七层低频系数重构信号与图6中振动传感器B第七层低频系数重构信号进行相关运算，结果如图7所示。

由图7可知，相关运算最大值在-1.3091s处，即在此处所提取的两地震波信号存在最大相似性，相关系数大小为0.48192，即时延为1.3091s。

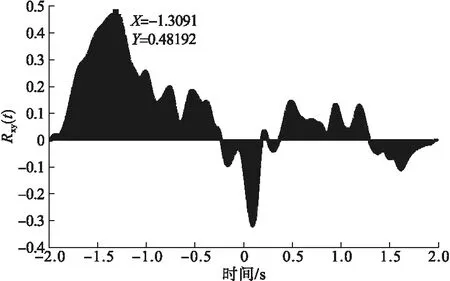
图7 两地震波形式目标振动信号相关图

3.3 复合探测

从图4b中观察可得，声波实验数据的频谱图中，频率大部分集中在10Hz以内，而实验所设采样频率为2048Hz，所以仍利用Daubechies系列小波对声波实验数据进行七层小波分解，七层小波变换细节系数重构及频谱图如图8所示。

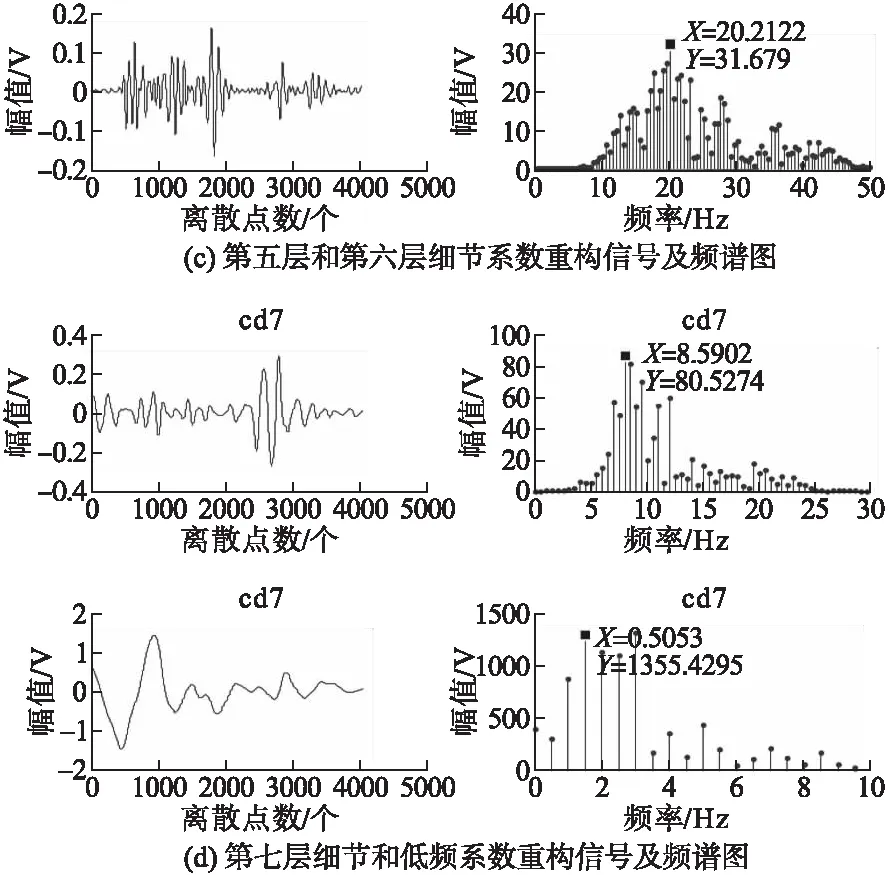
图8 声波七层细节系数重构信号及频谱图

从图8可清晰看到目标波信号波形；图8d声波实验数据第七层细节系数重构信号的滤波结果主要频率集中在8.5902Hz处，声波实验数据第七层低频重构信号的滤波结果主要频率集中在0.5053Hz处，因此选择声波实验数据第七层低频重构信号作为提取信号。

利用声波实验数据和地震波实验数据所提取的第七层低频系数重构信号作为探测信号，进行相关分析，以获得目标振动信号在两种不同路径的传播时间，相关运算结果如图9所示。

图9 地震波和声波第七层低频信号互相关图

由图9可知，目标振动信号经过两种不同传播途径所得时延为+0.71582s，即在0.71582s处两信号波形最相似，相关性最高，相关系数为0.27452。

3.4 地震波探测与复合探测对比分析

为对复合算法进行验证，将两个振动传感器与声呐传感器置于同一水平面上，即与震源的垂直距离相同。实验所设目标振源S(0,0)，两振动传感器的坐标分别为A(190,-90),B(-30,-90)，且声呐传感器与传感器A放置于同一位置，将其位置值代入式(15)、式(16)可得实际时延。查表可得声波在海水中速度为1500m/s，实验场地通过鉴定介质为泥沙，泥沙中横波传播速度为200m/s，因此，本实验中海底地震波的速度为184m/s[6-7]。分别利用两振动传感器A和B、振动传感器A和声呐传感器进行滤波处理，将所得时延与实际时延真值进行误差对比，对比结果如表1和表2所示。

表1 地震波探测技术实验结果

表2 复合探测技术实验结果

对比表1和表2可得，利用目标振动信号的地震波形式所得的时延相比实验时两振动传感器时延真值所得误差值为0.4395s；利用声波和地震波两种形式所得时延相比实验时的时延真值所得误差为0.1766s，这与理论分析的时延误差趋势一致，可知利用声波和地震波形式相复合比只使用地震波形式信号所得时延更接近实际结果。观察表1和表2中的相关系数，在相同环境和相同震源情况下，利用声波和地震波进行复合所得相关系数小于只利用地震波形式信号进行相关所得相关系数，源于振动传感器所接收的信号相比于声呐所接收信号在传递过程中存在很大衰减，而声波形式的信号在浅海中衰减较小，经过滤波处理后，所得信号中包含的目标振动信号的强度相比于地震波形式的信号大，且比地震波形式的信号包含的目标振动信号的有效信息全面，因此，声波与地震波信号相似程度低于两个地震波形式的信号相似程度。

4 结 论

(1)由于地震波的衰减特性，单一利用地震波进行探测，无法对地震波衰减引起的误差进一步消除。

(2)利用目标振动信号的地震波形式所得的时延与实验时两振动传感器时延真值的误差值为0.4395s，利用声波和地震波两种形式所得时延与实验时的时延真值的误差为0.1766s，可知利用同一信号的声波和地震波两种形式进行复合探测，可将探测精度的可靠性提高20%。