基于遗传算法的双目标混合流水车间调度问题研究
李文韬,陶 泽,陈晓菲
(沈阳理工大学 机械工程学院,沈阳 110159)
科技高度发展的今天,单一的目标已经不能满足企业生产的需要。在实际生产问题中有很多是属于双目标的优化问题,其理论与方法也一直是研究讨论重点,因此研究双目标问题有重要意义[1]。混合流水车间调度问题(HFSP)作为一般流水车间调度问题的推广,是一种更加复杂的问题,其主要特征为加工过程中某些工序存在并行机器调度,因此需要解决工件在各并行机器的分配。
对调度问题,相关学者已提出运筹学方法、启发式方法、神经网络方法等对问题进行求解。但这些方法具有周期长、解质量差等缺点,不太适用于工程问题。相比而言,小生境遗传算法可兼顾遗传算法良好的全局搜索能力及小生境技术维持种群多样性的优点[2]。相关学者已经成功的利用遗传算法解决调度问题。Davis[3]把遗传算法的思想运用到车间调度问题中,成功的取得了车间调度问题的最优近似解;张思源等[4]设计混合遗传算法,解决置换车间和非置换车间两种情况下的流水车间调度问题。本文以生产周期和生产费用为目标,运用小生境遗传算法,利用软件进行仿真优化,得出调度甘特图,并给出最优方案。
1 双目标混合流水车间调度问题的描述
对于流水车间,企业往往需要在双目标约束下进行加工生产,若调度能同时满足目标条件,则生产就能达到较高水平。本文研究以生产周期-生产费用为双目标的流水车间调度问题,所建立的数学模型如下。
最小化生产周期
(1)
最小化生产费用
(2)
式中:f1为生产周期;f2为生产费用;Lik为工件i在机器k上的加工时间;Ci为工件i的生产成本;n为工件总数;i为加工零件;k为加工机器。
HFSP是由一般流水车间调度问题推广出来的,在现实生产过程中普遍存在。HFSP描述如下:n个工件在m台机器上进行流水作业加工(m>n),每个阶段至少存在一台机器,且至少有一个阶段存在并行机器,要求相同工序的并行机器加工性能相同;已知各工件的加工时间,最终求得工件的加工顺序及并行机器的分配情况[5]。建立的数学模型如下。
(3)
(4)
(5)
Mj≥1
(6)
(7)
Cij≤Bir,r=j+1
(8)
式中:n为待加工的工件数;Xip为0~1变量(若工件i被安排在第p个位置上则取值为1,否则取值为0);Mj为工序j的并行机器数量;Yijk为0~1变量(若工件i的第j道工序被安排在第k台机器上则取值为1,否则取值为0);m为工件所需的工序数;Cij为工件i在工序j上的加工完成时间;Bir为工件i在工序r上的开始加工时间。式(3)和式(4)表示每个位置被分配一个工件,且每个工件只能有一个优先级顺序;式(5)表示每阶段的任务只能由一台机器加工;式(6)和式(7)表示所有工序中至少存在一个工序有并行机器;式(8)表示只有当前工序完成后才能进入下一道工序。
2 遗传算法和小生境技术结合的调度算法
遗传算法基本原理是把所求解的问题采用编码的方式编成染色体,每个染色体代表被求问题的一个解。然后对种群中的每个个体进行评价,若不满足算法的终止条件,则算法通过适应度值的大小进行降幂排列来评价个体的优劣程度,挑选优秀的个体构成下一代种群,进行选择、交叉、变异操作,一代代不断地进行遗传,直至结果达到算法收敛条件,获得最优的个体。由于遗传算法一般是优先选择更高级别染色体进行复制,往往收敛于局部最优解,降低了遗传算法的全局搜索能力,无法保证解的多样性,为此引进小生境技术解决多目标调度问题,可获得全局最优解[6]。小生境技术的基本思想是将每一代个体划分为若干类,在每类中选出适应度值大的个体作为优秀个体代表组成一个种群,再在种群内部及不同种类之间通过遗传操作产生子代种群,采用预选择机制完成选择操作。对于同级别的染色体,通过小生境技术可选出更好的个体进行复制。改进后的遗传算法流程图如图1所示。
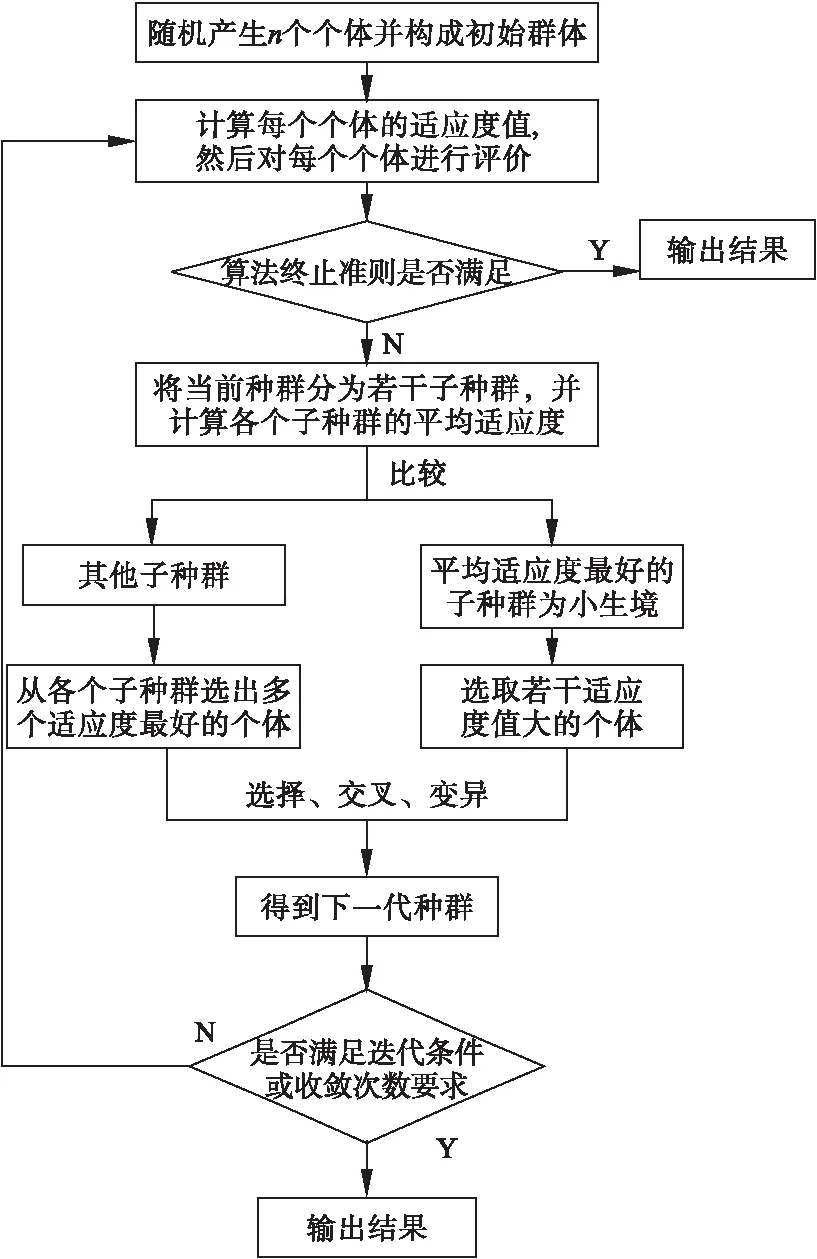
图1 算法流程图
3 双目标混合流水车间调度的算法实现
3.1 编码与解码
本文对HFSP采用的是矩阵编码,这种方法的优点是能很好的解决工序之间的约束关系,使得染色体与可行调度能一一对应,在遗传操作中也不会产生非法解。
(9)
矩阵中的元素ast都是区间(1,Ms+1)里的一个实数。对矩阵中的元素进行取整,当出现取值相同时,说明至少两个工件在同一机器上进行同一工序的加工。此时分两种情况进行考虑:(1)所取的工序为第一道时,加工顺序可以按照a1t的升序进行加工;(2)所取工序为第二道或之后的工序,根据前一道工序的完成时间再确定其加工顺序,前一道工序先完成的先加工,若加工完成时间相同,按照ast的升序进行排序加工。
矩阵编码完成后,可以确定染色体。每条染色体皆由s段构成,每段由t个基因构成。段与段之间用标识符断开,标识符用“0”表示,代表不同工序,因此染色体的长度为s(t+1)-1。染色体表示形式为
[a11,a12,…,a1t,0,a21,a22,…,a2t,0,…,as1,as2,…,ast]
3.2 产生初始种群
运用小生境遗传算法进行运算时,初始种群的产生特别重要。若产生的初始种群适应度值较低,则不利于初始小生境环境的产生,影响全局的搜索效率;相反,若产生的初始种群适应度值较高,则算法会快速的进行搜索,找到局部的最优解[7]。本文中,初始种群的产生方式为随机产生,其染色体的表现形式与编码的方式相同。
3.3 适应度函数
遗传算法在进行计算时只运用适应度函数进行个体优劣的评价[8]。对于双目标问题,所求目标为全局的最小值,故可将目标函数进行一系列的转换,最终确定适应度函数为
(10)
式中Cmax(X)为算法计算过程中的最大值。
3.4 选择操作
选择操作是在现有群体中选择出优良的个体进行下一代的遗传[9]。当选取优先级别不相同的染色体时,采用比例选择法进行选取。当优先级别相同时,利用小生境技术进行选取[10],选择的基本思想是通过计算小生境数选出更加优秀的个体进行遗传,计算原理如下。
计算小生境的半径
(11)
进行统一纲量
(12)
计算每个个体之间的距离
(13)
计算小生境数
(14)
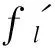
3.5 交叉操作
编码方式为矩阵编码,因此只需要满足ast∈(1,Ms+1)这个条件,即可确保个体的合法性[11]。在本文中,采用两个矩阵按行进行交叉操作。举例进行具体说明。
设父代P1和P2的染色体编码如下。
若按行进行交叉操作,交叉点随机选择为2,则产生两个新的染色体
3.6 变异操作
变异操作是将原染色体基因转变成新染色体的过程[12]。本文采用的变异操作为逆转方式,即随机选取染色体中的一部分基因作为子串,然后将该子串进行逆转,以相反的顺序排列后再重新放回原先的子串位置。
4 算例仿真
本次算例仿真是以生产周期和生产费用为研究目标,对双目标混合流水车间调度问题进行最优化处理。采用Delphi7.0软件,运用面向对象的技术进行编程,运行上述算法。在进行优化过程中,作出以下假设:工件的加工时间和加工顺序确定,每个工件的各项加工参数不变。在假设的基础上进行加工,使工件依次进入流水车间进行生产,最终完成加工目标。在本次仿真中,采用的工件数为8个,每个工件有6道工序,其中并行机器的设置为:第二道工序的并行机器为2台,分别为机器M2、M3;第三道工序的并行机器为2台,分别为机器M4、M5;第五道工序的并行机器为2台,分别为机器M7、M8。把工件的非并行机器加工时间和并行机器的加工时间分别列在表1、表2中,表1为工件在非并行机器上的加工时间,表2为工件在并行机器上的加工时间。
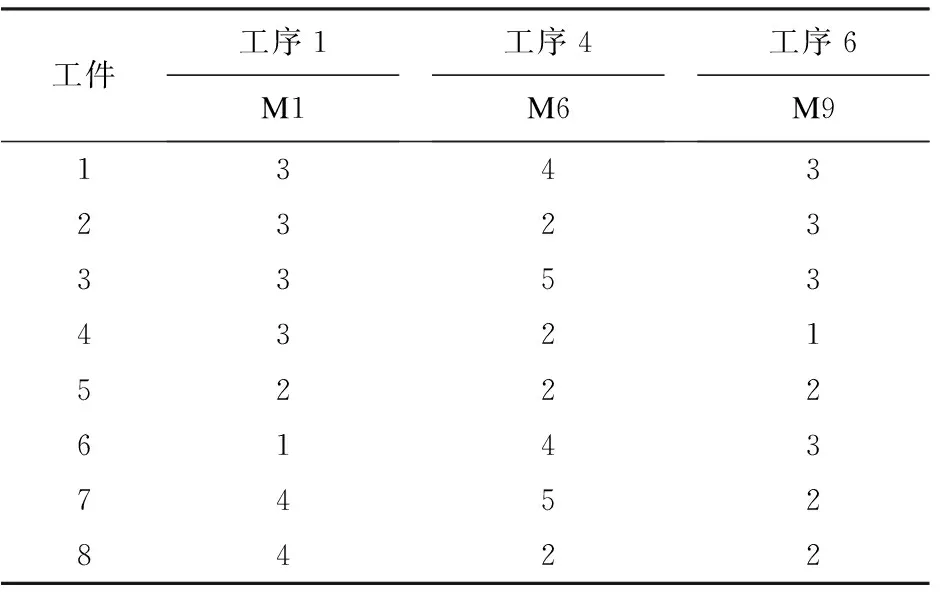
表1 各工件在非并行机器上的加工时间 分钟
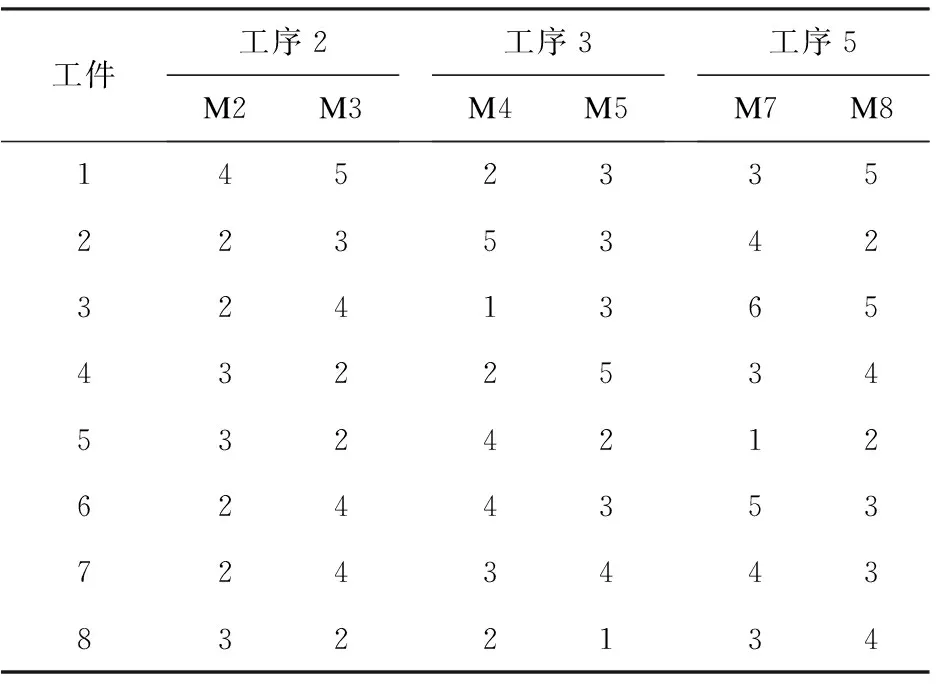
表2 各工件在并行机器上的加工时间 分钟
运用小生境遗传算法解决问题,所设定的参数为:各个机器的初始加工时间均设为0,种群数目为100,交叉所占比率为0.8,变异所占比率为0.1,迭代次数为200。利用软件计算最优结果,进行8次仿真运算,仿真次数与对应的生产周期见表3。

表3 仿真次数与生产周期
表3中计算的是混合流水车间中生产周期的最小值,通过表中的数据可以看出,生产周期皆在36~38分钟,数据虽有起伏但变化不大,相对平稳,符合算法的有效性和可行性。软件通过小生境遗传算法进行计算,得出生产周期和生产费用的最优结果。各台机器的生产费用见表4。

表4 机器生产费用
在双目标优化过程中,通常所求的是目标的最大值或最小值,本文所求的是生产周期最短和生产费用最小。确定双目标的最优解时,利用双目标空间定级图可快速进行研究、分析。在双目标最小化问题中,如果其空间中存在一个个体的横坐标和纵坐标都比空间中其它个体小,那么可设定该因子为支配因子(在种群中,能支配其它任意个体的因子),将其定为级别0;依次类推,如果在空间中一个个体只存在一个横坐标或纵坐标大于之前的横坐标或纵坐标,则其定为级别1,直至空间中所有的个体级别全部被定级完毕。
图2是运用小生境遗传算法得到的后代示意图。
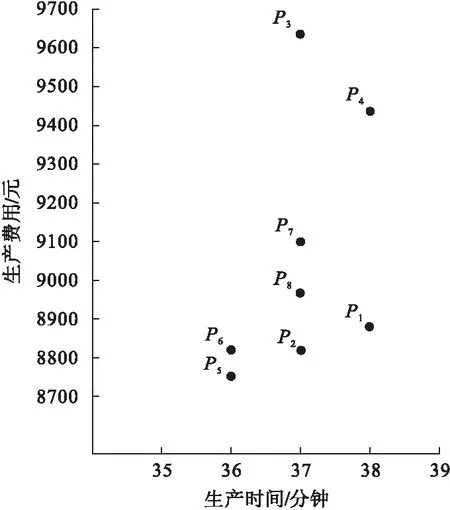
图2 遗传产生的后代
通过示意图2可以清楚的看到,P5点的个体在图的最内侧,即其横坐标和纵坐标都小于其它个体的横纵坐标,故可将P5点定级为0级。很显然,其它个体的级别都大于P5点,生产周期和生产费用也大于P5点,所以最终得出的最优解是生产周期36分钟,生产费用为8750元。通过仿真得到的最优甘特图如图3所示。
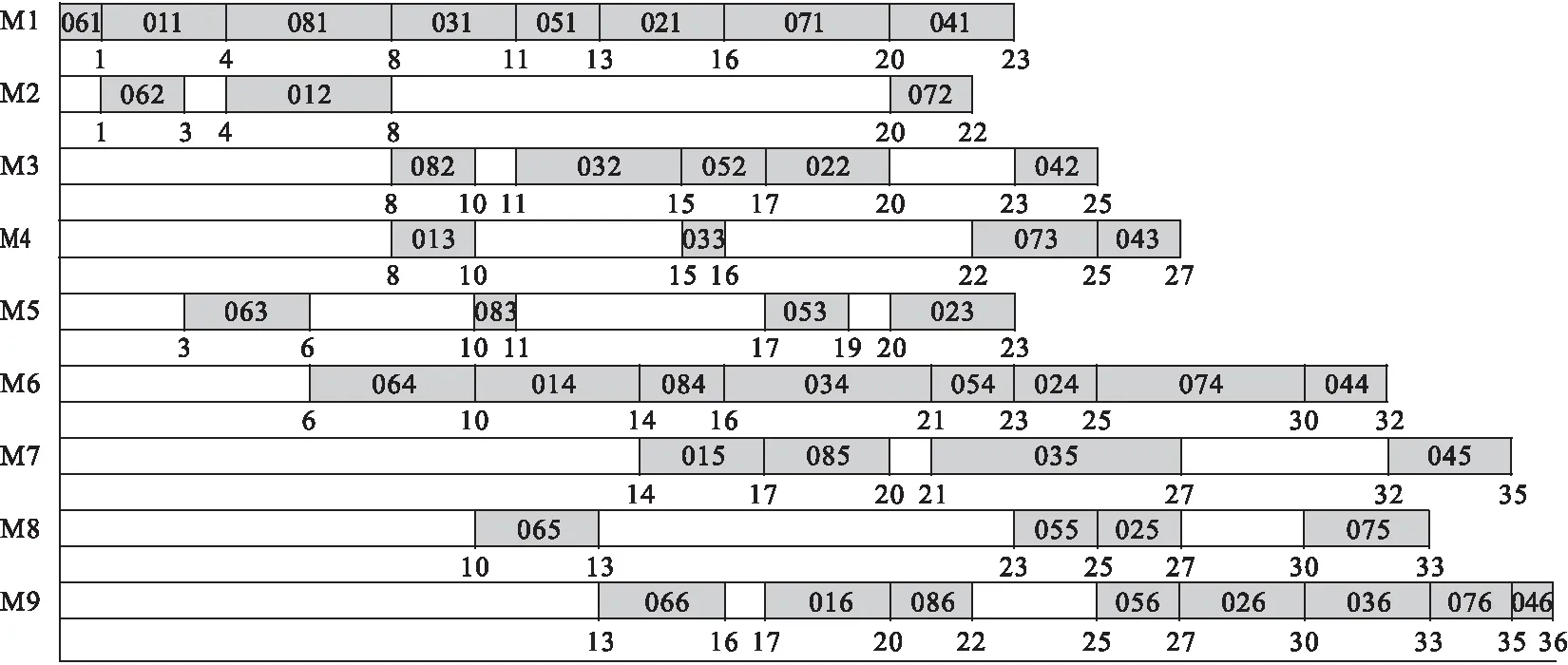
图3 双目标混合流水车间调度甘特图
从图3上可以看出工件在并行机器上的分配情况,且工件的具体加工顺序和加工时间均已确定。本文运用小生境遗传算法解决HFSP问题,充分缩短了加工时间,减少了生产费用,提高了车间的生产效率。
5 结论
针对遗传算法解决双目标混合流水车间调度问题的不足,提出了将小生境算法与遗传算法结合的方法,既保持了种群的多样性,又可提高全局的搜索能力和收敛速度,从而找出更多的最优解以供选择。解决了双目标混合流水车间调度的核心问题,即工件在每个机器上的分配问题、各机器工件上的加工顺序问题以及平衡双目标之间的冲突而选取最优结果问题。运用此方法得到的是一组最优解集而并非是单个的最优解,是直接对两个目标进行同时处理,结果更加切合实际。通过合理的参数设计建立仿真模型,仿真结果证明该方法的可行性和有效性。
——以贵阳花溪公园为例

