基于压缩感知的ACNS碰撞信息重构方法

陆 颖 张玉辰 刘 琰 谢君平

1(江苏大学汽车与交通工程学院 江苏 镇江 212000)2(陆军军事交通学院镇江校区 江苏 镇江 212000)

0 引 言

ACNS[1-3]是一种事故后安全技术，能够在车辆发生严重碰撞后自动地对外发出求救信号，从而有效地缩短救援时间、提高救援效率。目前，大多数ACNS以安全气囊点火信号作为触发信号源，即系统中的事故检测模块一旦检测到安全气囊点火，就自动触发呼救模块。但是，这种类型的ACNS的可靠性受到安全气囊系统制造质量的制约，而且对于那些出厂时未装备ACNS的车辆来说，要想后期加装这种类型的ACNS需要对安全气囊系统进行改造，具有极高的技术难度和极大的安全风险。基于此，近年来国内外加大了非安全气囊点火信号触发的ACNS的研发力度，目前以车身加速度信号触发的ACNS是研究的热点。其工作原理是：事故检测模块实时采集车身加速度信号，通过事故检测算法识别碰撞是否发生以及事故的严重程度，并决定是否对外呼救。如果检测到碰撞事故发生且需要对外呼救，ACNS终端通过呼救模块向救援中心发出求救信号及事故信息。

碰撞加速度对于判断事故严重性等级和预测乘员伤情具有重要意义，也是事故分析、司法鉴定、车辆质量评定的重要依据。目前，碰撞加速度可以通过安装在车辆前端两侧、前端中央、车身左右侧等位置的加速度传感器获得。这些加速度信号主要是输入到安全气囊控制器，用来判断安全气囊是否需要打开，外接设备很难直接读取这些数据。此外，对于一些配备事故数据记录仪(Event Data Recorder，EDR)的车辆来说，EDR能够自动记录和存储车辆发生碰撞事故时的加速度数据，但是这些数据必须由4S店或企业的售后团队通过专门的解码软件解码后才能看到。根据GB7258-2017，交通管理部门虽然提出未来将要求新生产的乘用车上配备EDR，但全面铺开仍需时日。基于此，以车身加速度信号触发的ACNS中的事故检测模块如能存储并利用呼救模块对外发出碰撞时的车身加速度数据，使得其具有部分EDR的功能，将极大提高这种类型ACNS的实用性和推广价值。

对于ACNS而言，需要在较短的时间内完成判断-呼救等一系列工作，尤其在严重碰撞事故发生后，由于车辆电源的损坏，将只能利用ACNS自身的备用电池，这就要求ACNS能够在最短的时间内以最小的数据量实现最大限度的加速度数据存储。压缩感知(Compressive Sensing，CS)[4-6]是一种新的采样模式，在采集的过程中，就开始对数据进行压缩，而且这种压缩又能保证信号的低失真甚至不失真，再恢复原始数据，就可以降低采集信号的计算量和存储空间。目前，CS理论在医疗成像、模式识别以及图像处理等方面得到了广泛应用。由于CS技术主要应用于稀疏信号或可压缩信号，碰撞加速度信号使用CS技术的压缩和还原效果如何是一个值得研究的问题。

本文探讨压缩感知在ACNS中的应用流程，通过台车碰撞试验获得20 km/h下的加速度信号。然后，基于正交匹配追踪算法，利用离散余弦变换矩阵和高斯随机观测矩阵，选定合适的观测值,对碰撞加速度信号进行压缩重构，实现加速度信号高精度还原，使得碰撞事故发生后加速度数据更快速的传输。

1 压缩感知理论

CS理论的原理是：将信号的采样、压缩和编码集中在一个环节，信号经过线性观测得到M个观测值，在一定条件下，根据M个观测值，运用重构算法准确地还原信号。

1.1 稀疏性

CS理论的前提是信号是稀疏的或可压缩的。当信号中非零个数K远小于维数N时，便认为是稀疏的，称作K-稀疏信号，稀疏信号是可以压缩的。一般情况下信号本身不是稀疏的，但可以选取合理的稀疏变换矩阵通过某种变换表示为稀疏信号，即原始信号x可通过稀疏变换矩阵Ψ表示：

x=Ψs

(1)

式中：x为一个N×1向量，即x=[x1,x2,…,xN]T；Ψ为N×N矩阵；s是将x进行稀疏表示的变换系数，为N×1向量，其中大部分元素值为0。x在Ψ上只有K个非零元素，便认为信号可稀疏表示。非零元素个数越少，表示信号越稀疏。s经排序后呈指数衰减趋于零，也可认为信号x可稀疏表示。

稀疏表示的原理就是通过线性空间映射，将信号在稀疏空间进行表示[7]。常用的处理一维信号的稀疏变换有傅里叶变换、小波变换和离散余弦变换等。

1.2 观测系统

观测矩阵的选取对能否完成信号重构以及重构的质量有着决定性作用，合适的观测矩阵可保证在变换和逆变换过程中一些重要的数据不会丢失，从而保证信号准确重构。将x向一个观测矩阵Φ投影，得到观测向量y，表示为:

y=Φx

(2)

式中：Φ是一个M×N的矩阵，并且M≪N，代入式(1)得到：

y=ΦΨs=Θs

(3)

式中：Θ=ΦΨ为M×N维传感矩阵。观测矩阵Φ要与稀疏变换矩阵ψ不相关，即不能由ψ稀疏表示，同时观测矩阵Φ必须满足有限等距性质(Restricted Isometry Property,RIP)。RIP是保证信号能够重构的充分条件[8]。CS中常用到的观测矩阵有高斯随机矩阵和贝努力随机矩阵等。高斯随机矩阵中，矩阵内的每个元数都是随机的，对于一维信号，满足与大多数正交变换矩阵不相关[9]，在M≤O(KlogN)[10]条件下，也能很大概率满足RIP性质[11]。

1.3 重构算法

对原始信号测量编码后，需要通过y重构出x，理论证明可以通过求解最小范数l0来重构原始信号x：

(4)

这里要求s中l0最小范数即非0值个数最小，由于M≪N，通过y重构出x是一个欠定方程，可以有无数个解，因此信号的重构是一个NP难问题。

由于 l0最小范数优化问题很难解决，进而研究通过求解l1最小范数来求解次优解，而l1最小范数的求解是易解决的。基于l1求最小范数的重构算法有基追踪(Basis Pursuit，BP)算法、迭代阈值(Iterative Thresholding，IT)法和梯度追踪(Gradient Pursuit，GP)法等，但这类算法计算较为复杂，重构速度慢。

贪婪算法虽是针对求l0最小范数问题的一种重构算法，但通过在每次迭代中选取局部最优解来重构原始信号，允许一些重构误差。该类算法主要包括匹配追踪(Matching Pursuit,MP)算法、正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法和规整化正交匹配追踪(Regularized Orthogonal Matching Pursuit,ROMP)算法等[12]。

MP算法简单易懂，是基本的重构算法，其主要思路是在进行迭代的同时，会在测量矩阵进行优化筛选，筛选出最匹配的元素来描述对应的原始信号的特征，这就使得信号间的误差尽量最小化。但因原始信号和观测矩阵中的元素不能够完全相互独立正交，匹配的过程将会很长。在此基础上提出的OMP算法能够有效克服MP算法中的不足，能够将选定的集合正交化，正交化的集合在匹配原则上满足迭代的最优化要求，同时相对于MP算法能够减少迭代的次数，迭代次数与输入密切相关，运算的时间会随着采样个数的增多而增加，计算量也会增加。ROMP算法在OMP算法的基础增加了规整化的步骤，使得重构过程更加均衡稳定，运算时间与OMP算法差不多，但计算复杂度较高，相比之下，OMP算法更容易操作和实现。

2 ACNS终端设计

ACNS终端框图如图1所示，实物如图2所示。ACNS终端以STM32F407ZGT6芯片为核心，内置三轴加速度传感器，外接GPS模块和GSM模块。加速度传感器用于实时采集车身加速度信号；GPS模块用于接收地理位置信息；微控制器收集加速度传感器、GPS模块的数据，在判断车辆发生碰撞后，将相关信息整合发送至GSM模块，由GSM模块负责将事故信息发送出去；SD卡用于存储微控制器处理后的碰撞初速度、碰撞过程中的加速度等数据；显示屏用于显示碰撞时的地理位置、碰撞初速度等事故信息；锂电池为整个终端供电。

图2 ACNS开发板实物图

将压缩感知理论运用于ACNS终端，其压缩-还原的流程如图3所示。碰撞发生后，加速度传感器将采集到的碰撞加速度信号进行稀疏变换；然后通过观测矩阵将经过稀疏变换后的信号线性投影得到M个观测值，即M维观测向量，GSM模块将观测向量发送至呼救中心；最后通过重构算法还原出原始信号。原始信号在压缩后，信号波的数据量的大小变得很小，有利于信息的快速传输，减轻了内存空间的压力。

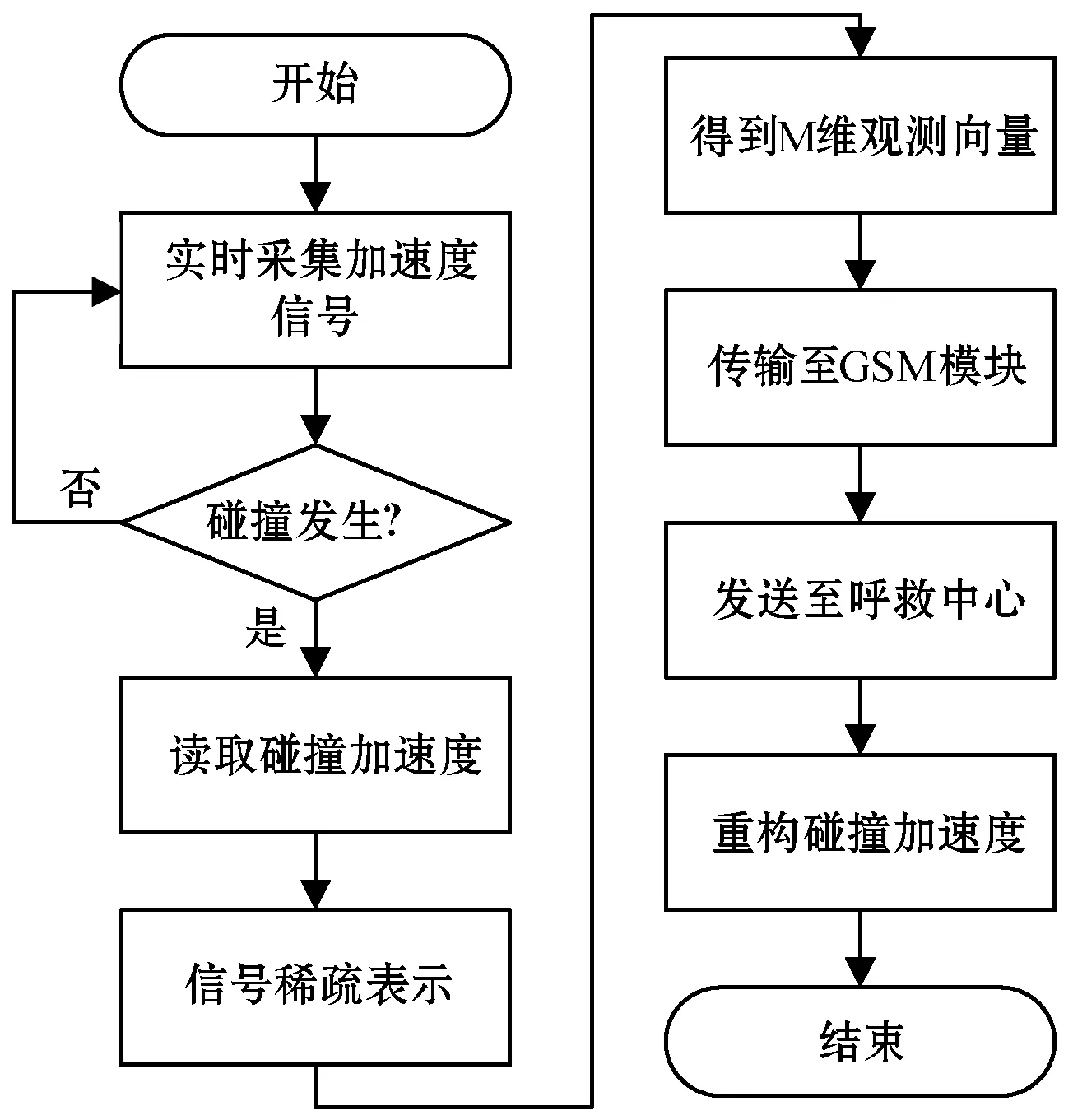
图3 压缩感知处理过程

压缩感知在信息采集和传输方面的优越性，且能够通过重构算法高度还原出原始信号，保证了信息的可靠性，给救援人员提供有效的信息，帮助其采取相应的救援方案，有望成为提高救援效率的途径之一。

3 加速度信号处理与仿真

3.1 加速度信号预处理

参考欧洲ECE R94对安全气囊的点火要求，车辆以大于30 km/h速度正面碰撞固定壁障时，安全气囊必须点火，低于20 km/h不应点火，20～30 km/h之间不作要求[13]，因此将20 km/h作为ACNS触发的临界车速。通过台车模拟碰撞试验获取20 km/h下的碰撞加速度数据，所用台车试验系统为DAPG-QJ-MNPZ，如图4所示。台车在碰撞初始阶段受到来自其他方向的力，会使得碰撞开始时加速度信号有明显的大幅度振荡。在碰撞过程中加速度信号变化非常快，容易受到台车振动和轨道不平的干扰。故要对加速度信号先进行滤波处理，除去这些干扰。在滤波之前，对原数据进行波形化处理，根据产生的波形选取有代表性的部分。本文利用MATLAB软件进行滤波，滤波处理中数据的采样频率为1 000 Hz，滤波频率为60 Hz，滤波阶数为108。碰撞加速度信号处理结果如图5所示。

图4 台车试验系统

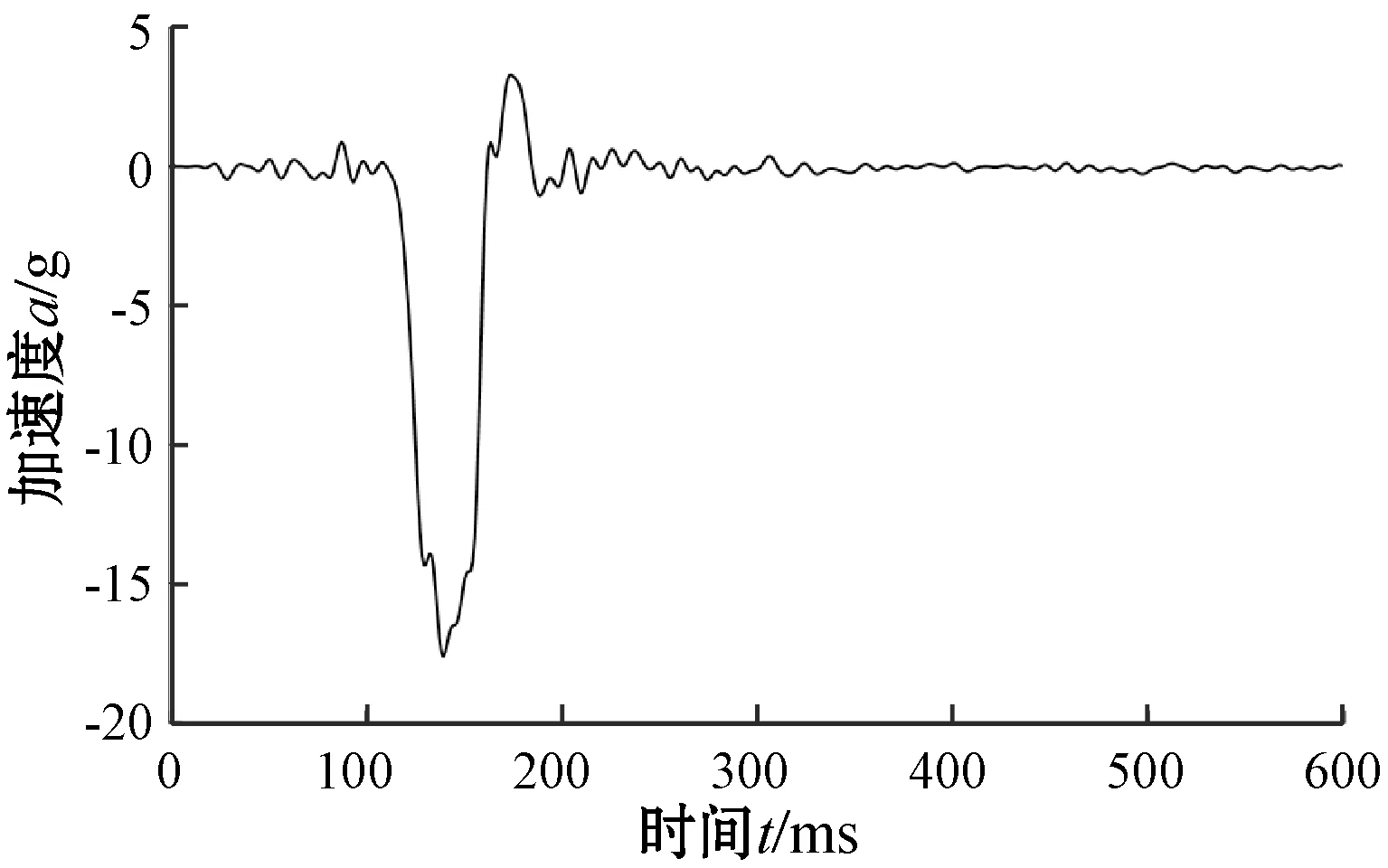
图5 台车20 km/h的碰撞加速度曲线

3.2 加速度信号压缩还原实验及分析

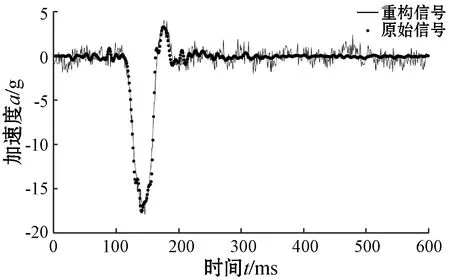
加速度信号为一维信号，取信号长度N=600，基于OMP重构算法，利用离散余弦变换矩阵和高斯随机观测矩阵，对加速度信号进行压缩还原。观测值M=200和M=280时，在MATLAB软件中得到的重构信号与原始信号的对比如图6、图7所示。

(a) 时域对比

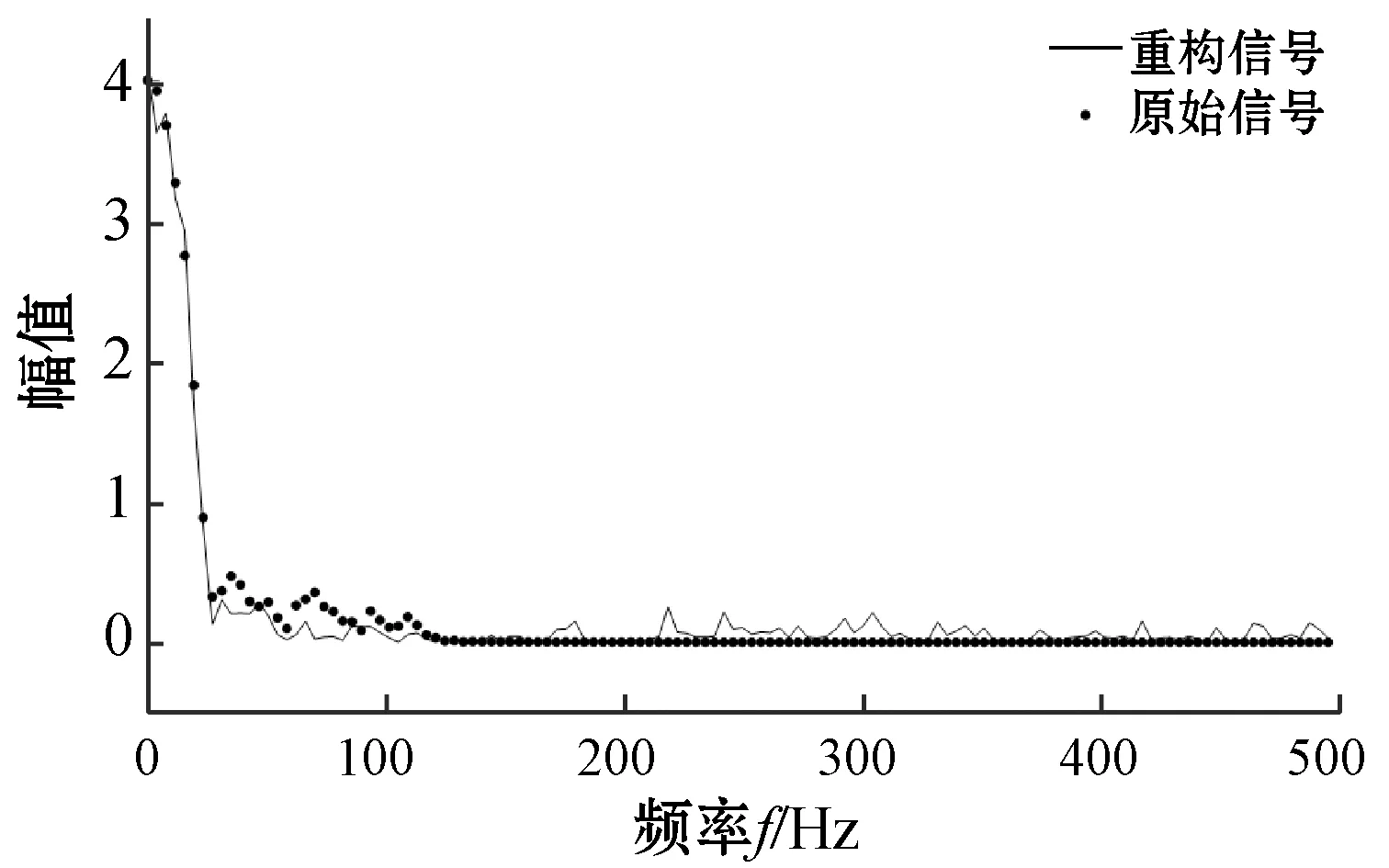
(b) 频域对比图6 M=200时的重构信号与原始信号对比

(a) 时域对比

(b) 频域对比图7 M=280时的重构信号与原始信号对比

比较图6和图7可以看出，随着M的增大，加速度信号重构的质量越来越好，重构出来的波形更接近原始信号波形。

图6中，重构出的加速度信号波与原始信号波相差较大，偏移原始信号的点较多，整体波形较密集，只是在正负上能看出有一致性。虽然波峰未能达到预期的效果，但是可以看出原始信号和重构信号的波形趋势一致，这表明还原是无限逼近原始信号的。在频域中波形的幅值有一定的差距，由于观测值的选择，幅值方面还有些欠缺。

图7中，时域信息和频域信息得到很好的还原，重构出来的波能够识别出正负交替变换的趋势，波形基本相同，在频域中幅值近乎一致，重构出来的信号非常接近原始信号。但随着M的增大，算法迭代次数增加，计算出的迭代值也会增多，必将增大计算量。

加速度信号重构的相对误差Error计算公式为：

(5)

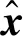
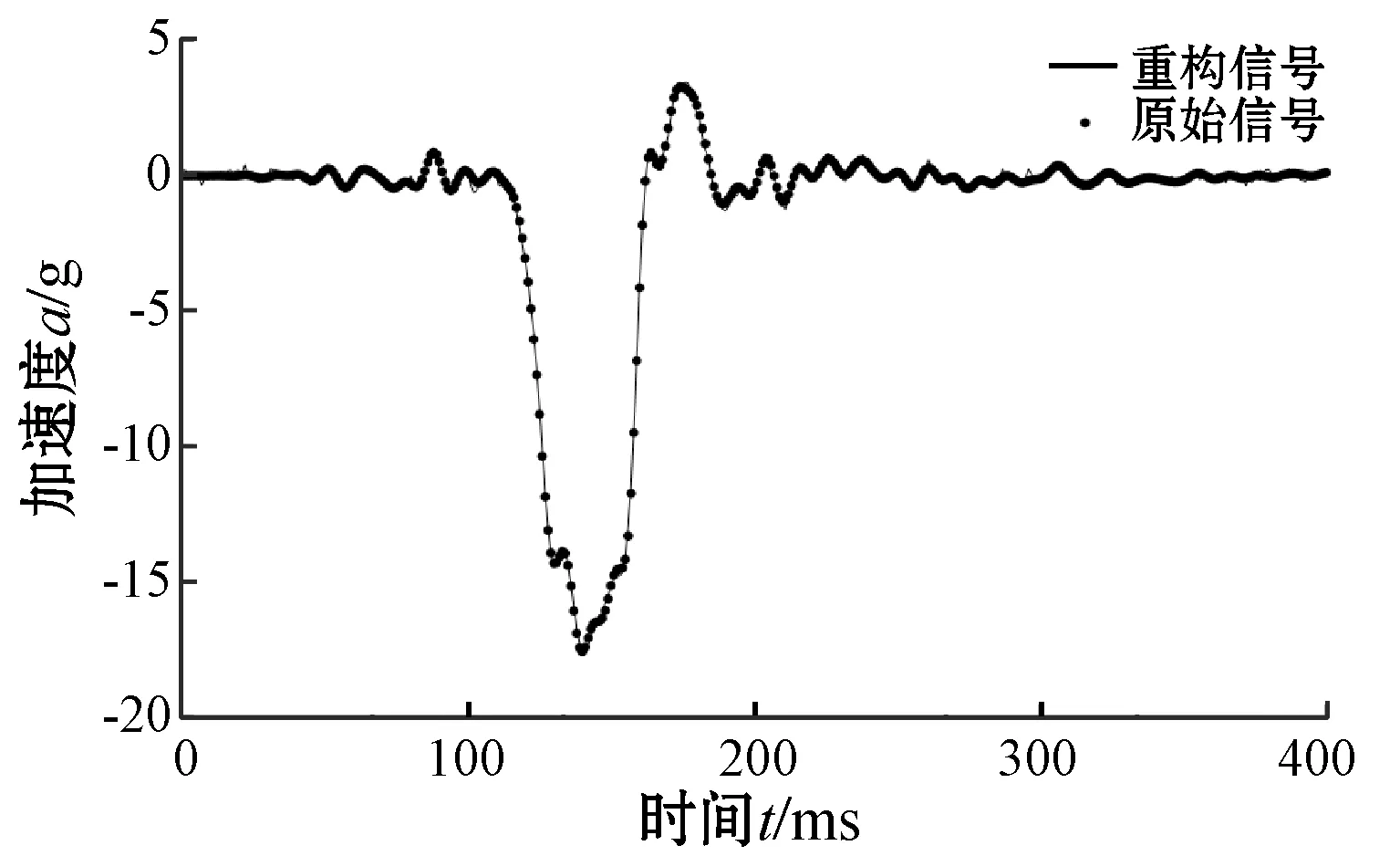
(a) 时域对比

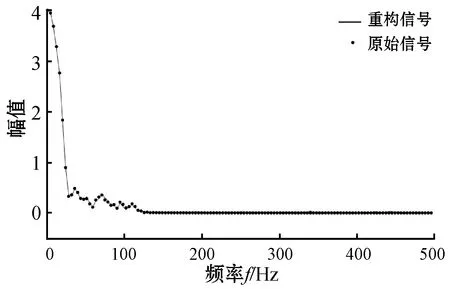
(b) 频域对比图8 N=400时的重构信号与原始信号对比(M=190)

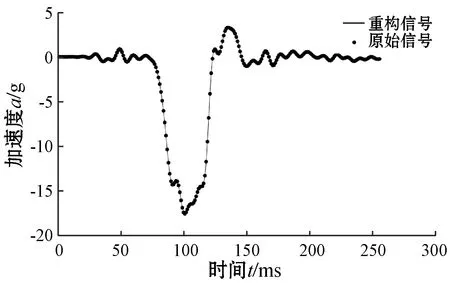
(a) 时域对比

由图8和图9可以看出，N为400和256时，时域信息和频域信息同样能够很好地还原。最大波峰值同样能够获得，说明加速度信号在压缩重构后，加速度信号的最大值、波形的最大波峰值不会失真。N=400和N=256时，Error分别为0.036 0、0.003 5，说明缩短信号长度，选择合适的M值后，重构误差明显降低。

通过对比图6-图9中原始信号和重构信号的波形可知，选取合适的观测值能够较为准确地重构出碰撞加速度信号，并且本次实验所得误差较小，数值较为理想。由此可见，将压缩感知理论运用于ACNS碰撞加速度信号传输具有可行性。

4 结 语

本文将压缩感知应用到ACNS碰撞加速度信号传输中。 基于STM32F4系列开发板设计了ACNS终端，并介绍了压缩感知应用于ACNS碰撞加速度信号压缩还原的流程。利用台车碰撞试验获取20 km/h下的碰撞加速度信号并进行了滤波处理。基于 OMP重构算法，利用离散余弦稀疏变换矩阵和高斯随机观测矩阵，对加速度信号进行压缩重构。结果表明，选取合适的观测值时，信号重构效果较好，所得误差也较小，能够较为准确地还原碰撞加速度数据。因此，将压缩感知运用于ACNS对加速度信号进行压缩传输和还原读取具有可行性。