复合材料层合板固化过程多物理场耦合数值模拟

(1.兰州理工大学 材料科学与工程学院，甘肃 兰州 730050； 2.兰州理工大学 理学院，甘肃 兰州 730050)

1 引 言

热压罐成型工艺是制造连续纤维增强热固性树脂基复合材料构件的主要方法。由于影响构件成型质量的因素较多，而且实验周期长、成本高，难以保证重复性。在这种情况下，采用数值模拟法建立一种比较完整的固化过程分析和预测模型尤为重要。

近二十几年来，国内外众多学者针对复合材料固化过程进行了数值模拟研究。初期，对层合板固化的数值模拟多采用简单的一维和二维模型[1-3]。随着计算机技术的不断进步，一些学者建立了复合材料固化的三维有限元分析模型[4-6]，实现了对复杂结构件固化的模拟研究。对复合材料固化过程中温度场变化情况的研究较多[7]，少数学者还实现了复合材料固化的多物理场耦合计算[8-9]。

能否准确预测固化过程残余应力的关键在于选择合适的本构模型。在早期的研究中，弹性模型的运用较多，将其与经典层合板理论结合可以较好地预测薄板的残余应力[10-12]。但是，弹性模型仅仅考虑的是冷却阶段残余应力的发展状况，忽略了冷却前产生的应力。众所周知，树脂在固化过程中会发生明显的粘弹性性能的变化，尤其在升温和保温阶段，这也引发了许多学者对粘弹性模型的青睐。由于粘弹性模型自身的复杂性，在研究初期，人们只是利用粘弹性模型预测冷却阶段的固化残余应力[13]。后来，引入时间-温度叠加原理和等效原理，将材料的热膨胀、化学收缩和应力松弛等因素考虑在内，使得对固化残余应力发展变化的预测研究更加深入[14]。

本研究建立了层合板固化的三维有限元分析模型，考虑了材料性能在固化过程中的时变特性，并采用COMSOL多物理场耦合分析软件对层合板固化过程中的温度场、固化度场及残余应力场进行耦合计算分析。

2 数学模型

2.1 热化学模型

热化学模型由热传导方程和固化动力学方程构成，可以用来计算复合材料固化过程中的温度场和固化度场。复合材料固化过程中的热量主要来源于两个方面，一是经模具辅助材料传递给复合材料结构的外界热量，另一部分是树脂基体固化过程中化学反应产生的非线性内热源。对于内热源的热传导问题，本研究采用Fourier热传导定律和能量平衡关系来建立数学模型。三维瞬态热传导控制方程为[2]：

(1)

式中：ρ、Cp、T和t分别为复合材料的密度、比热、温度和时间；kx、ky和kz分别为复合材料在x、y和z方向上的导热系数；Q为内部热源，由下式确定：

(2)

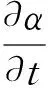
树脂基体的固化反应是一个热激活的复杂的化学交联反应，因此大多数有关固化反应动力学的方程建立在经验模型基础上。本研究采用唯象动力学模型，该模型不考虑整个反应过程中的动力学机理，只用简单的公式来表示反应中各参数的相互作用关系。本研究主要采用3501-6环氧树脂对所建模型进行验证，其固化动力学方程为[1-2]：

(3)

其中，Ki(i=1,2,3)为反应速率常数，由下式确定：

(4)

式中：Ai、Ei和R分别为频率因子、活化能和普适气体常数。在实际计算中，由于不能计算零的负整数次幂，因此初始条件可设为α|t=0=10-10。3501-6环氧树脂的固化动力学参数如表1所示。

表1 3501-6 环氧树脂的固化动力学参数[1-2]Table 1 Cure kinetic parameters of 3501-6 epoxy resin [1-2]

2.2 粘弹性力学模型

尽管粘弹性模型存在一些局限性，例如：对材料实验数据需求量大，占用计算机内存，计算时间长等，但是它是描述热固性树脂基复合材料固化过程中粘弹性行为最精准的数值计算方法之一。假设层合板在固化发生前无应变产生，则粘弹性材料的应力可以由下式确定[15]：

(5)

其中，

εtc=εth+εch=φΔT+φΔα

(6)

式中，C为松弛刚度矩阵，其分量的计算方法参见文献[3]；εtot和εtc分别为总应变和热化学应变，热化学应变包括热膨胀应变εth和化学收缩应变εch；φ和φ分别为热膨胀系数和化学收缩系数；ξ(t)和ξ(τ) 分别表示当前和过去相对时间，由式(7)确定：

(7)

式中：αref为参考固化度；aT为移位因子。根据n单元并联的广义麦克斯韦模型，粘弹性复合材料的松弛模量可以表达为[2]：

(8)

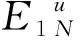
(9)

2.3 材料热物理性能

在固化过程中，复合材料及其组份的热物理参数(包括密度、比热容和导热系数)是随温度和固化度的变化而变化的。

AS4碳纤维的密度为常量1790kg·m-3，3501-6环氧树脂的密度由式(10)计算得到[2]：

(10)

表3 AS4/3501-6复合材料组份的弹性力学性能[3]Table 3 Elastic mechanical properties of AS4/3501-6 composite constituents [3]

AS4/3501-6复合材料的密度可以用混合率公式计算如下[15]：

ρ=vfρf+(1-vf)ρr

(11)

式中，ρf为纤维的密度。

AS4碳纤维的比热容与温度呈线性关系[2]：

Cpf=1390+4.50T

(12)

3501-6环氧树脂的比热容是温度和固化度的线性函数[2]：

Cpr=4184[0.468+5.975×10-4T-0.141α]

(13)

AS4/3501-6复合材料的比热容用混合率公式计算[15]：

(14)

AS4碳纤维的导热系数是温度的线性函数[2]：

kf=0.742+9.02×10-4T

(15)

3501-6环氧树脂的导热系数是温度和固化度的线性函数[2]：

kr=0.04184[3.85+(0.035T-0.141)α]

(16)

复合材料的导热系数具有各向异性，复合材料平行于纤维方向和垂直于纤维方向的导热系数可以用混合率公式计算得到[15]：

kL=vfkf+(1-vf)kr

(17)

(18)

其中，

(19)

3 基于COMSOL的数值模拟算法

在第2节中提出的理论模型基础上，运用COMSOL 多物理场耦合有限元分析软件(4.3b版)对纤维增强树脂基复合材料层合板的固化过程进行数值模拟分析。理论模型包含两部分：热化学模型和粘弹性力学模型。热化学模型由热传导和固化反应动力学组成。模型之间存在着一定的耦合关系，它们之间的耦合计算可通过COMSOL软件中相应的应用模块来实现，具体的模拟流程图见图1。

图1 复合材料固化过程数值模拟程序流程图Fig.1 Flow diagram of numerical simulation procedure during cure cycle for composite

首先，利用软件中的“热传递”应用模块模拟热传导模型。在模块中输入材料的初始温度、固化工艺参数及热物理性能参数，同时调用第二个模块(固化反应动力学模块)中计算得到的固化度值，通过计算式(1)得到固化温度分布。

其次，利用软件中的“系数型偏微分方程”应用模块模拟固化动力学模型。系数型偏微分方程的形式为：

β·u+au

(20)

式中，u和t分别为因变量和瞬态时间；c，a，ea，da，α，β和γ均为待定系数；f是源项。经过设定系数和源项，将式(20)转化为式(3)的形式，输入初始固化度和固化动力学参数(见表1)，并调用由热传递模块计算的温度分布，得到材料的固化度分布。

最后，利用软件“结构力学”应用模块中的“粘弹性材料”项模拟粘弹性力学模型。在该项中输入边界载荷、松弛因子、松弛时间(见表2)及弹性力学性能参数(见表3)，并调用由“热传递”模块和“系数型偏微分方程”模块计算的温度分布和固化度分布，得到层合板的弹性模量变化情况和固化残余应力分布。

整个耦合过程在每一个时间增量内反复迭代求解，直到达到所要求的精度，整个循环过程一直作用到固化完成。上述过程中计算得到的新的状态参数有材料密度、比热容、导热系数、热膨胀系数和模量等，在下一个时间增量内进行耦合求解时，需要更新这些状态参数。

4 算例验证

为了验证所构建模型的有效性和准确性，构造了一个正交各向异性四层复合材料层合板，铺层顺序为[0°/90°/90°/0°]，尺寸为10.16×10.16× 2.54cm，如图2所示。材料选为碳纤维增强环氧树脂预浸料AS4/3501-6，AS4碳纤维被视为横向同性材料，因此，横向各方向性能参数相同，3501-6环氧树脂和AS4碳纤维的力学性能参数如表3所示。网格的划分直接影响着数值模拟的收敛性和准确度，本研究通过有效网格验证，选取了最佳网格，即采用六面体单元划分网格，其离散的单元总数为9216，如图3所示。

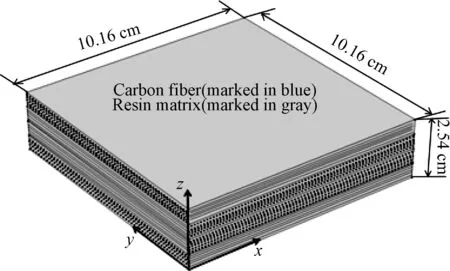
图2 复合材料层合板几何模型Fig.2 Schematic of the composite laminates

实验采用的固化工艺如图4中的短横虚线所示，包括五个阶段，在第一加热阶段，以2.5℃/min的速率从25℃升温至 116℃，保温1h后再次以2.5℃/min的速率加热至177℃，随后进入第二保温阶段，保温2h，以-2.5℃/min的速率冷却至25℃。在模具与构件的界面上设置了两个边界条件：热量和压力(见图3)，在层合板的外表面设置模具加热的固化工艺(见图4)，在侧面和底面施加压力为689kPa。

5 分析与讨论

5.1 热化学分析

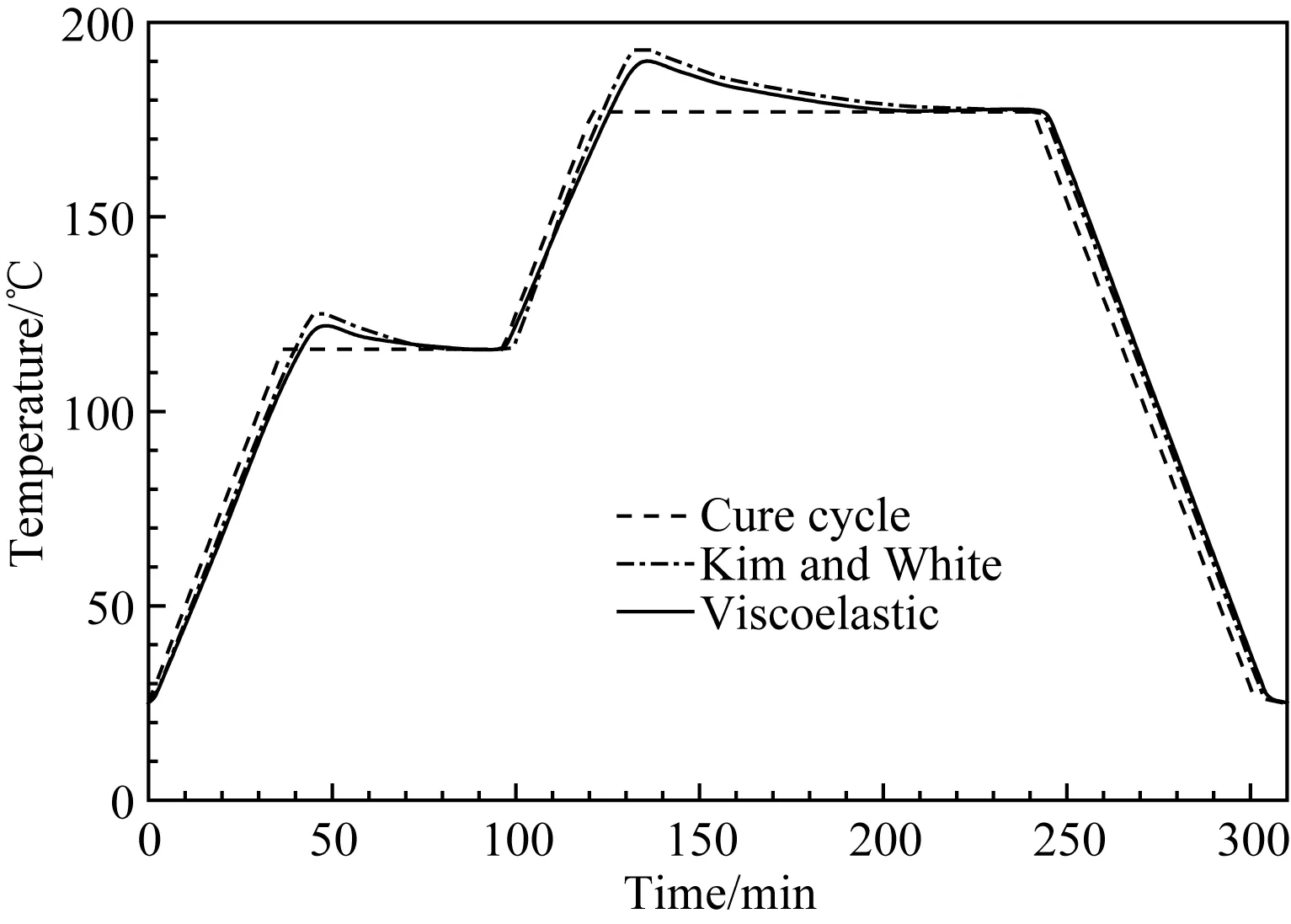
图4 复合材料层合板中心点(5.08, 5.08, 1.27)的温度变化情况Fig.4 Development of temperature in central point (5.08, 5.08, 1.27) of the composite laminate under manufacture recommended cure cycle

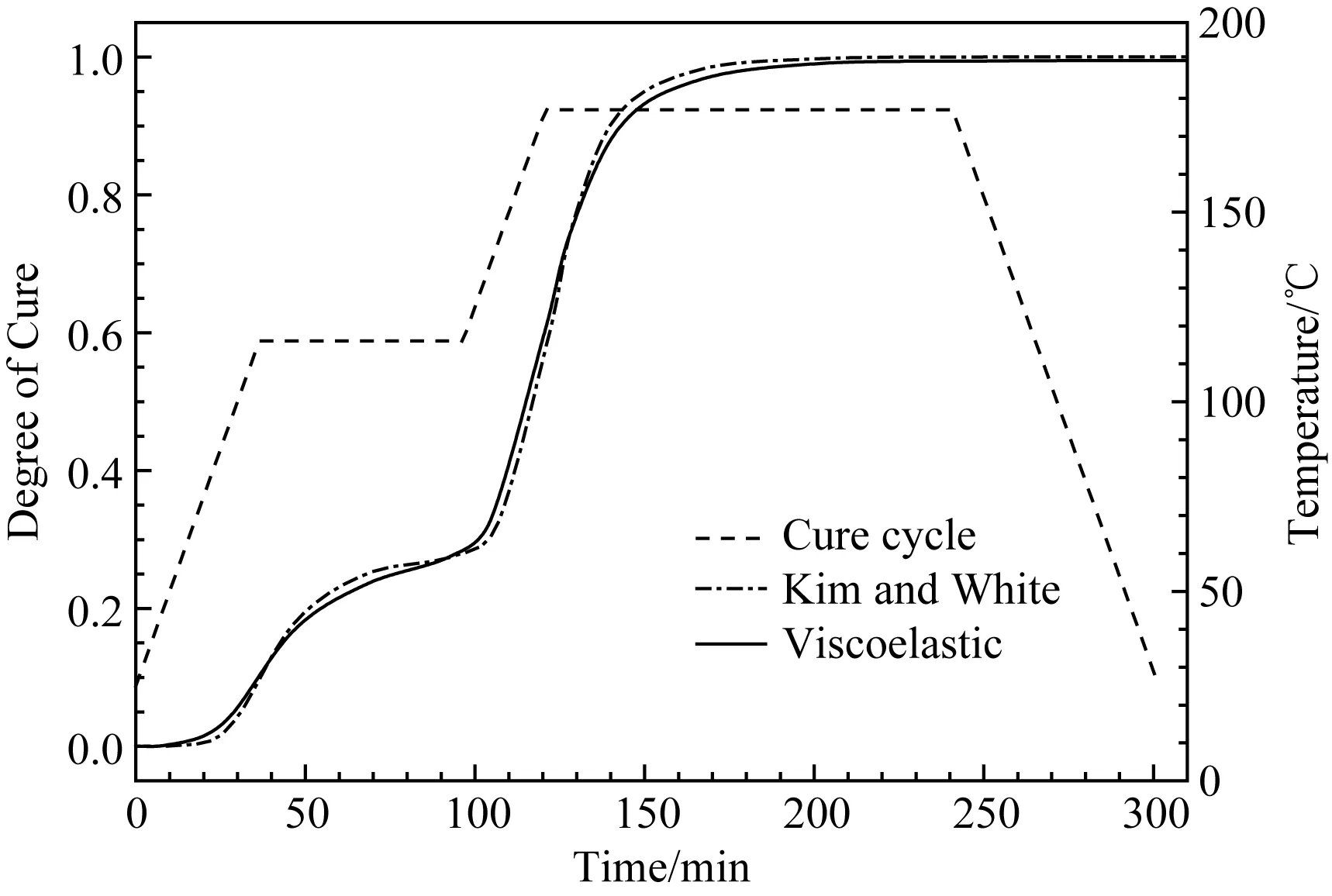
图5 复合材料层合板中心点(5.08, 5.08, 1.27)的固化度变化情况Fig.5 Development of DOC in central point (5.08, 5.08, 1.27) of the composite laminate under manufacture recommended cure cycle

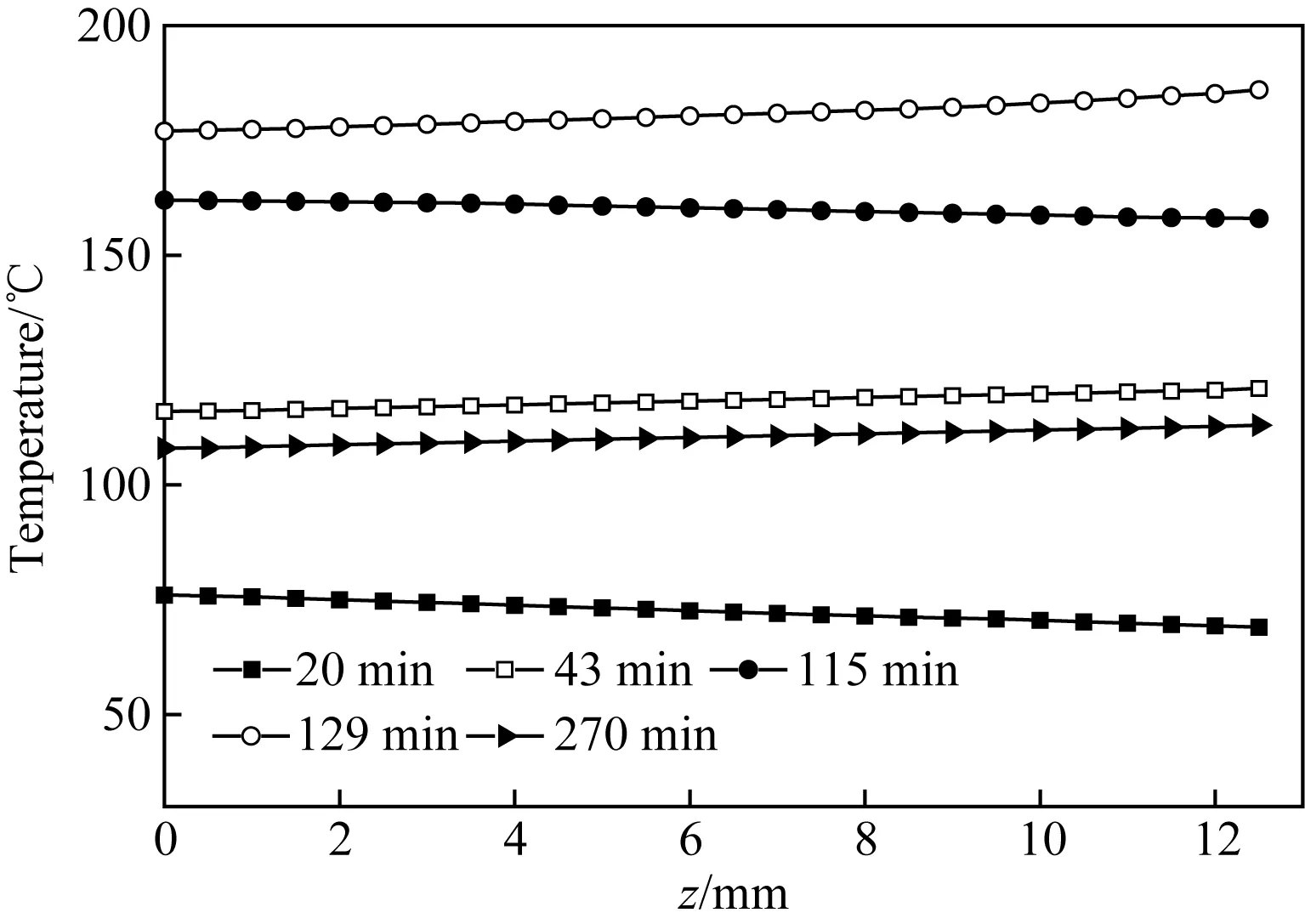
图6 复合材料层合板表面点(5.08, 5.08, 0)到中心点(5.08, 5.08, 1.27)直线段上温度变化情况Fig.6 Development of temperature on a line from surface point (5.08, 5.08, 0) to central point (5.08, 5.08, 1.27) of the composite laminate

图4和图5为固化过程中层合板中心点(5.08, 5.08, 1.27)的温度和固化度变化情况。结合图6中关于层合板厚度方向上温度变化情况的数值计算结果进行固化的热化学分析。在第一升温阶段，由于外部先受热，而内部树脂尚未发生剧烈反应，所以，层合板的中心温度低于环境温度。在接下来的保温阶段，由于外部热量向层合板内部传递，再加上化学反应放热的不断积累，中心温度迅速上升，并在43min时达到第一个峰值121℃。在第二升温阶段，由于复合材料较低的导热系数和热传导滞后，层合板中心温度再次低于环境温度，但交联反应更加剧烈。进入第二保温阶段后，随着热传导和内部固化放热的积累，高温区域再次向内部转移，并在129min时达到第二峰值191℃。最后，在冷却阶段，随着固化反应基本完成，固化放热减少，中心温度渐渐接近室温。从图4和图5可见，本研究模型关于材料固化温度和固化度的计算结果与Kim 和 White[3]的研究结果基本一致。由于本研究模型考虑了材料热物理性能随固化温度和固化度变化的特性，计算出的固化过程中层合板中心温度在第一和第二保温阶段的峰值分别比文献计算结果小2.3%和2.5%，固化反应开始时间提前了10min左右，而最终固化度值降低了约0.01。

5.2 力学分析

图7和图8分别为层合板中心点(5.08, 5.08, 1.27)厚度方向弹性模量和剪切模量随时间的变化情况。从图可见，弹性模量和剪切模量均随固化度产生非线性变化。在第一升温和保温阶段，树脂还未发生剧烈反应，处于粘流态，模量很小，几乎不发生变化；到了第二升温阶段，随着固化反应的剧烈进行，模量迅速增大；约从180min开始，随着固化反应减弱，模量的变化速率明显降低，直至冷却结束。

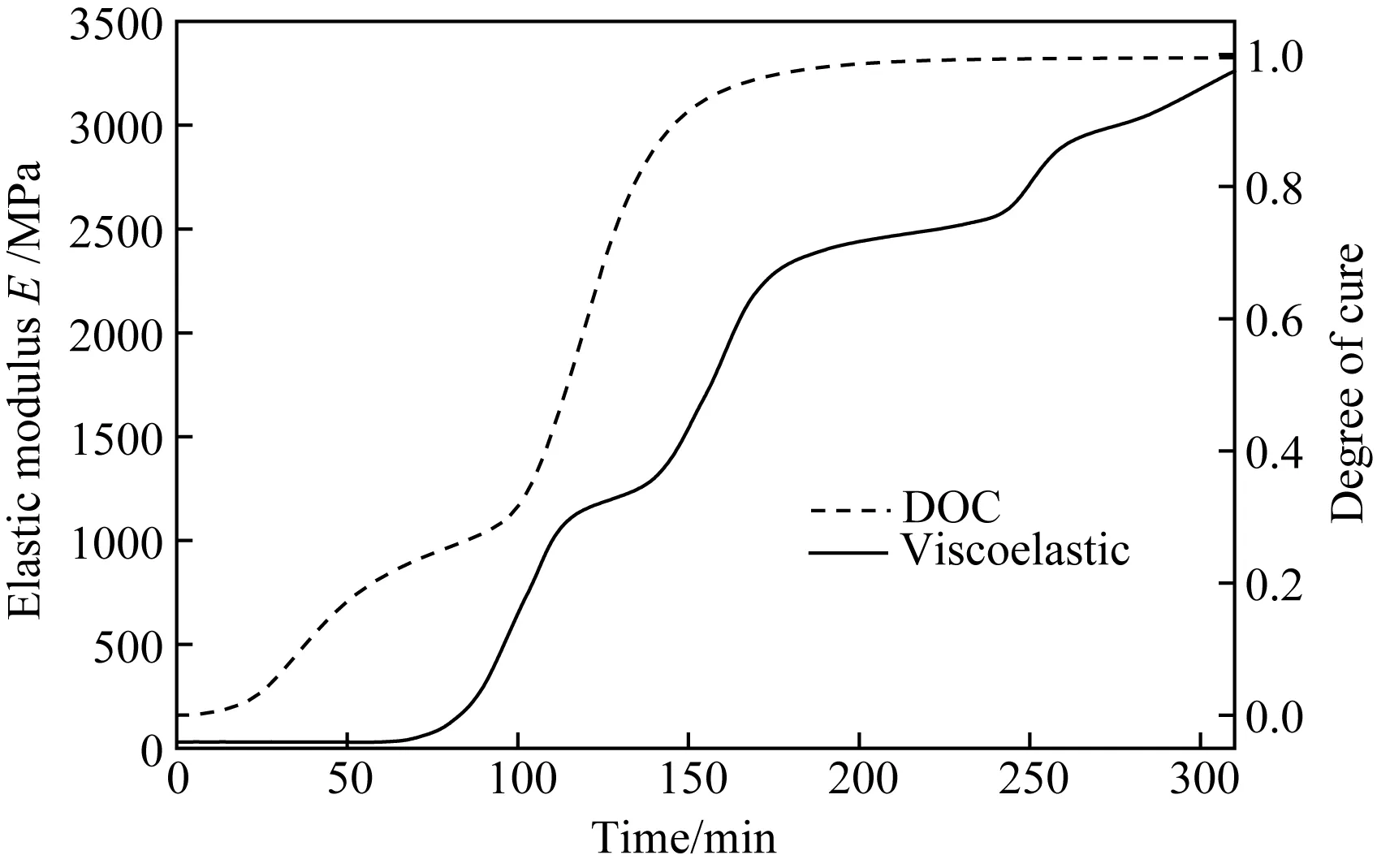
图7 复合材料层合板中心点(5.08, 5.08, 1.27)厚度方向弹性模量变化情况Fig.7 Development of elastic modulus in through-thickness direction in central point (5.08, 5.08, 1.27) of the composite laminate under manufacture recommended cure cycle

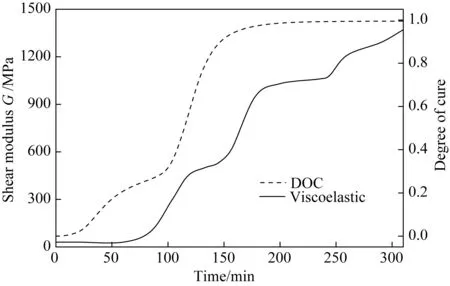
图8 复合材料层合板中心点(5.08, 5.08, 1.27)剪切模量变化情况Fig.8 Development of shear modulus in central point (5.08, 5.08, 1.27) of the composite laminate under manufacture recommended cure cycle

图9和图10分别为层合板在点(5.08，0，1.27)处的层间正应力σ3和0°层中点(5.08，5.08，2.22)处垂直于纤维的横应力σ2随时间的变化情况。从两图均可看出，在开始阶段，树脂还是液态，不产生残余应力。之后，随着固化反应迅速进行，由于温度场和固化度场的不均匀性而产生残余应力。在冷却阶段，残余应力迅速增大。从图9和图10还可以看出，本研究模型关于应力的预测结果与White和Kim[10]的研究结果基本一致。冷却结束时，模型计算所得的正应力为23.5MPa，比文献计算结果小6.1%，而由本模型计算所得的横应力为31.4MPa，比文献计算结果小5.4%。

图9 复合材料层合板间点(5.08，0，1.27)处正应力σ3的变化情况Fig.9 Development of interlaminar normal stress σ3 at the point (5.08, 0, 1.27) of the composite laminate under manufacture recommended cure cycle

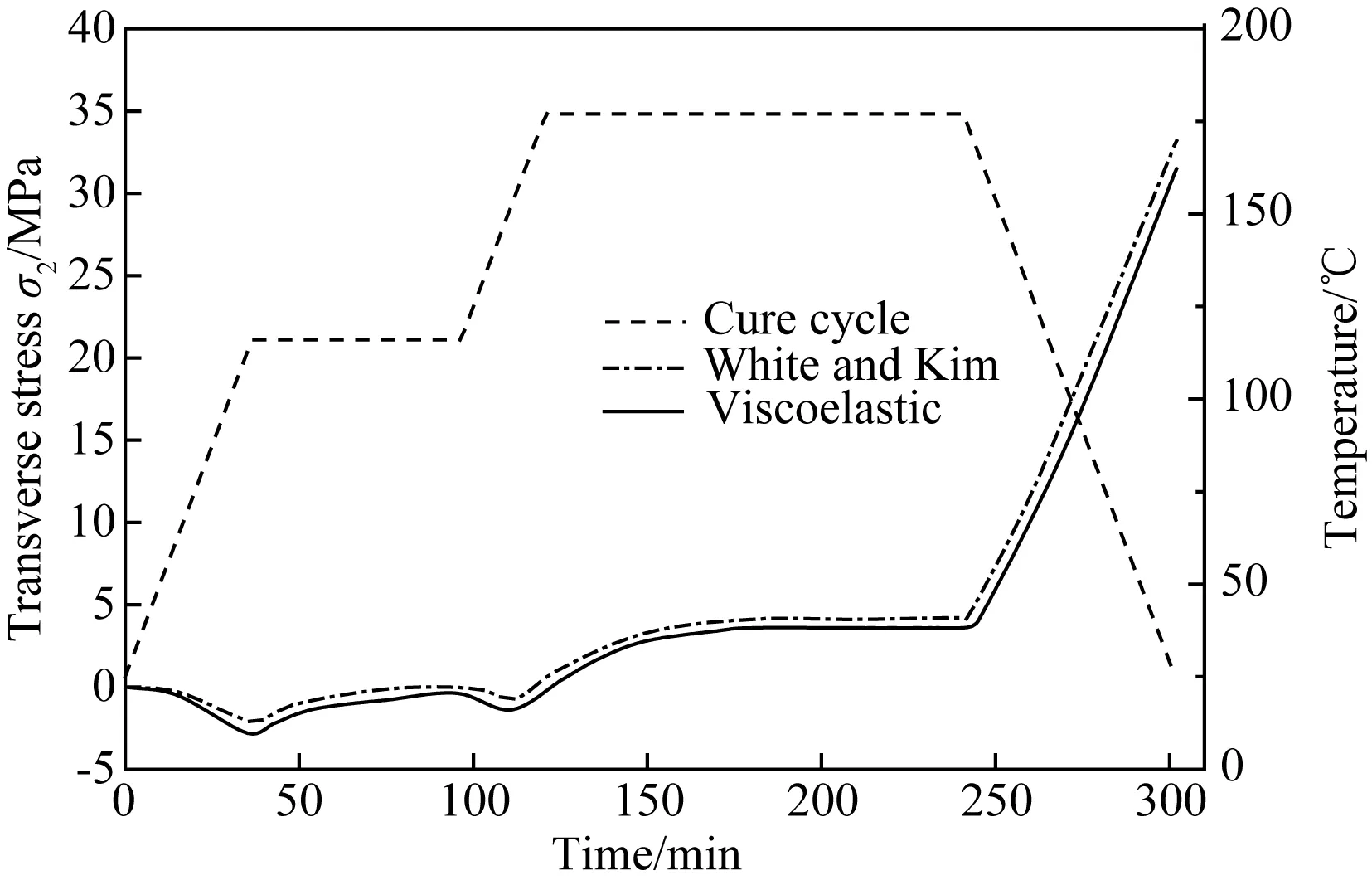
图10 复合材料层合板在0°层中点(5.08，5.08，2.22)处垂直于纤维的横应力σ2的变化情况Fig.10 Development of transverse stress σ2 being perpendicular to the fiber in the 0° ply at point (5.08，5.08，2.22) of the composite laminate under manufacture recommended cure cycle

图11为冷却结束时，层合板的Von Minses 应力切面分布图。如图所示，由于层合板内温度梯度较大，内部应力相比周围区域相差较大。

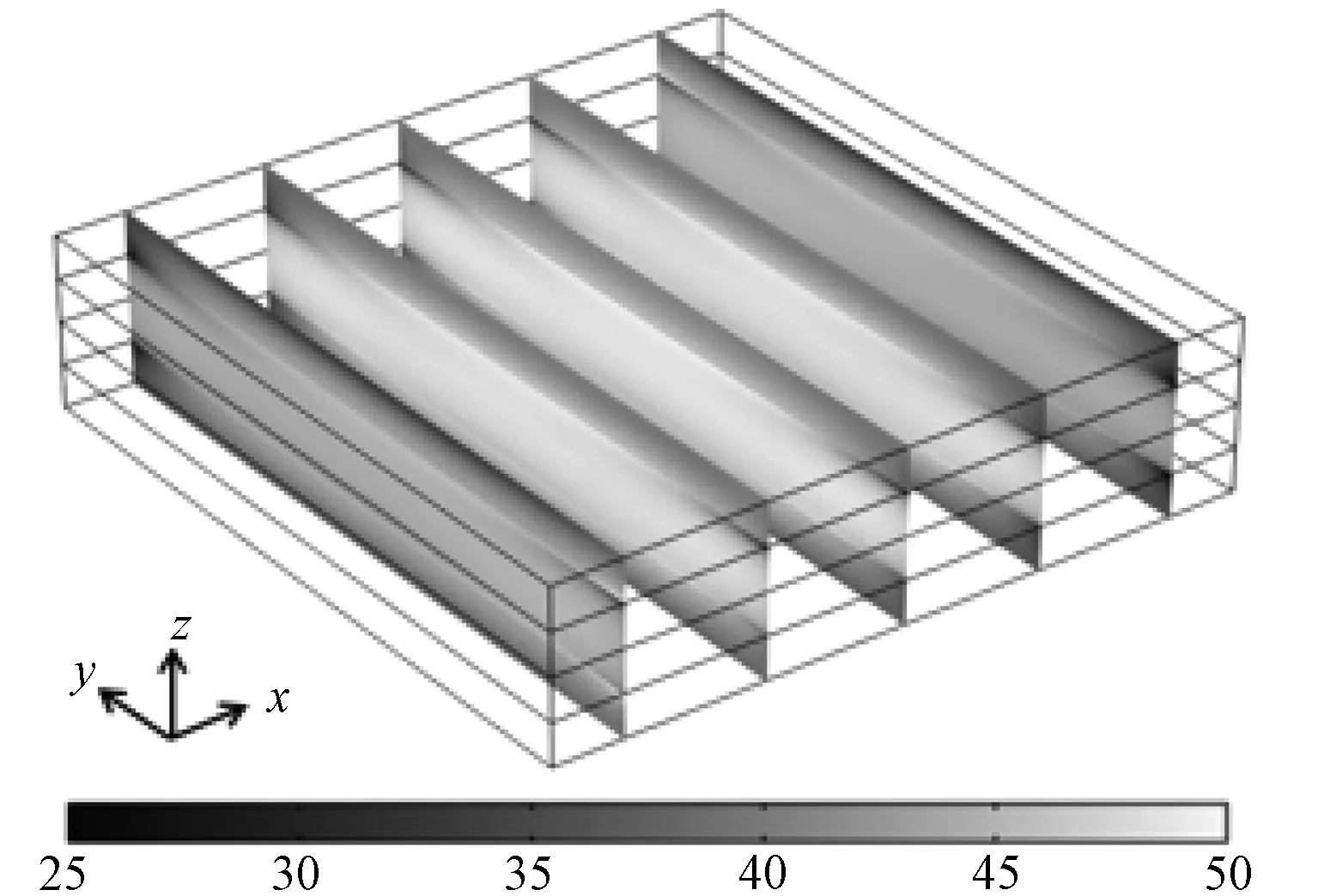
图11 复合材料层合板在固化结束时Von Minses 应力切面分布图Fig.11 Sectional drawing of Von Minses stresses at the end of cure cycle from the two models

本研究建立了热固性树脂基复合材料层合板固化过程三维有限元分析模型，并考虑了材料性能参数的时变特性，实现了热化学模型和粘弹性力学模型的多物理场耦合计算。

预测了AS4/3501-6复合材料层合板固化过程中温度场、固化度场及残余应力场的分布情况，与White 和 Kim所做研究相比，计算结果基本一致，但固化过程中层合板中心温度峰值减小2.3%～2.5%，固化反应开始时间提前约10min，最终固化程度下降0.01，冷却结束后的正应力减少1.4MPa，横应力减少1.7MPa。

本研究的研究方法具有较强的适用性，对优化固化工艺参数，提高固化质量具有一定的指导意义。