基于BP人工神经网络的动力电池SOC估算方法

苏振浩，李晓杰，秦 晋，杜文杰，韩 宁

（1中北大学能源动力工程学院，山西 太原 030051；2中北大学机械工程学院，山西 太原 030051）

为应对能源危机、减少温室气体排放，新能源汽车成为未来汽车工业发展的趋势[1]。相比燃油汽车，新能源汽车的续航里程无法得到有效解决。在目前技术条件下，电芯的制造技术相对成熟，大量电芯组成的电池组受电芯不一致影响明显，进而影响到汽车的续航里程。

动力电池荷电状态（SOC）预测成为电池管理系统（BMS）的关键技术[2]。准确地估算SOC能够提高电池的安全性能，有效保护电池，延长电池的充放电循环寿命，提高电池的使用效率[3]。因此，SOC的估算在动力电池管理系统中尤其重要[4]。SOC不能直接测量[5]，传统的以端电压为测量对象无法得到精确的SOC值。目前市场上电池SOC估算模型主要有等效电路模型和电化学模型[6]。其中，比较典型的方法有开路电压法、安时积分法、数学模型法、卡尔曼滤波法[7-10]、扩展卡尔曼滤波法[11]和神经网络法等[12-14]。开路电压法精确度不够，也不适合电池状态的实时估计[15]。安时积分法造成的误差自身无法消除，卡尔曼滤波法基于电压电流数据的采集，估算出剩余电量的最小方差，实现初值和误差的修正，但此方法只适用于线性系统，用于非线性的电池系统建模得到的SOC估算精度必将大幅降低。电化学模型需考虑电池内部的电化学反应，建立过程复杂、模型体积庞大、计算难度高、无法实现实际应用[16]。本研究将以三元锂电池为实验对象，使用电池充放电设备采集动力电池的充放电电流、电压和温度等数据，并在上位机实时读取电池SOC值。通过建立等效电路模型进行数据修正，消除电池老化产生的极化内阻对数据采集的影响。以BP人工神经网络为研究手段，建立神经网络模型，实现动力电池组SOC的估算，探讨所建立的BP人工神经网络模型对SOC估算的准确度。

1 等效电路模型建立

1.1 电池老化分析

一个完整电池包由大量单体电芯组成，通过串并联为电动汽车提供足够的能量及动力性能。在电池工作过程中，电池包内电芯单体无规律的老化问题成为电池状态估算的难点。随着工作时间的增长，电池的性能会变差，容量损失和功率损失增大。极化内阻（包括欧姆极化、浓度极化和电化学极化）也会随着循环次数的增加而增大，成为影响电池数据采集精度的主要因素[17]，而建立等效模型可以有效避免极化内阻对数据采集的影响。

1.2 模型建立

电池的内部反应是一个复杂的非线性过程，而Thevinin模型能够很好地表示此过程，本文选择建立Thevinin等效模型对电池工作原理及现象进行分析。等效后的模型由电压源、内阻及一阶RC串联组成，如图1所示。此模型无复杂参数，且可以较好地表示动力电池的动态特性。

R1表示电池的欧姆内阻，包括电解液、隔膜及正负极板等，也可表示电池充放电过程中的电压突变现象。一阶RC表示电池使用中的极化电容和电阻，Uc为其两端的电压。Rp和Cp表示电压的变化特性。在模型的建立过程中，充分考虑电池内部的极化现象，降低极化反应对电池数据采集的影响，该模型充放电过程的数学公式表示为

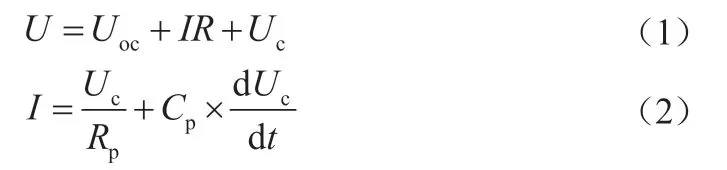
整理得修正后端电压的计算公式为

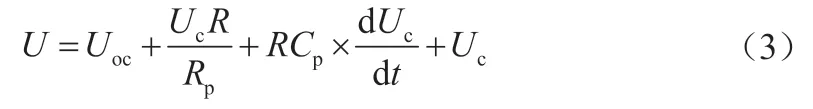
1.3 数据修正

文献[18]中提出了一种模拟电池单体放电过程中的温度场变化方法，但该方法主要针对小倍率放电有较好效果。在文献[19]中，考虑到电池使用过程中电池内部化学反应的敏感性及状态的难以估计，不同的放电倍率及不同的温度对电池极化的影响，根据Peukert方程得出电池容量与放电倍率的关系

通过n值和k值便可得出不同放电倍率下电池的容量修正值C(I)=It=KI1-n。

通过电池容量与温度关系实验得到不同温度条件下电池容量的修正值：C(I,T)=KηTI1-n。受电池内部化学反应的影响，充放电倍率、温度等都对电池数据的采集精度造成一定的影响，对采集到的数据进行修正，修正后用于网络模型的训练，将大幅度提高模型的估算精度。

图1 等效电路模型Fig.1 Equivalent circuit model

2 神经网络简介

2.1 神经网络的结构

人工神经网络通过一定的结构将功能简单的神经元组织起来，实现数据群体的并行处理。根据连接方式的差异，神经网络可分为分层神经网络和相互连接型神经网络。根据动力电池数据采集及SOC估算特点，采取多层前向型神经网络，其结构如图2所示。

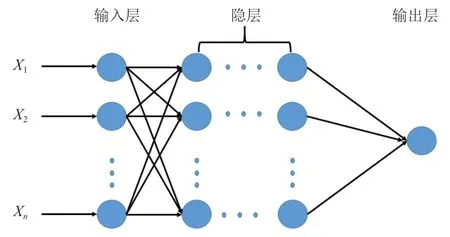
图2 神经网络结构Fig.2 Neural network structure

多层前向型神经网络的结构一般分为3层：输入层、隐含层和输出层。外部的信号由输入层接入，各输入单元将输入信号传送给隐含层的各单元。隐含层作为神经网络结构内部的处理单元，根据不同的网络需求其层数也不同。输出信号则经输出层输出。

电压、电流、温度及内阻作为电池重要参数，决定着电池组的SOC估算精度。而内阻的精确采集较为困难，以前3项参数为参考因素，以4.2 V三元锂电池为实验对象，通过数据采集训练进行网络仿真。

2.2 神经网络的学习

神经网络的学习基于对大量数据的训练，也是网络模型调整自身参数的过程。其可以通过对自身参数的调节，提高自身的学习能力，达到对环境的了解。

学习方式有两种，有导师学习和无导师学习，学习算法一般有以下两种。

（1）Hebb学习算法

同时兴奋的两个神经元会加强彼此之间的突触连接，即连接权值增大，其数学表达式为：

式中，ΔWij为两个神经元之间连接权值的变化量；Vi和Vj为神经元i和j的输出；η为学习速率。

（2）δ学习算法

设网络的输入、输出样本数据对为（Xk，Dk），网络实际输出为Yk，其中

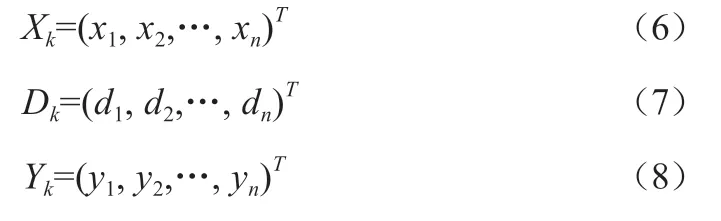
则可用下列式子表示δ学习规则：

式中，ΔWij为两个神经元连接权值Wij的变化量；Vi为神经元i的输出；η为学习速率；δj为以下函数对神经元输入参数的偏导数

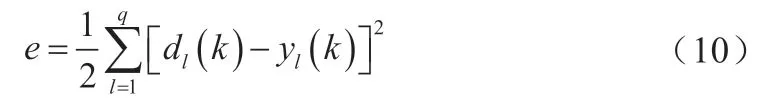
3 数据的准备

以三元锂电池为实验对象，具体参数为：标称电压为3.8 V，单体额定容量为74 A∙h，充电上限电压为4.25 V，下限电压为2.75 V，最大放电电流为2 C（以148 A电流放电）。由于单体电芯在制造、使用及静置过程中不可避免会产生单体不一致性，这种差异也会直接带给成组之后的电池模组及整个电池包。在实际使用过程中，随着电池包工作循环次数的增加，BMS内部的均衡模块会对各单体间的差异进行均衡，最大限度消除不一致性。而本次实验中，为尽可能降低单体不一致性对实验数据采集的影响，选用最新成组并通过质量测试的电池包，此时的单体不一致性最小，对实验数据采集影响、采集误差也最小。

以恒翼能高精度电池测试系统HYN-HTEI-750V300A-Z为测试平台，以48串三元锂电池组作为实验对象，先对电池组静置处理30 min，后对电池组进行完全充电处理，待电池组充满电后，静置30 min后开始数据采集。以148 A电流开始恒流放电，采集放电过程中的总电流、总电压及各单体电压及单体温度。待完全放电后，静置30 min，随后进行充电测试，采集数据，上位机显示SOC达到60%时，结束充电，静置30 min，实验结束。电池测试平台每1 s采集一次数据，整个实验过程收集到大量数据，整个实验过程中，采集到的数据量达到了35万个以上，处理掉无用数据，数据采集工作结束。

4 神经网络建模

函数拟合是网络模型建立的重要内容，通过建立模型，导入训练数据，进行网络训练，实现非线性函数的拟合，最终完成网络预测功能。本次实验以准备好的4512组，每组63个数据作为样本，4303组数据作为训练样本，用于网络训练及测试网络的拟合性能，209组数据作为测试样本，网络训练结束后，用于预测函数输出，最后对预测结果进行分析。具体的算法流程如图3所示。

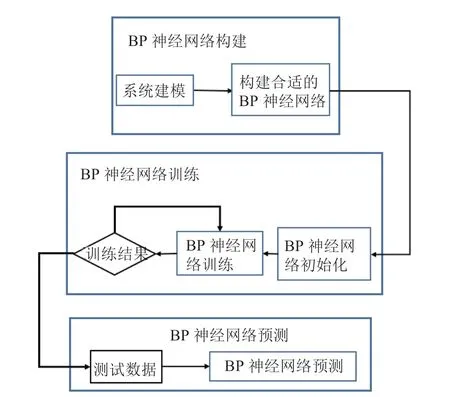
图3 算法流程Fig.3 Algorithm flow

4.1 函数拟合

神经网络模型建立后，将单体电池电压、单体温度、总电流及总电压等数据导入模型，进行训练。总的数据导入为63组，故输入层节点数为63。SOC作为模型训练的唯一目标，所以输出层的节点为1。隐含层的节点数由式(11)确定

式中，h为隐含层节点数；m为输入层节点数；n为输出层节点数；a为1～10之间的调节常数。

在MATLAB中打开人工神经网络窗口，导入准备好的数据，设置训练样本80%，验证样本10%，测试样本10%。训练函数为trainlm（Levenberg-Marquardt BP训练函数），性能函数为mse（均方误差函数），学习函数为learngd（基于梯度下降法的学习函数），传递函数为tansig（S型的正切函数），迭代次数初始设置为100次。

建立好的神经网络模型如图4所示。

图4 网络模型Fig.4 Network model

设置的隐含层个数为9层，根据训练结果进行隐含层个数的修改。

4.2 网络训练

网络参数设置完毕，将建立好的模型进行数据训练。训练结果如下文所述。

由回归图（图5）可以看出神经网络的训练、验证和测试的结果。对于一个好的拟合，其数据应该沿45°角线，表示输出等于期望。本次拟合输出结果的R值均大于0.99，表明拟合在理论方面是较优的，也表明所建立的神经网络模型是较优的。由性能图（图6）可以看到，本次函数拟合最佳迭代次数为86次。

图7为训练模型自动生成的部分误差数据值，前图为网络输出的估算值，后图为输入值与估算值的误差数据。由图8可以看出，误差稳定在0.2～0.3之间，最大误差为0.8，网络输出值与网络训练目标值基本一致，说明建立的网络模型是成功的。此网络可以用于实验数据的预测。

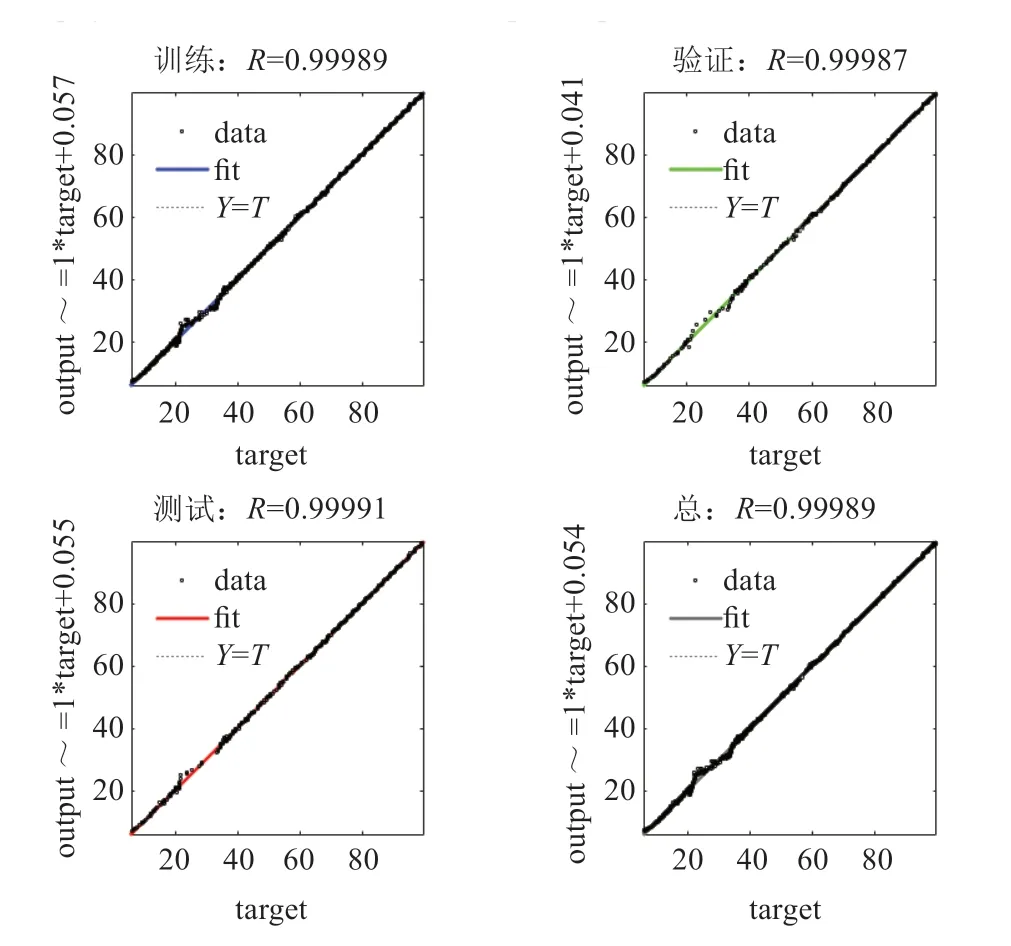
图5 回归图Fig.5 Regression graph

电池数据的采集和SOC的预测是复杂的非线性系统，神经网络对此类系统预测的精确度高低依赖于数据量基础，数据的缺乏将大大降低预测的精度。本次试验收集到整个电池包完整的充放电循环数据用于函数拟合，海量的数据提高了函数拟合的精确度，增强了训练网络的稳定性。

综上所述，拟合函数较优，网络模型性能稳定，接下来将建立的网络模型用于实验数据的仿真，进行SOC的估算。

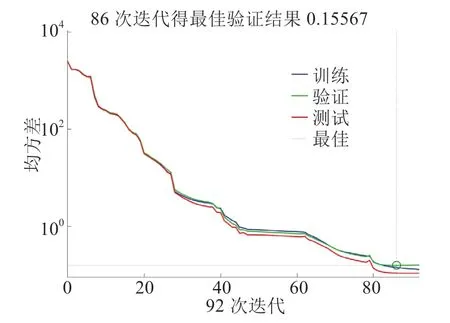
图6 性能图Fig.6 Performance diagram

图7 网络训练输出结果与误差数据Fig.7 Output and error data of network training

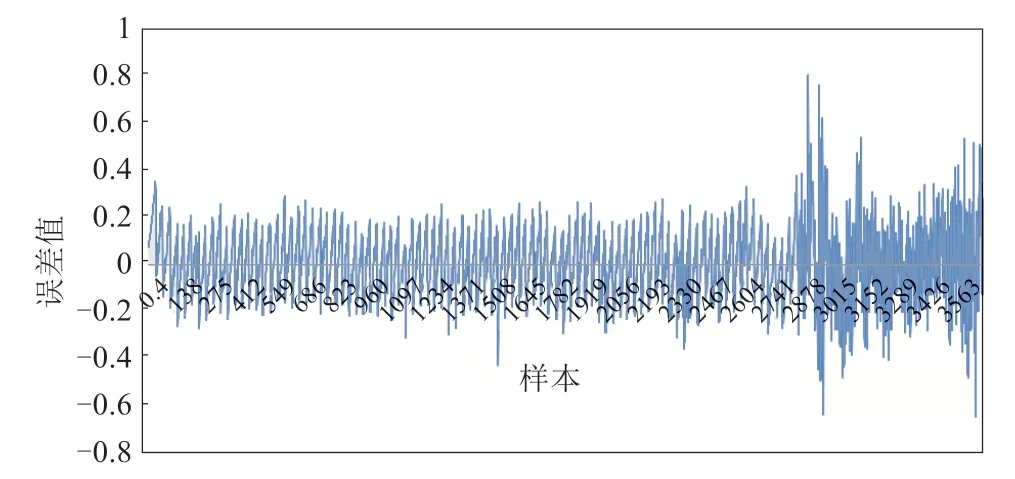
图8 误差图Fig.8 Error graph

5 实验仿真

训练好的神经网络模型，将直接应用于实验数据的仿真。仿真结果如图9、图10所示。

图9中，蓝色曲线为实际数值曲线，红色曲线为预测数值曲线。由仿真结果可以看出，在所测试的209组数据中，SOC的预测数值曲线基本沿SOC实际数值曲线变化。在实际的测试数据中，SOC数值是实时变化的，每秒的SOC都会产生轻微变化，但受采集精度影响，实际的SOC曲线并不是平滑的，而表现为阶梯状。在预测结果中，数据变化更平稳，曲线图也更平滑，函数预测效果较优。训练好的模型用于数据预测，见图10，预测误差结果位于±0.8之间，由于放电末期电池的温度及内阻抗增大的影响，SOC的误差值波动范围较大。

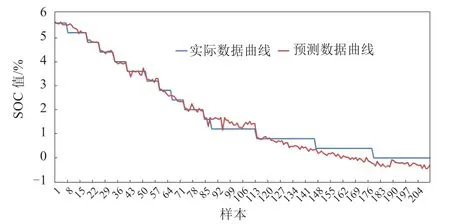
图9 SOC仿真曲线Fig.9 SOC simulation curve

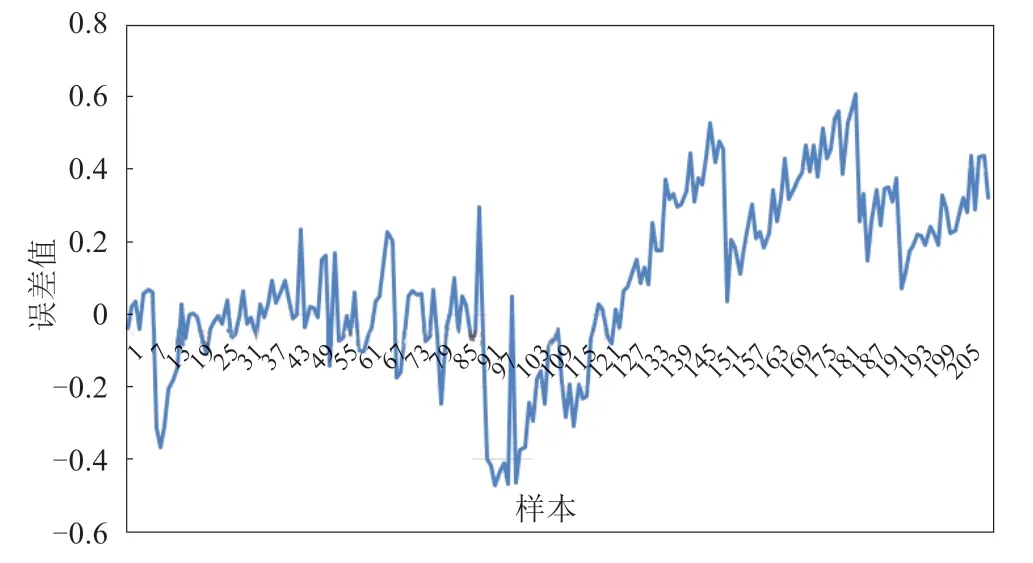
图10 SOC误差曲线Fig.10 SOC error curve

6 结 论

动力电池SOC的估算一直以来都是行业内的研究热点。依据电池高精度测试系统采集数据，通过建立等效电路模型及神经网络模型实现对电池剩余电量的估算，结果表明：

（1）采用整包电池组实验采集到庞大的数据量，数据量直接影响函数的拟合性能，数据基础的提高可以有效提高估算结果的有效性；

（2）通过分析电池老化及建立等效电路模型，建立修正公式对采集到的数据进行修正，可以有效提高数据采集的准确性；

（3）提高精度的同时结合神经网络处理庞大数据量的可靠性能实现函数拟合，应用于SOC的估算，相比于当下研究较热的白箱模型和灰色模型估算剩余电量，神经网络在模型复杂程度低、可高效处理大量数据的前提下保证了估算结果的准确性及可靠性。