基于图像处理的纱线捻系数与明度关系研究

金佳冰 郭明瑞 傅佳佳 卢雨正

(江南大学，江苏无锡，214122)

1 研究背景

捻系数作为纱线的一个重要参数，影响着纱线各方面的性能，学者们对于纱线捻系数的研究着重于对纱线质量的影响，如力学性能中的断裂强度、断裂伸长率、断裂功等[1]。此外，捻系数还影响纱线的外观形态，如毛羽、条干不匀、纱疵等，其中捻系数对纱线光泽的影响不可忽略，但这方面的研究相对较少。在环锭纺的成纱结构方面，由于纱线捻回角的变化，纱线表面的螺旋纤维角度发生改变，表面反射特征也由此发生变化，即纱线颜色的RGB值会随之改变，这导致了纱线光泽上的差异；从色彩理论方面来说，在视觉效果上主要是明度的差异。目前一些企业存在同种色纤维不同纺纱方式所纺制的同一号数纱线颜色存在差异性、生产样品与用户需求样品有色差等问题，这些色差可能会导致用户退货，给企业造成损失。因此在满足纱线性能及用纱条件的情况下，找出环锭纺纱线表面明度的变化规律，尝试微调捻系数，以达到调整纱线明暗效果的目的。

由于Datacolor测色仪孔径的限制，直径较小的纱线无法满足其测色要求，一般通过后道织造工序，或是将纱线绕于黑板上来保证样品的不透光性[2-4]，间接地对织物进行测色，但是这两种方法在经过后道工序后，纱线的卷绕方式或织物的组织结构对纱线的颜色有很大影响，不能直接体现出纱线的表观颜色。另一种方法是利用DigEye对绕于白色纸板上的纱线进行测色，其采用数码相机进行拍摄，但是与显微镜相比，其放大倍率与清晰度的限制导致无法从细节上反映出纱线的表面形态。

近些年学者们对于单根纱线表面反射特征进行了研究，同时建立了光照模型，这些模型可作参考，但各自都存在弊端。王志东等把单股未加捻纱线当作圆柱模型进行模拟[5]，但模拟的纱线表面亮度渐变速度过快，边界暗处范围过大，效果不理想。张瑞林等把纱线当作椭圆柱模型进行模拟[6]，此模型纱线表面光度渐变自然，但是这两种模型都把纱线模型理想化，不能反映出纱线捻度的特征。喻飞等对数码纱的外观进行了仿真，增加了捻度的模型[7]，但此类方法主要体现为数码纱的混色效果，其光照模型较为生硬，不能很好地体现出捻度对纱线表面细节的影响。

为此，我们利用超景深显微镜对不同捻系数的纱线进行拍摄，通过图像处理法提取图片中的像素点，并进行数据分析，探究纱线表面最真实的图像信息及其规律，为后续更加准确地建立纱线的光照模型、分析纱线的颜色提供思路。

2 图像采集

采用VHX-5000型超景深三维数码显微镜(基恩士公司)对280、320、360、400、440五种捻系数的原液着色蓝色纤维环锭纺纱线进行图像采集，拍摄前需为电动XY平台设定原点，调整电动XY平台的高度，将变焦环的倍率进行相应的调整，焦距设置为35 mm，进行图片的实时深度合成，并将纱线不同的三处位置进行拼接，分辨率设置为5 166 pixel×1 215 pixel，标尺为500 μm。以280捻系数为例，如图1所示。

图1 280捻系数环锭纺纱线超景深显微镜图像

3 图像处理

3.1 图像处理流程

采用超景深显微镜拍摄的原始图像需用Matlab R2014b对其进行相关的处理，处理流程如图2所示。

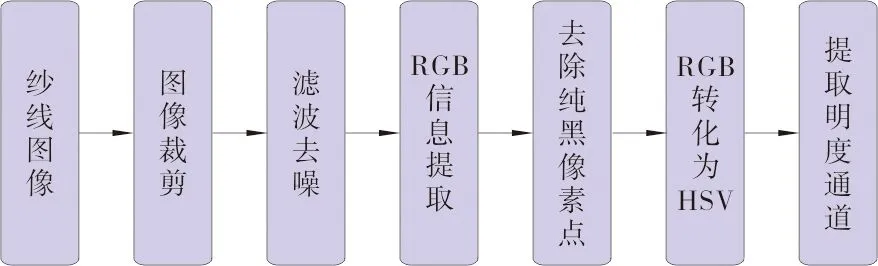
图2 图像处理流程图

3.2 图像裁剪

为突出纱线表面捻度细节，运用imcrop函数，按照同一起点、同一长宽度的条件，将5种捻系数纱线图片均裁剪为500 pixel×100 pixel的规格，以280捻系数为例，如图3所示。

图3 裁剪后的500 pixel×100 pixel的图像

3.3 中值滤波去噪

中值滤波是一种非线性滤波[8]，它是一种保护边缘的非线性图像平滑方法，在图像增强中应用广泛。中值滤波的平滑效果优于均质滤波，在抑制噪声的同时还能够保持图像的边缘清晰，在Matlab软件中，运用medfilt2函数进行图像的中值滤波去噪，每个输出像素为m×n领域的中值，如3×3、5×5、7×7、9×9等模版。由于中值滤波仅针对单通道，在不转换为灰度图像的前提下，需要对RGB三通道分别进行去噪处理。

3.4 像素点提取及颜色空间转换

在拍摄的纱线表观图像中，包含了纱线表面的所有反射光。首先读取图片，对其RGB信息进行提取，同时为了不受纯黑色像素点的影响，将其去除。由于面向硬件的RGB颜色空间不能反映明亮程度的信息，于是引入了面向用户的HSV颜色空间(HSV颜色空间中的V是指明度)，HSV空间是一种复合主观感觉的颜色模型，不同于RGB颜色空间的单位立方体，其空间结构为锥形，颜色种类H的范围为0～1，饱和度S的范围为0～1，明度V的范围也为0～1。用rgb2hsv函数将获取的纱线图像RGB颜色空间转换成HSV颜色空间，此算法建立了两种颜色空间颜色值的映射关系[9]。对采样纱线的每个点的明度通道提取明度值V，将像素点的位置设为X轴、Y轴，明度设为Z轴，绘制明度三维曲面图。

4 试验结果与分析

4.1 中值滤波去噪效果对比

由于裁剪后图片中噪点的存在，在使用图片时需对其进行去噪预处理，选用3×3、5×5、7×7、9×9模版中值滤波进行去噪，以280捻系数为例，对比图如图4所示。随着邻域范围的增大，去噪效果会加强，但是图像的清晰度也随之下降，图像细节损失严重，表面反射光的特征不能很好地体现，尤其是纱线表面纤维的凹凸效果明显减弱，因此选用3×3模版。

(a)3×3

(b)5×5

(c)7×7

(d)9×9

4.2 纱线表面明度三维曲面图

为了更加直观地观测纱线表面的反射光特征，尤其是具有捻度的环锭纺纱线表面纤维的凹凸效应，将图片中的像素点RGB信息提取后，将RGB颜色空间转换成HSV颜色空间，并提取其明度通道，以280捻系数为例，分别从原始视角，X-Y视角，X-V视角，Y-V视角作出三维曲面图，如图5所示。从图5中可以明显地看出，纱线的横向界面呈开口向下的抛物线状，表明水平方向上明度是由纱轴中心向两边递减，垂直方向上明度是由顶部至底部递减；且纱线表面并非理论圆柱或是椭圆柱模型的光滑柱体，表面凸起的纤维对光的反射率较高，呈现出明度较亮，而凹陷的纤维对光的反射率较低，呈现出明度较暗，正因为表面凸起与凹陷纤维的存在才导致了纱线的明暗效果。事实上，不光捻度，还有毛羽、条干不匀等其他因素的存在，当光照射到纱线表面时，产生一系列反射光、透射光以及被物体吸收的部分光都会影响纱线的明暗效果。

(a)原始视角

(b)X-Y视角

(c)X-V视角

(d)Y-V视角

320、360、400、440四种捻系数纱线表面的X-Y视角图如图6所示。从图6中只能观测出捻度的增大导致捻回角的增大，人眼无法直接分辨出纱线表面的明暗程度，因此需要对明度值进行正态密度曲线直方图分析。

(a)320捻系数

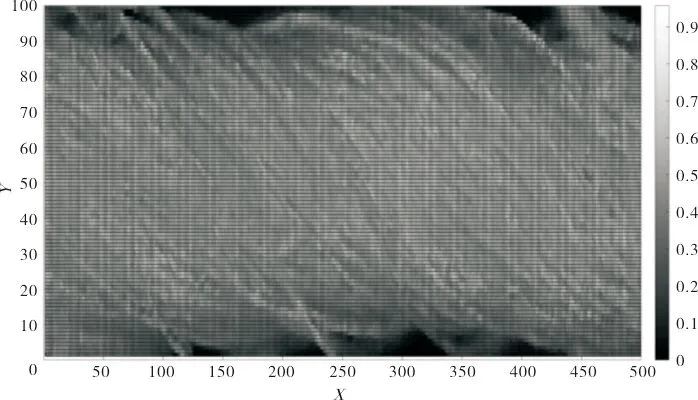
(b)360捻系数

(c)400捻系数

(d)440捻系数

4.3 纱线表面明度正态密度曲线直方图

明度值的正态密度曲线直方图如图7所示。在正态密度曲线直方图中，μ值描述的是正态分布中心的位置，当μ值变化时，其密度曲线的对称轴左右移动，μ值相当于期望值。δ值反映的是密度曲线的集中程度，相当于方差，其值越大，说明方差越大，图像越分散，反之亦然。不同捻系数纱线的μ值和δ值见表1。

图7 明度值的正态密度曲线直方图

表1不同捻系数纱线的μ、δ数值表

捻系数μδ2803203604004400.625 60.624 80.616 70.605 00.606 20.122 60.136 10.120 70.151 10.155 7

图7中纵坐标为数据点的数量，范围为0～50 000，横坐标为明度，范围为0～1，可以看出，随着捻系数的增大，正态分布中心的位置会向右发生偏移，即低捻系数纱线比高捻系数纱线整体区域明度更高。表1中的δ值在随着捻系数的增大后，整体上呈增大的趋势，说明相比于高捻系数纱线，低捻系数下的纱线表面明度分布更加集中，体现在视觉效果上为颜色更加明亮。

5 结论

(1)环锭纺纱线并不是理论上的圆柱或椭圆柱模型，其光照模型更为复杂，明度除了从纱轴中心线向两边递减外，还从纱线表面凸起纤维向凹陷纤维递减，这导致了纱线表面明亮程度的参差不齐。

(2)随着捻系数的增大，纱线表面的反射光会有所减弱，且明度分布会有所分散，在视觉效果上导致纱线颜色的变暗。与纤维混纺相比，虽然捻系数对于纱线颜色的影响较小，但在满足纱线性能及用纱条件的情况下，在调整纱线颜色方面，捻系数的微调比小比例纤维混色更易于控制，同时也为后续纱线光照模型的建立奠定了基础。