一种可用于纤维图像的聚焦评价函数
李春桥 许忠保 刘 爽 陈 威
(湖北工业大学,湖北武汉,430060)
1 研究背景
在纤维检测过程中,快速准确的聚焦是实现纤维识别的关键。显微图像自动聚焦系统多采用聚焦深度法,通过搜索聚焦评价函数曲线的峰值实现自动聚焦。聚焦评价函数主要可分为灰度梯度函数、频域函数、统计学函数和信息学函数四大类[1]。
不同类别的聚焦评价函数是根据聚焦图像与离焦图像在某一方面反映出的明显差异而建立的。灰度梯度函数是利用聚焦图像的边缘细节尖锐,在空域上表现为图像的梯度值更大的特点,通过采集图像的梯度信息作为图像清晰程度的评价依据[2];频域函数是根据聚焦图像较离焦图像具有更多的高频成分,将图像从空域转变到频域,通过计算图像的高频分量来表征聚焦图像质量的优劣[3];统计学函数是基于聚焦图像的像素灰度值具有多样性,而离焦图像灰度值被平均化这一特性,通过统计代表目标信息的像素数来区分聚焦图像和离焦图像[4];信息学函数是利用聚焦图像较离焦图像含有更多的信息熵,采用图像的信息熵作为自动聚焦的评价函数。
研究表明,频域函数计算量大,不适合快速、实时聚焦;统计学函数的聚焦精度不高;信息学函数曲线的波动较大,抗噪性低[5];而灰度梯度函数,计算过程简单,易于实现,时效性好并且聚焦效果较好[6]。
灰度梯度函数的种类多,针对具体的应用场景及灰度变化情况,函数形式可以有所变化。传统的灰度梯度评价函数有SMD函数、Roberts函数、Prewitt函数、Tenengrad函数和Laplacian函数等[7]。其中SMD函数、Roberts函数、Prewitt函数和Tenengrad函数对应一阶微分,适合目标轮廓较粗的图像,如红外图像;Laplacian函数对应二阶微分,对细节有较强的响应,适合评价边缘精细的图像[8],如生物细胞图像。而纺织纤维图像不仅具有精细的边缘,还具有明显的纵向纹理细节或鳞片结构,传统的梯度函数不能兼顾这两种信息。本文在传统梯度函数的基础上加以改进,提出了一种分数微分与整数微分相结合的纤维图像聚焦评价函数,试验该函数的单峰性、无偏性、灵敏性和抗噪性。
2 聚焦函数评价指标
理想的聚焦函数曲线应具备单峰性、无偏性、抗噪性、灵敏性和实时性等特征[9]。在聚焦评价函数满足单峰性和无偏性的条件下,本文采用陡峭度、平缓区波动量和算法耗时分别对灵敏性、抗噪性和实时性进行定量评估[10]。陡峭度S、平缓区波动量Vf计算公式如下。
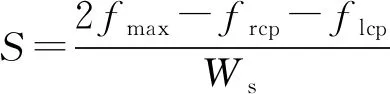
(1)
式中:Ws为陡峭区宽度,frcp、flcp、fmax分别为右临界点、左临界点和峰值点处的评价函数值。S越大,说明聚焦平面附近的函数值变化越剧烈,即灵敏性越好。
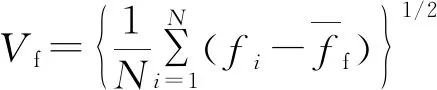
(2)
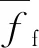
本文中,算法耗时t取每组10次试验的平均值,理想的聚焦函数应当满足耗时t越小越好。
3 新聚焦评价函数
3.1 理论基础
灰度梯度评价函数的实质是检测图像的边缘(高频信息),由于边缘像素的灰度变化短促,可以采用一阶微分和二阶微分来反映这种局部变化。本文的研究对象为纺织纤维,清晰的纺织纤维图像具有锐利的边缘和大量明细的纹理(中频信息),而整数阶微分较适合于检测图像高频变化的边缘,对自然图像中具有非连续边界点且有中频变化特性的纹理部分无能为力[11]。
分数微分运算可以大幅提升图像边缘和纹理细节信息,同时非线性成分有所保留,且提取的边缘信息能避免产生较大的噪声[12]。分数微分经过较长时间的发展,渐渐被引入数字图像处理并成功解决许多图像增强、图像去噪等问题[13]。
为了更有效地评价纤维图像的质量,本文在检测高频信息的同时,加强对中频信息的检测,综合图像的高频和中频信息作为图像清晰程度的评价结果。
目前的分数微分算子主要是0阶~1阶和1阶~2阶,其中0阶~1阶的分数微分算子模板为5×5甚至更大,参与计算的像素过多,计算量太大;而根据1阶~2阶微分的定义容易构造3×3模板的梯度算子且同样具有检测纹理信息的优点。但单独使用分数微分梯度函数评价纤维图像时,峰值点前后的评价值差异较小,得到的函数曲线不够陡峭。为了得到整体性能较好的评价函数,本文将1阶~2阶分数微分与整数微分相结合,构造出一种新的聚焦评价函数。
3.2 1阶~2阶分数微分算子的构造
分数微分是古典整数微分的推广。根据文献[14]中得出的1阶~2阶分数微分定义,可得出二元函数f(x,y)在X方向和Y方向上1阶~2阶分数阶微分的前3项近似差分表达式如下。
(3)
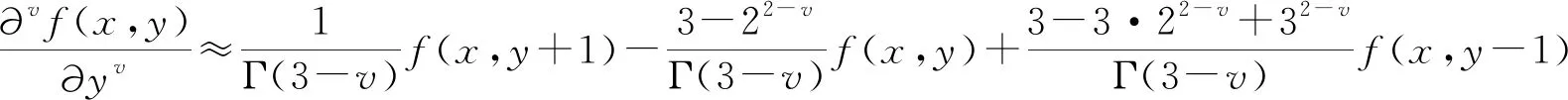
(4)
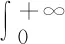
Tx+=
(5)
Tx-=
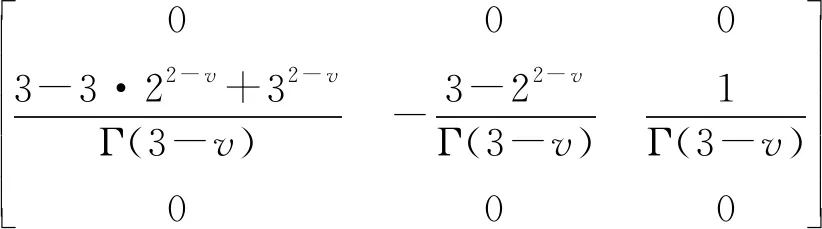
(6)
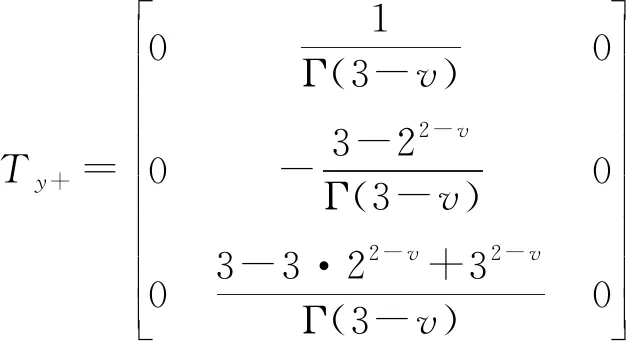
(7)
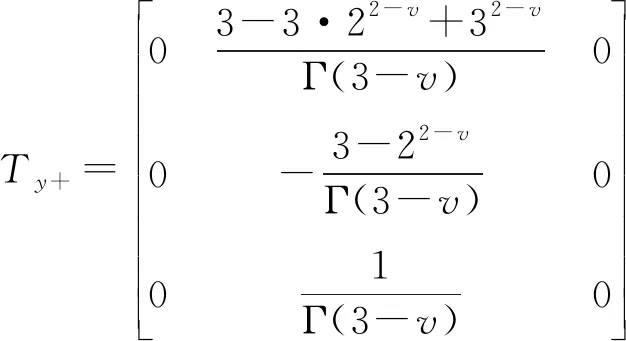
(8)
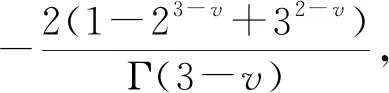
Wx=
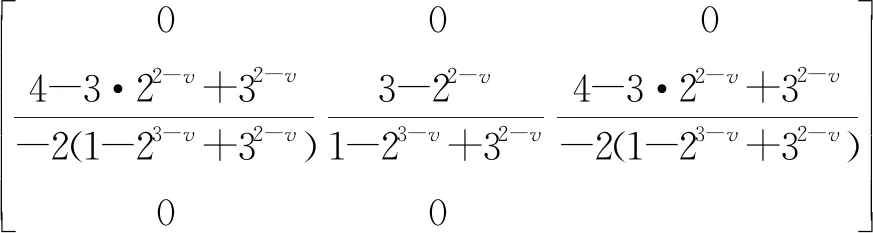
(9)
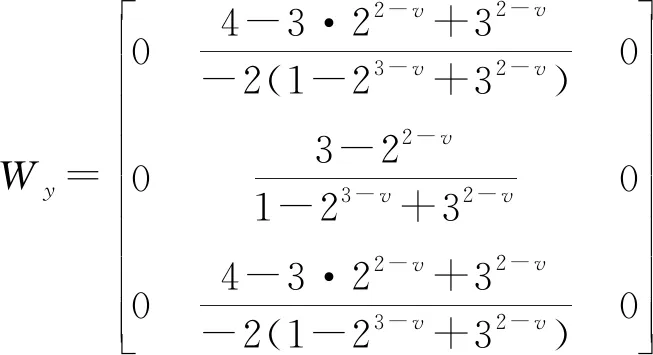
(10)
3.3 新聚焦评价函数的构造
二阶整数微分适合检测纤维的精细边缘,1阶~2阶分数微分可以较大程度地检测纹理细节。这样在利用整数微分求图像边缘部分的梯度值基础上,加上分数微分求取边缘及纹理细节部分的梯度值,共同组成聚焦评价函数。
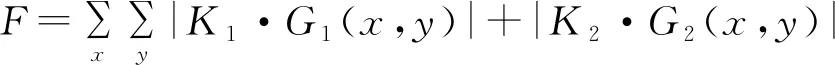
(11)
G1(x,y)=f*(x,y)⊗Tx+f*(x,y)⊗Ty
(12)
G2(x,y)=f*(x,y)⊗Wx+f*(x,y)⊗Wy
(13)
G1(x,y)>Ts,G2(x,y)>Tm
Ts,Tm为梯度阈值,G1(x,y)、G2(x,y)为图像与梯度算子的卷积结果,二阶整数微分梯度算子Tx、Ty分别为:
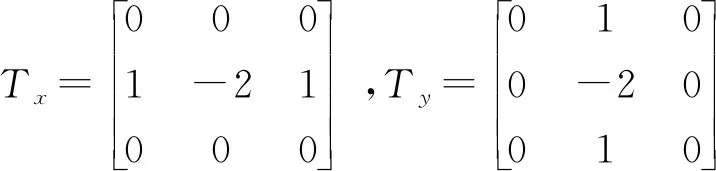
为了尽可能地减少噪声和杂质的干扰,将整数微分的梯度阈值Ts和分数微分的梯度阈值Tm分开选取。经过大量的仿真试验发现,利用整数微分求取梯度时,采用预处理后图像的标准差作为梯度阈值时效果较好;利用分数微分求梯度信息时,分数阶可变,阈值也会不同;为了简化阈值的选取,利用分数微分与图像进行卷积时统一采用预处理后图像的平均值作为梯度阈值。
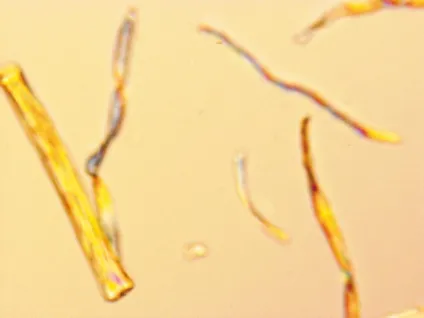
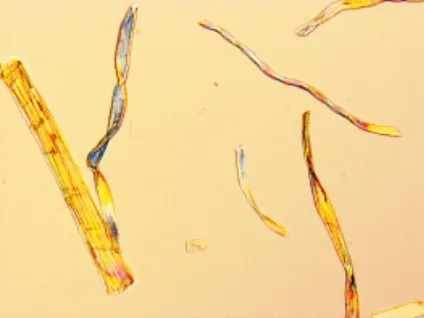
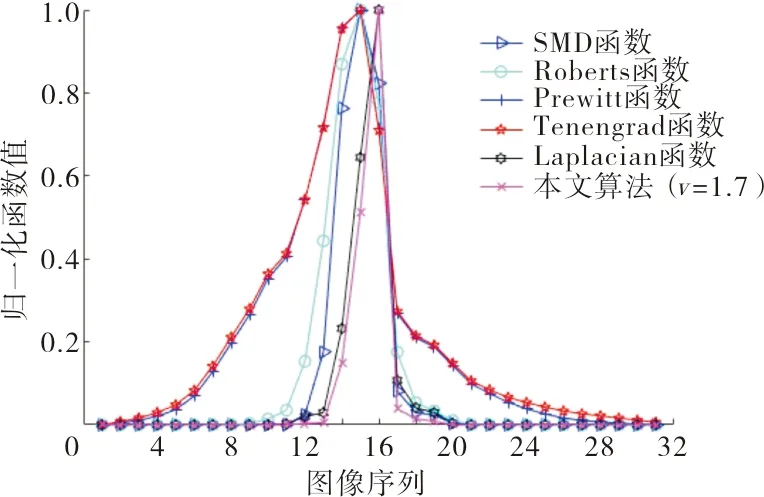
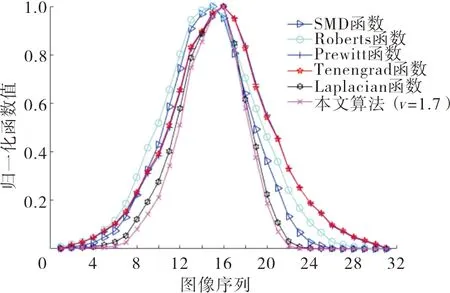
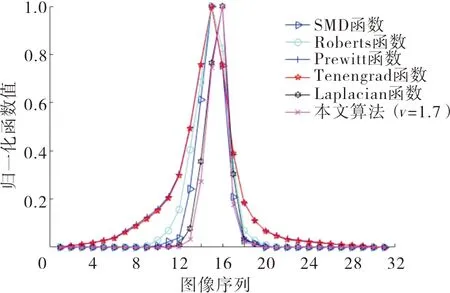
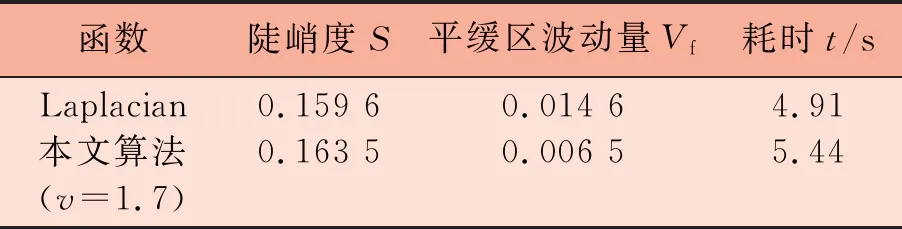
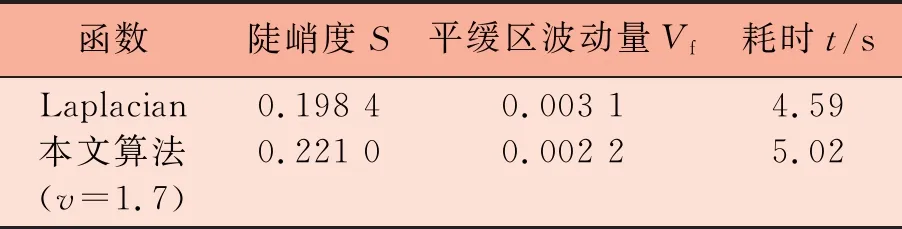
采用黄金分割法确定整数微分和分数微分各自的比例因子,相比纹理细节,图像的边缘信息更容易检测且更为重要,故取K1为0.618,K2为0.382,v为分数微分阶数(1 仿真平台:CPU为Intel Core i5-3230M,2.6 GHz,4 GB Memory;编程环境为Microsoft Visual Studio 2010。 为获取边缘凸出、纹理清晰的纤维图像,选择微分干涉相衬显微镜获取图像。目前,评价图像清晰度的方法有主观评价和客观评价两种方法。本文首先采用主观评价方法,即通过人眼观察当前帧纤维图像的边缘足够精细且纹理或鳞片结构明显时,视为准确聚焦。然后通过算法对图像作出客观评价,力图实现算法的评价结果与人眼感知效果一致。 由于不同类别的纤维具有不同的厚度,当纤维的厚度大于显微镜光学系统的景深时,同一视野中不同类别的纤维存在着不同的聚焦平面,这时可以通过选择不同的聚焦窗口实现准确聚焦。 本文共采集3组纤维图像进行仿真,分别为羊绒羊毛图像(第1组)、棉麻图像(第2组)和牦牛毛图像(第3组)。采集第1组和第2组图像时,聚焦窗口采用全屏取窗,采集第3组图像时,针对处于视野中央的单根牦牛毛纤维采用中央取窗。每组共采集31帧图像,图像分辨率1 280 pixel×960 pixel。将每组图像按照远焦-聚焦-近焦的顺序依次排列,每组第16帧纤维图像为人眼观察到的最清晰的图像。具体见图1。 (a)羊绒羊毛1帧 (c)羊绒羊毛16帧 (e)棉麻1帧 (g)棉麻16帧 (i)牦牛毛1帧 (k)牦牛毛16帧 在仿真之前,图像都需经过预处理,包括图像灰度化和中值滤波。为了减少背景、噪声对聚焦函数性能评价的干扰,SMD函数、Roberts函数、Prewitt函数、Tenengrad函数和Laplacian函数皆选用预处理后图像的标准差作为梯度阈值。图2、图3、图4分别为3组试验图像的聚焦评价仿真曲线。 图2 羊绒羊毛图像仿真曲线 图2仿真结果表明,SMD函数、Roberts函数、Prewitt函数和Tenegrad函数均在第15帧图像取到峰值,不满足无偏性要求,且灵敏性、抗噪性均不好;而Laplacian函数和本文算法在第16帧图像取到峰值,满足无偏性要求;且Laplacian函数和本文算法在平缓区几乎无波动,均表现出较好的抗噪性。且本文算法曲线的陡峭区宽度较小,灵敏性较Laplacian函数好。 图3 棉麻图像仿真曲线 图3表明,SMD函数和Roberts函数同样在第15帧图像取到峰值,不满足无偏性要求;而Tenengrad 函数、Prewitt函数、Laplacian函数和本文算法均在第16帧图像取到峰值,满足无偏性要求;并且Tenengrad 函数、Prewitt函数、Laplacian函数和本文算法曲线在平缓区皆较为平滑,针对棉麻图像均具有较好的抗噪性。但本文算法的陡峭区宽度相比Laplacian函数、Tenengrad 函数和Prewitt函数较小,本文算法的灵敏性在这些算法中仍然最好。 图4 牦牛毛图像仿真曲线 图4表明,6种算法曲线都较为平滑,但其中SMD函数、Roberts函数、Prewitt函数和Tenegrad函数均在第15帧图像取到峰值,不满足无偏性;而Laplacian函数和本文算法在第16帧图像取到峰值,聚焦准确,且仍保持较好的抗噪性和较高的灵敏性。 Laplacian函数和本文算法在3组试验中均满足无偏性要求,且在灵敏性、抗噪性和实时性方面皆表现良好,表1、表2、表3列出了Laplacian函数和本文算法的定量分析结果。 表1定量评价性能指标(羊绒羊毛图像) 函数陡峭度S平缓区波动量Vf耗时t/sLaplacian本文算法(v=1.7)0.243 90.248 50.006 80.001 74.635.26 表2定量评价性能指标(棉麻图像) 函数陡峭度S平缓区波动量Vf耗时t/sLaplacian本文算法(v=1.7)0.159 60.163 50.014 60.006 54.915.44 表3定量评价性能指标(牦牛毛图像) 函数陡峭度S平缓区波动量Vf耗时t/sLaplacian本文算法(v=1.7)0.198 40.221 00.003 10.002 24.595.02 由表1、表2和表3中的数据可以看出,在3组试验中,本文算法的陡峭度始终比Laplacian函数的陡峭度大,说明本文算法的灵敏性要优于Laplacian函数;同时,本文算法的平缓区波动量Vf值相比Laplacian函数明显较小,说明本文算法的抗噪性较好;本文算法平均每处理31帧纤维图像耗时仅比Laplacian函数多0.5 s左右,能够满足聚焦系统的实时性要求。综合分析来看,本文算法在纺织纤维图像清晰程度评价上具有一定的优势。 传统的灰度梯度评价函数只能检测高频变化的边缘信息,本文则从边缘和纹理信息两方面同时入手,将整数微分与分数微分结合使用,同时检测纤维图像的边缘和纹理信息。本文在构造的评价函数中引入了1阶~2阶分数微分,提出了分数微分与整数微分结合的聚焦评价函数,同时采用阈值处理,在理论上分析了所提算法的可行性,并与几种传统的灰度梯度评价函数进行了比较。试验结果表明:本文算法的综合性能要优于SMD函数、Roberts函数、Prewitt函数、Tenegrad函数和Laplacian函数,具有无偏性好、单峰性强和灵敏性高等特点,适合评价纹理细节丰富的纺织纤维图像。4 仿真试验与分析

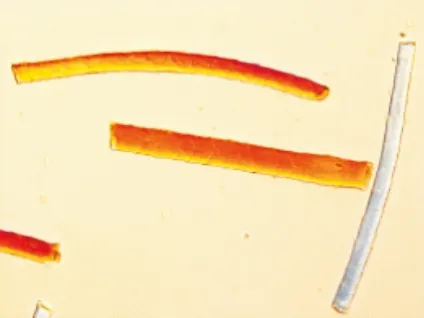



5 结论

