基于三次指数平滑法对太原市空气质量的预测

魏书禾

关键词 AQI 大气污染 指数平滑法 预测模型

中图分类号：X511                                  文献标识码：A   DOI：10.16400/j.cnki.kjdkx.2019.09.079

Keywords AQI; air pollution; exponential smoothing method; prediction model

0 引言

近年来，随着工业化的进程，社会经济的快速发展，带来的环境破坏日益凸显。各种有害气体的排放和温室效应，致使大气污染越来越严重。对空气质量课题的研究受到的普遍关注。

国内外学者对AQI问题研究。苏婷[1]利用 spss曲线估计和曲线拟合建立了三种污染物浓度值预测模型，预测安阳市的空气质量状况并提出了相关防范措施。罗运成[2]通过建立模糊综合评价矩阵，得到北京等十个城市空气污染的首要因素和AQI状况， 并提出相关改进措施。徐梦洁[3]应用秩相关系数分析和 TOPSIS分析了近几年来城市化和工业化导致空气污染指数在研究期间逐年变化的特征，对于其他南方地区环境治理具有重大意义。申胜利[4]天津市污染因素的空间分布特征进行分析，对开展大气污染防治和污染减排提供基础依据和理论参考。

此外，大气污染物具有区域扩散性， 刘世俊[5]从城市区域角度，研究某地周边城市大气污染物对空气质量的影响，分析该地区大气污染物的来源，以及为污染源的防控提出科学见解。

国外学者中，Wangdai[6]通过比较2013年各城市每日和每时的空气质量指数变化，构建关于工业化和城市化的二次曲线拟合空气质量趋势;可以看出：虽然空气质量有区域性差异，但单位 GDP能耗、城市化水平是共同因素影响AQI。

山西省地处内陆，拥有全国重要的能源重化工产业，同时不可避免的造就了大气污染最严重的城市之一。随着工业化及城镇化的发展，经济逐年提高，家庭私家车数量不断增加，以及煤矿产业持续发展，空气质量每况愈下。因此， 探讨太原空气质量评价研究是极其必要的。据统计，长期以来太原市在全国最差空气质量排行榜帮上有名，面对如此形势严峻的环境质量问题，许多学者曾进行了相关研究并提出建议。王亚辉[7]采用多元线性回归对山西省雾霾时空分布特征进行分析，找到大气气压与AQI之间的正相关的关系;闫瑞锋[8]采用分时段统计分析和GIS空间分析相结合的方法，表明太原市环境空气污染物浓度呈逐年下降趋势，环境空气质量逐步改善。目前，研究空气质量问题的主要方法有拟合曲线预测，模糊综合评价，秩相关系数分析和TOPSIS分析，ARIMA等。目的在于寻找污染的主要因素，对于整体的趋势以及空气的改善多少，并未作出判别和预测。累乘模式的三次指数平滑结合趋势因素、水平因素、季节因素，综合考虑构建平滑的模型。我们通过调整这三种因素的参数，建立累乘模式的三次指数平滑模型对太原市AQI进行分析预测。

1 模型介绍[9]

时间序列是按时间先后顺序排列形成指标的序列。时间序列分析（Time series analysis） 在各个领域中广泛的应用。时间序列的构成要素：长期趋势，季节变动，循环变动，不规则变动。时序数值由这些因素共同影响的结果。为了提升移动平均和移动加权平均算法中的大窗口、算法的简单性以及预测效果，布朗（Robert G.Brown） 提出指数平滑法Exponential Smoothing，ES）。

1.1 三次指數平滑

三次指数平滑在二次指数平滑的基础上保留了季节性的信息，使得其可以预测带有季节性的时间序列。三次指数平滑添加了一个新的参数p来表示平滑后的趋势。在自然界中有不同类型的季节性“累加性”（additive）和“累乘性”（multiplicative）运算。

1.2 三次指数平滑法的研究步骤

①收集数据，统计整理成为时间序列，并绘成时间序列统计图;②时间序列平稳性分析;③调节长期趋势、季节变动和不规则变动的参数，建立三次指数平滑模型;④Ljung-Box检验模型残差的随机性;⑤用所建立的模型预测出未来的时间序列的预测值。

2 太原市AQI拟合指数平滑模型实证分析

构建太原市AQI研究技术路线如图1：

本文所用的数据来自中国气候监测系统，2014年1月1日-2019年3月31日，维数为1936*8，数据真实有效。对原始数据中的缺失值的填补和整理统计得到，统计每月的AQI均值和每月的空气质量等级的天数，为指数平滑法建模做数据准备。2017-2018日AQI统计数据，显示空气2014-2018年空气质量等级为良最达到全年天数的45%-58%;轻度污染的全年天数占比为21%-38%;空气质量为优的天数屈指可数。详见表1和图2。太原市空气质量问题堪忧。

时间序列数据具有趋势（Trend）性和季节（Seasonality）性的特点。图2为2014-2018年每月AQI的时序图。图2中可以初步判断数据的分布具有实践性和季节特征比较明显。从图2中可以看出整个曲线处于大致不变的水平，且随机变动在整个时间序列范围内也可以认为是大致不变的，该序列可以大致被描述为一个相乘模型，因此我们可以使用三次指数平滑法进行预测。

利用R中的HoltWinters（）函数，构建采用累乘的三次指数平滑模型拟合太原市2014-2018年月均AQI。结果如图4：AQI累乘三次指数平滑进行拟合的效果：其中实线原时间序列，点线表示预测的时间序列;参数 ， ， 的取值为0.45，0，0.49。三次指数平滑模型中预测值和真实值得对比图。从中可以看出拟合值和真实值比较一致。

模型的检验主要是对残差进行检验，残差自相关和偏自相关检验。图5中：上图是残差图序列图，可见残差随机扰动明显;左下图是残差自相关图，自相关系数在第4期的时候达到了置信界限。右下图是残差偏自相关图，自相关系数在第4期的时候达到了置信界限。同时，p值远远小于0.01，说明殘差随机性检验通过。

2.5 预测

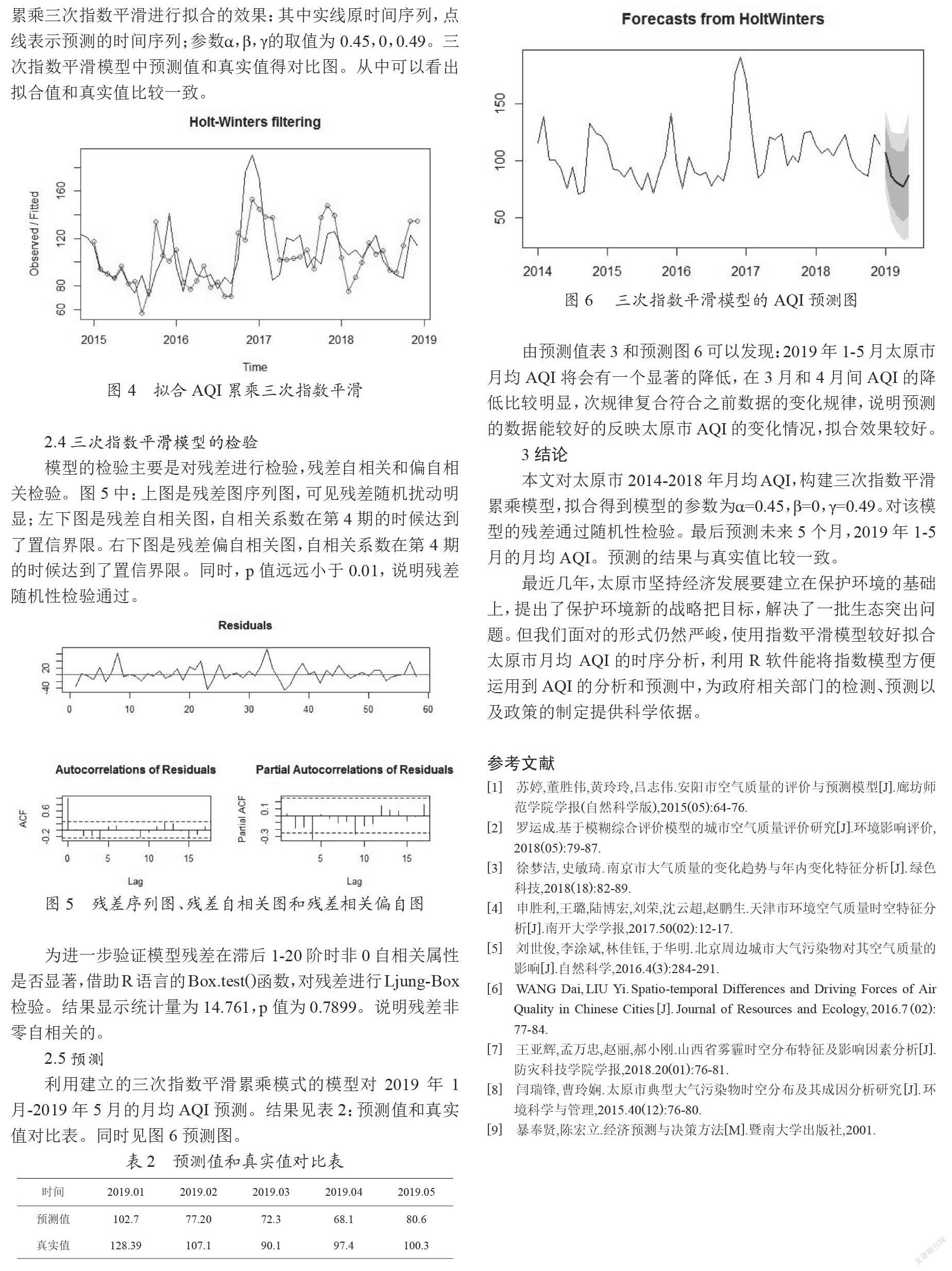
利用建立的三次指数平滑累乘模式的模型对2019年1月-2019年5月的月均AQI预测。结果见表2：预测值和真实值对比表。同时见图6预测图。

3 结论

本文对太原市2014-2018年月均AQI，构建三次指数平滑累乘模型，拟合得到模型的参数为 =0.45， =0， =0.49。对该模型的残差通过随机性检验。最后预测未来5个月，2019年1-5月的月均AQI。预测的结果与真实值比较一致。

最近几年，太原市坚持经济发展要建立在保护环境的基础上，提出了保护环境新的战略把目标，解决了一批生态突出问题。但我们面对的形式仍然严峻，使用指数平滑模型较好拟合太原市月均 AQI的时序分析，利用R软件能将指数模型方便运用到AQI的分析和预测中，为政府相关部门的检测、预测以及政策的制定提供科学依据。

参考文献

[1] 苏婷，董胜伟，黄玲玲，吕志伟.安阳市空气质量的评价与预测模型[J].廊坊师范学院学报（自然科学版），2015（05）：64-76.

[2] 罗运成.基于模糊综合评价模型的城市空气质量评价研究[J].环境影响评价，2018（05）：79-87.

[3] 徐梦洁，史敏琦.南京市大气质量的变化趋势与年内变化特征分析[J].绿色科技，2018（18）：82-89.

[4] 申胜利，王璐，陆博宏，刘荣，沈云超，赵鹏生.天津市环境空气质量时空特征分析[J].南开大学学报，2017.50（02）：12-17.

[5] 刘世俊，李涂斌，林佳钰，于华明.北京周边城市大气污染物对其空气质量的影响[J].自然科学，2016.4（3）：284-291.

[6] WANG Dai，LIU Yi.Spatio-temporal Differences and Driving Forces of Air Quality in Chinese Cities[J].Journal of Resources and Ecology，2016.7（02）：77-84.

[7] 王亚辉，孟万忠，赵丽，郝小刚.山西省雾霾时空分布特征及影响因素分析[J].防灾科技学院学报，2018.20（01）：76-81.

[8] 闫瑞锋，曹玲娴.太原市典型大气污染物时空分布及其成因分析研究[J].环境科学与管理，2015.40（12）：76-80.

[9] 暴奉贤，陈宏立.经济预测与决策方法[M].暨南大学出版社，2001.