基于HMM的高校家庭贫困生认定模型研究

谢颖 朱远胜 马维聪 张英

摘 要：为了将HMM的Baum-welch算法应用到高校家庭贫困生认定过程中，首先将学生的经济状态依据客观情况设置为5个状态，然后将得到的观测数据依据外部低成本变量进行加权处理，再将加权处理后的数据按照一定的比例划分为7个等级，对不同等级进行分段统计，并在此基础上提出了使用HMM的Baum-Welch算法解决这个问题时构建初始化参数的方法，最后将迭代的结果依据学生贫困状态期望百分比由高到低顺序进行排序，并将结果与直接计算方法及通过实际调研得到的结论进行对比，通过对比得到了HMM算法在解决此类问题中存在的局限性，同时给出了提高预测准确性的新模型建立的建议。然后将这种方法在其它班级进行了验证，以检验结论的可靠性。

关键词：贫困生认定;隐马尔可夫模型;Baum-Welch算法;期望百分比

中图分类号：G641              文献标识码：B             文章编号： 1674-2346（2019）03-0075-09

0    引言

国内在定量研究高校贫困家庭学生认定方面的成果不多，田志磊[1]通过将非收入变量，如居住地与公共服务的可得性、住房条件等作为一级指标，然后构建二级指标，再构建财富指数，然后使用主成分分析法，在构建绝对家庭财富指数时采用回歸模型。胡苗苗[2]将决策理论引入经济困难学生认定过程，将家庭经济收入、家庭人员组成、家庭健康状况，以及学生在校学习生活平均消费情况作为4个属性引入到决策分析中作为评价指标，通过决策信息矩阵进行贫困生的识别。文献[1]、文献[2]的研究都没有考虑特征信息的时序性。何源[3]使用了SQL Server数据挖掘技术挖掘贫困生消费行为和消费习惯，用学习的知识对新数据进行识别;周皞[4]将在校园卡上产生的各种消费数据按性质分类，通过建立消费总量和消费强度等特征向量，挖掘学生经济状况与消费数据的关联规则，可以为判别高校贫困生提供辅助决策依据。文献[3]、文献[4]的研究都是采用微软数据仓库的AnalysisServices工具进行联机数据挖掘，学习效果依赖于关联规则的制订。杨知玲[5]提出了从“助学贷款、家庭月收入、低保/特困户、家庭负债、勤工助学、单亲/低保”6个外部指标出发，使用决策树模型进行高校贫困生认定，忽略了学生主体作用。

国际上，美国联邦教育部建立了全国统一的家庭经济困难大学生资助申请和审核系统（简称CPS），CPS的核心是联邦学生资助需求计算公式：资助需求=入学成本-预期家庭贡献，家庭预期贡献计算复杂，要考虑家庭的年收入[1]。由于我国目前尚未建立全国范围内的收入和诚信管理系统，因此无法实施这一方法。

本文将隐马尔可夫模型（hidden Markov models 记为HMM）引入到高校家庭经济困难学生认定工作中，通过研究学生在学校的日常消费行为及HMM的Baum-Welch算法估算学生经济处于不同状况的概率期望，通过学生校内消费的外在表现，挖掘学生经济的内在状况，为判断学生的经济状况提供理论上的坚实依据和实际中可以操作的工具，这种算法能自动消除外围因素，如性别差异、地区差异，以及我国在不同经济发展时期的学生消费水平的差异等因素造成的影响，将以往通过外围因素进行的定性或简单定量分析转化为通过学生主体因素为主进行的定量分析，具有普适性、易操作性，并能够构成程序化的操作模型，从而易于在各个高校进行推广。全文数据处理流程如图1所示。

1    数据获取与数据划分

1.1    数据获取

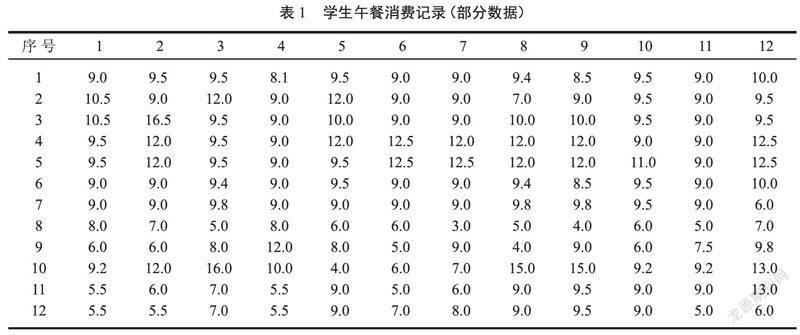
本文以€讇讇赘咝讇讇追衷簚讇讇鬃ㄒ祤讇讇装嗉段袢≌飧霭嗉兜？7位同学从2018年3月12日至4月27日连续33次午餐记录（周末和节假日除外），同时获取了其它分院的另外3个班的午餐消费记录，作为后面的算法验证数据。个别同学的午餐数据存在缺失情况，由于采取了人工统计数据，所以缺失数据量比较少，直接以这个学生的午餐消费平均值作为缺失数据的值进行填充。所获取的数据如表 1所示（每行代表1位同学，列是时间顺序）：

1.2    依据低成本变量进行数据调整

考虑学生主体消费的同时，考虑家庭因素的影响，依据文献[1]中所述低成本变量，我们分别采集父母身体状况、父母学历、父母工作性质、是否单亲家庭和是否孤儿作为外部因素，并分别对消费数据进行加权处理。所谓低成本变量是指容易获得，并且很大程度上不失真的特征信息，之所以要调整数据，因为有的同学长期低消费并不是由于经济困难造成的，而真正困难的同学日常消费也是很低的，所以，必须依据低成本变量对数据做出调整。按表 2方法将低成本变量从定性分析转换为定量计算。

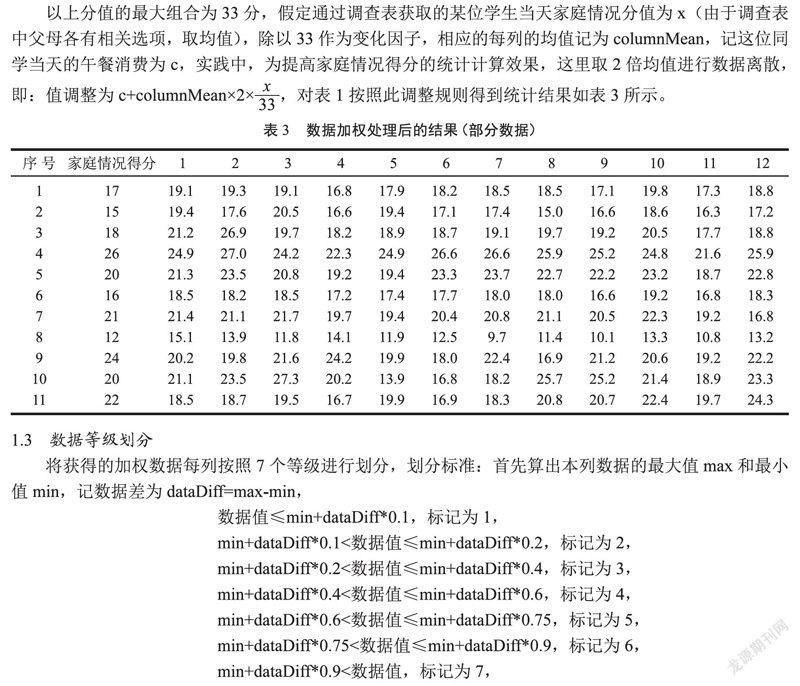
以上分值的最大组合为33分，假定通过调查表获取的某位学生当天家庭情况分值为x（由于调查表中父母各有相关选项，取均值），除以33作为变化因子，相应的每列的均值记为columnMean，记这位同学当天的午餐消费为c，实践中，为提高家庭情况得分的统计计算效果，这里取2倍均值进行数据离散，即：值调整为 c+columnMean€？€祝员？按照此调整规则得到统计结果如表 3所示。

1.3    数据等级划分

将获得的加权数据每列按照7个等级进行划分，划分标准：首先算出本列数据的最大值max和最小值min，记数据差为dataDiff=max-min，

数据值≤min+dataDiff*0.1，标记为1，

min+dataDiff*0.1<数据值≤min+dataDiff*0.2，标记为2，

min+dataDiff*0.2<数据值≤min+dataDiff*0.4，标记为3，

min+dataDiff*0.4<数据值≤min+dataDiff*0.6，标记为4，

min+dataDiff*0.6<数据值≤min+dataDiff*0.75，标记为5，

min+dataDiff*0.75<数据值≤min+dataDiff*0.9，标记为6，

min+dataDiff*0.9<数据值，标记为7，

为了使得数据较为均匀的排列，max值的获取并不都是按照最大值进行的，有时候会取第二大或第三大值作为max值，以本列中从1到7所有数字都出现为准则，比如：上述午餐消费表中的第4列最大值是37，如果以这个值为最大值，那么标识后的数据绝大多数都在1到3之间，5、6不出现，4也出现的很少，所以在这种情况下，以第二大数值26.8作为本列的最大值，当然按照这个处理规则，有的列中会多次出现7。按照上述规则，得到如表 4所示的学生午餐消费分段数据（每行代表1位同学，列是时间顺序）。

2    算法模型

2.1    模型参数

2.3    初始参数的确立

无论是EM算法还是HMM算法都是局部收敛，通常的做法是为每位同学随机设定初始参数，然后进行循环迭代，通过python的HmmLearn包，或者matlab自带的HMM统計工具箱进行测试，结果都不如人意，也就是说，仅仅依赖算法本身是没有办法获取全局最优值的，在通过学生的午餐消费记录估算学生经济状况时，采取了以下办法，尽量保证算法结果与实际情况相符合，试验证明，这种构造初始矩阵的方法是符合实际情况的。

1）状态转换矩阵A的确立

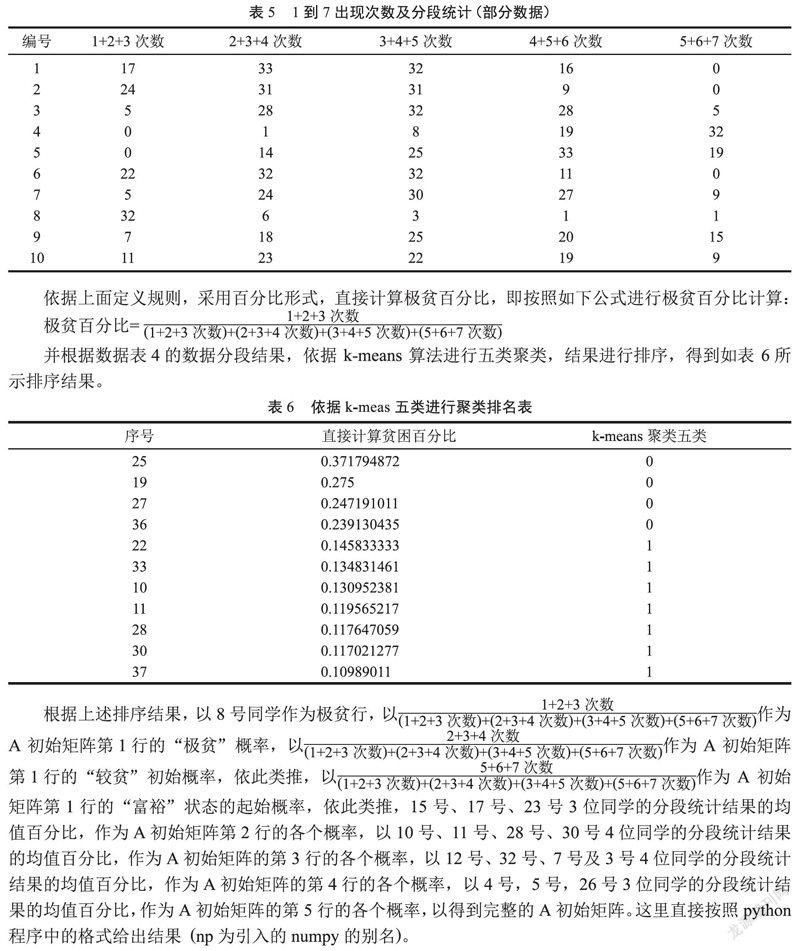
先统计每行中1到7出现的次数，然后以1出现次数+2出现次数+3出现次数的最大值作为极贫确认的依据，以2出现次数+3出现次数+4出现次数的最大值作为“比较贫困”的参考依据，依次类推，以5出现次数+6出现次数+7出现次数的最大值作为“富裕”的初步参考依据，统计结果如表 5所示。

依据上面定义规则，采用百分比形式，直接计算极贫百分比，即按照如下公式进行极贫百分比计算：

并根据数据表4的数据分段结果，依据k-means算法进行五类聚类，结果进行排序，得到如表 6所示排序结果。

根据上述排序结果，以8号同学作为极贫行，以作为A初始矩阵第1行的“极贫”概率，以作为A初始矩阵第1行的“较贫”初始概率，依此类推，以作为A初始矩阵第1行的“富裕”状态的起始概率，依此类推，15号、17号、23号3位同学的分段统计结果的均值百分比，作为A初始矩阵第2行的各个概率，以10号、11号、28号、30号4位同学的分段统计结果的均值百分比，作为A初始矩阵的第3行的各个概率，以12号、32号、7号及3号4位同学的分段统计结果的均值百分比，作为A初始矩阵的第4行的各个概率，以4号，5号，26号3位同学的分段统计结果的均值百分比，作为A初始矩阵的第5行的各个概率，以得到完整的A初始矩阵。这里直接按照python程序中的格式给出结果（np为引入的numpy的别名）。

2）发射矩阵B的确定

仍然按照上述A初始矩阵选定的各行，按照表4分别计算分段结果1到7所占的比例作为B的各行，得到B初始值如公式 2所示。

3）初始状态矩阵 确定

的确定按照倾向于贫困生的原则给出。

每位同学都以上述3个参数作为初始参数，在迭代过程中因为使用了前向和后向概率at（i）和 t（i）采用递归算法以后，前向变量和后向变量均小于1，此时会出现2个变量越来越小并迅速趋向于0的情况，预算中就有可能出现0/0情况，采取添加比例系数的办法，避免出现0/0情况发生[10]。

3    算法实现与结果的对比分析

3.1    迭代结果分析

本项目的运行环境为：win7，64位OS，inter Core i5-6500处理器，主频3.20GHz，Python3.5.3，自编软件。根据上述初始参数 、A、B，对每位同学按照最大循环次数5000及阈值1e-9进行循环迭代，并最终按照期望值百分比即：

因为要按照极贫状态由高到低进行排序，这里取i=1，得到结果如表 7所示。

按照20%资助对象进行分析，那么8号、7号、17号、19号、15号、24号、35号、5号这8位同学可以列为资助对象，但是将此数据与实际资助对象进行对比发现，8位同学中有2位同学是与实际调查结果不符合的，即：第7号同学和第5号同学。迭代算法对“极贫”8号同学的判断是准确的，也就是说，实际的准确率只有75%。

3.2    HMM迭代结果与直接计算结果对比

HMM的Baum-walch迭代结果、直接计算结果以及K-MEANS聚类结果如表8所示，其中K-MEANS聚类选择了5个类别进行了聚类。表 8是按照“贫困期望值百分比”由低到高的顺序排列的。

将直接计算得到的排名结果和实际情况进行对比，发现，除了“极贫”同学被准确命中以外，其它7位同学也被准确命中，上面所说的误判的7号和5号同学都不在前11位。

如果仅仅对比HMM算法结果和直接计算的排名结果，可以发现，按照可以对20%的学生进行资助，那么取前8名，2种结果相差2位同学，通过和班主任实际情况核实，发现：HMM的计算结果的准确性不如直接计算。也就是说，我们采取了很多办法希望保证HMM的准确性，但是与实际调查结果分析进行对比只能保证75%的准确率。而最简单的直接计算反而可以保证几乎100%的成功率。但是当资助比例降为10%～15%时，两者的交集则比较准确。这个结果到底是一种必然现象还是一种偶然现象，3.3节对另外两个班级应用上述方法进行验证。

3.3    另外班级的验证

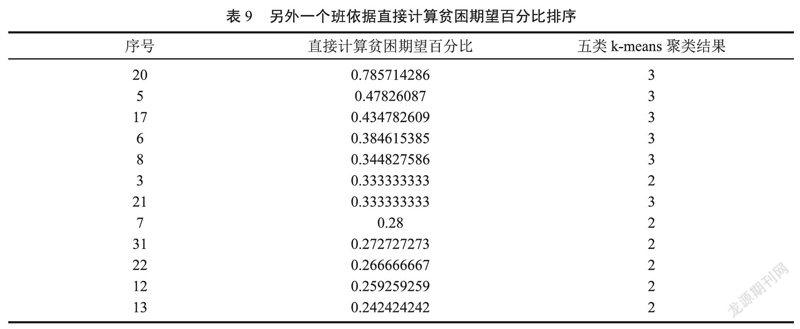
抽取另外1个班的连续11次午餐消费及家庭情况调查表，按照上面的数据加权处理、数据分段、统计、k-means聚类、构造初始矩阵、迭代，依据直接计算的排序结果如表 9所示。

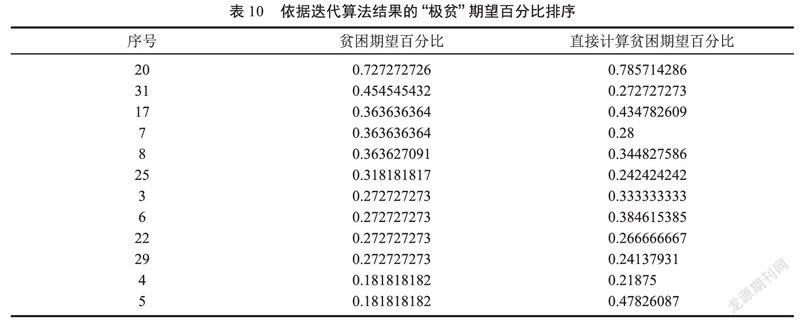
对比依据Baum-welch迭代算法得到的概率期望计算的期望百分比，如表10所示。

依据Baum-welch迭代算法得到的结果，再求其“极贫”期望百分比，得到的结果由大到小排序后，原先依直接计算得到的结果中，2条记录为新加，将2种结果提交班主任辨别，结论仍然是依据直接计算的结果更为可靠，二者都能正确地识别出“极贫”的第1位同学，在“贫困”名单中，前10名中仍然有2名差异，也就是说HMM的Baum-welch迭代算法的准确率，在这里达到了75%，而直接计算的结果反而得到班主任的认同。但是，如果资助比例降低为10%～15%，则也是两者的交集更为可信。

由于篇幅的原因，另外一个班级数据不再列出，但结论是相似的，也就是说通过上述步骤进行的HMM的Baum-welch迭代算法的准确率大概在75%左右，如果资助比例降低，则二者的交集更为可靠。

4    结论

复杂的HMM的Baum-welch算法得到的结论其准确性不如前期数据处理过程中直接使用数据分段统计结果得到的结论可靠。但二者对于“极贫”同学的判断是一致的，不过，在实际工作中，因为资助比例没有一个严格的限制，由此，我们给出高校贫困生认定的判别模型（按照10%最终资助比例）：

1）获取原始的午餐消费记录;

2）依据低成本变量并用2倍的当天消费均值对数据进行加权处理;

3）对加权处理后的数据进行分段，并进行分段统计（求和）;

4）直接依据分段求和结果进行贫困百分比计算，并进行五类的k-means聚类;

5）依据聚类结果设置HMM的Baum-welch算法的初始迭代参数;

6）根据迭代结果求直接计算和迭代结果的交集。

模型中依据外部低成本变量的2倍加权数据处理，也是在实践中通过1倍到3倍、4倍等多种加权比较后得出的结论。从实践效果来看，2倍数据加权效果最好。数据的多倍加权本质上是对外部低成本变量在算法中的权值进行调整。过高的权值会导致数据向高和低两侧集中，不利于数据等级的划分，也将导致结果出现较大偏离。

参考文献

[1]田志磊.采用非收入變量认定高校家庭经济困难学生的实证研究[J].北京大学教育评论，2010，8（2）：146-147.

[2]胡苗苗.基于多属性决策的高校家庭经济困难学生认定方法及应用[J].重庆工商大学学报（自然科学版），2016，33（2）：54-57.

[3]何源.基于数据挖掘的高校贫困生辅助辨识系统设计[J].鄂州大学学报，2015，22（10）：106-109.

[4]周皞.基于校园卡数据挖掘的高校贫困生辅助判别研究[J].职教通讯，2012（35）：59-61.

[5]杨知玲.数据挖掘在高校贫困生评价中的应用[J].软件导报，2016，15（6）：170-172.

[6]伊鹏.基于HMM的动态社会网络社团发现算法[J].计算机研究与发展，2017，54（11）：2611-2612.

[7]李昕.基于改进的隐马尔科夫模型的情感压力分级方法[J].生物医学工程学杂志，2016，33（3）：555-556.

[8]刘树伟.基于时变隐马尔可夫模型的机器人故障预测[J].机电一体化， 2016（6）：4-5.

[9]杨安驹，杨云.基于隐马尔科夫模型的融合推荐算法[J].计算机与现代化，2015（9）：61-62.

[10]张天雄.基于HMM的通信流量异常检测[J].智能计算机与应用，2018，8（4）：122-123.