基于核心素养下的小学数学开放性课堂建构

施继果

【课前思考】

数学思想是小学数学重要的核心素养之一，“建构主义”理论认为学生必须主动“投入学习”，必须在情境脉络下与问题互动才能真正理解，必须积极建构模型。通过内在对话与思考过程，与他人互动来理解脉络与解决问题。植树问题这部分内容重在向学生渗透一些解决问题的思想方法，因此，教学时借助画图的方法，运用“整体——部分——整体”之间的关系通过数形结合，让学生体会“数形结合”、“一一对应”、“化繁为简”、“变与不变”、“分类讨论”等数学思想方法，为学生的终生发展奠定基础。

【教学内容】

人教版义务教育教科书数学五年级上册数学广角——植树问题。

【教学目标】

（1）利用学生熟悉的生活素材，通过动手操作等实践活动，让学生感悟棵数与间隔数之间的关系。

（2）在具体情境中抽象出植树问题，理解植树问题，逐步建构出植树问题的模型。

（3）学生会应用植树问题的模型去解决生活中类似的实际问题。

【教学重点】

引导学生发现植树问题中棵数与间隔数之间的关系，构建植树问题的模型。

【教学难点】

理解间隔数和棵数之间的关系。

【教学过程】

一、谜语导入，聚焦问题。

猜谜语：两棵小树十个杈，不长叶子不开花。能写会算还会画，天天干活不说话。（手）

【思考：通过猜谜语引出间隔、间隔数，聚焦问题。同时让学生感知数学源于生活，生活中处处有数学。】

二、探索规律，构建模型。

（一）创设情境，呈示信息。

出示：同学们要在全长1000米的小路一边植树，每隔5米栽一棵。一共要栽多少棵树？

【思考：利用问题引领，培养学生的问题意识;创设开放的问题，激发学生参与学习的动机。】

（二）获取信息，处理信息。

你得到哪些数学信息？

⑴“全长”1000m也就是“总长”1000m。

⑵你是怎样理解“每隔5米种一棵”的？

①“每隔5米栽一棵”可以是：隔5米，栽一棵，……，隔5米，栽一棵;

②“每隔5米栽一棵”还可以是：栽一棵，隔5米，……，隔5米，栽一棵;

③“每隔5米栽一棵”也可以是：隔5米，栽一棵，……，栽一棵，隔5米。

⑶如何理解“一边”？

【思考：培养学生获取、处理信息以及利用信息分析问题的能力。培养学生严谨的数学思维，学会深层次、多角度地思考，激发学生开放的研究策略。尽可能给学生多一点思考的时间、表现自己的机会、尝试成功的愉快，让学生知识与能力得到同步发展，心理素质得到全面提高，使他们的思维达到一定的广度和深度。】

（三）鼓励猜测，大胆质疑。

想一想，一共要栽多少棵树？怎样列式？

列式：1000÷5=200，这里200到底表示什么呢？（明确200是间隔数。）

引导得出：总长 ÷ 间隔距离=间隔数，

那200个间隔要栽几棵树？我们一起来画图验证一下？分组完成。

【思考：让学生知其然，也知其所以然，充分感知数学中的“理”。】

（四）化繁为简，建立模型。

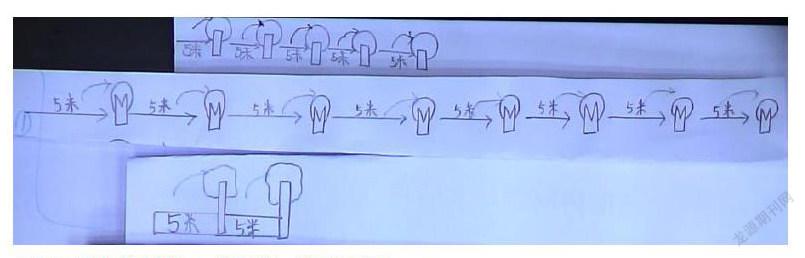
（1）让学生在作业纸上画图验证;

学生自主画出部分图形后，遇到了麻烦：因为间隔数太多，画起来太麻烦了。

【思考：直观感知和动手操作是促进学生思维发展的一种有效手段。让学生体验繁杂的数学问题，为后面寻找简单的解决策略做好铺垫，也为学生操作创造开放的时间与空间。同时借助画图的方法进行研究，可以把植树问题这种比较抽象、易错的问题简单化、直观化。】

（2）选择学生画出来的局部“部分”进行研究，并且把研究成果进行引导分析，建立模型;

200个间隔数太多，画起来太“繁”，那我们不画可以吗？现在我们就一起来研究一下。

①只栽一端：棵数=间隔数

②两端都栽：棵数=间隔数+1

ƒ两端都不栽：棵数=间隔数-1

數学中像这样的问题称为植树问题（板书：植树问题）。接下来，我们就运用植树问题的规律去解决1000米小路上的植树问题。

【思考：通过数一数“一个间隔一棵树”或“一棵树一个间隔”这样的“数”与“形”之间的对应关系，体会“一一对应”思想，从而理解间隔数和棵树之间的关系，并运用不完全归纳法建立数学模型。借助“整体——部分——整体”之间的关系进行“化繁为简”，把研究“整体”转化成研究“部分”发现规律，从而解决“整体”的问题，引导学生在发现规律的过程中感悟“化繁为简”的思想方法。同时体会数学中“变与不变”的数学思想，“变”的是我们研究的方法、策略、学习的材料，我们选取的是“整体中的一小部分”、是简单的、便于观察和操作的作为研究的对象，从而得出规律建立模型。“不变”的是数学的本质、数学的模型，我们由“部分”得出的规律对“整体”同样适用。】

（五）应用规律，解决问题。

同学们要在全长1000米的小路一边植树，每隔5米栽一棵。一共要栽多少棵树？

你们现在能回答“一共要栽多少棵树”吗？（分三种情况，此时学生会分类思考）

【思考：让学生运用数学模型解决问题，更进一步体会“化繁为简”的数学思想，同时渗透分类讨论的数学思想，让学生养成良好的数学思维，严谨的思考习惯。】

四、走进生活，感悟数学。

（一）感悟生活中的植树问题;

安装的路灯、隔离桩、项链上的水晶……

（二）拓展知识，课堂延伸。

引入“皮克定理”，引导学生终生学习。

【思考：让学生感受到数学源于生活，而又服务于生活，体会到数学的价值以及本身的魅力。】