水文站流量测验代表垂线分析原理及应用
刘炜 王怀柏 段雯 胡跃斌 李兰涛
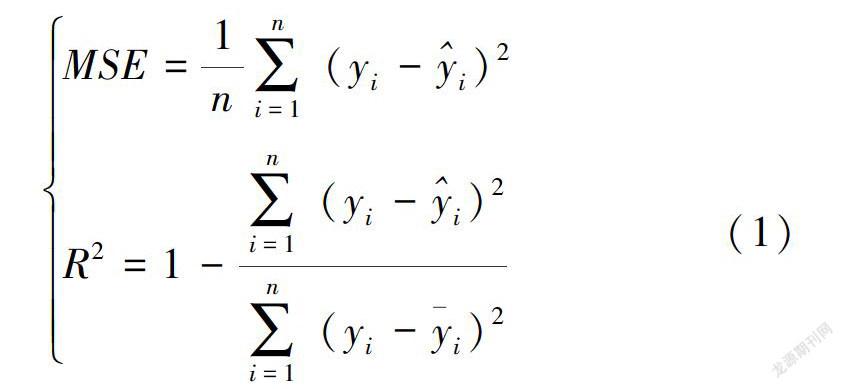
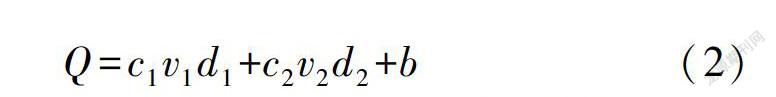

摘要:以龙门水文站基上155断面为例,选取该断面1974-2012年约640个实测断面流量测次作为分析数据集,起点距每隔2m选取一条垂线,对垂线水深和断面平均水深进行线性回归,并计算决定系数和均方误差,用决定系数作为评价指标,优选出最佳代表垂线位置。结果表明:若在龙门站基上155断面起点距分别为54、188 m处设置固定垂线实测流速和水深,使用回归公式来计算流量,则可以达到标准差229 m3/s、相对标准差5%的估算精度。
关键词:线性回归;代表垂线;流量测验;龙门水文站
中图分类号:TV856;TV882.1
文献标志码:A
doi:10.3969/j .issn.1000- 1379.2019.04.002
水文站在常规流量测验中,常通过施测均匀布设在测流断面上各条垂线的水深和流速来计算流量。通过代表垂线分析,可以建立少量垂线实测要素与全断面测量结果的回归关系,在实际测验中只在这些垂线位置进行要素采样,从而达到降低工作强度、提高测验效率的目的。此外,若选取的代表垂线[1]能避开流速较大的中泓范围,则可在一定程度上降低高洪测验作业的危险性。
1 代表垂线分析的基本原理
代表垂线分析[2]的目标是寻找少量垂線,使得在这些垂线处某个水文要素的实测值可以代表该要素的全断面综合值。代表垂线分析包括回归分析和垂线优选两部分。回归分析[3-4]是指对给定的垂线位置,以目标要素的垂线观测值为自变量、全断面综合值为因变量建立回归关系:垂线优选是指对不同垂线的回归结果进行评价比较,选出符合一定精度指标的代表垂线位置。
流量测验所涉及的目标要素包括水深、流速、流量等3项。根据对问题性质的推断,本文采用线性回归算法(一元或多元)[5]建立模型,通过穷举法优选垂线位置。回归模型的构成见表1。
回归结果评价采用均方误差(MSE)和决定系数(R2)两个指标。它们的计算公式分别为式中:n为样本数量;Yi为实测值;Yi为预测值;Yi为实测值均值。
2 实例分析结果
2.1 水深代表单垂线
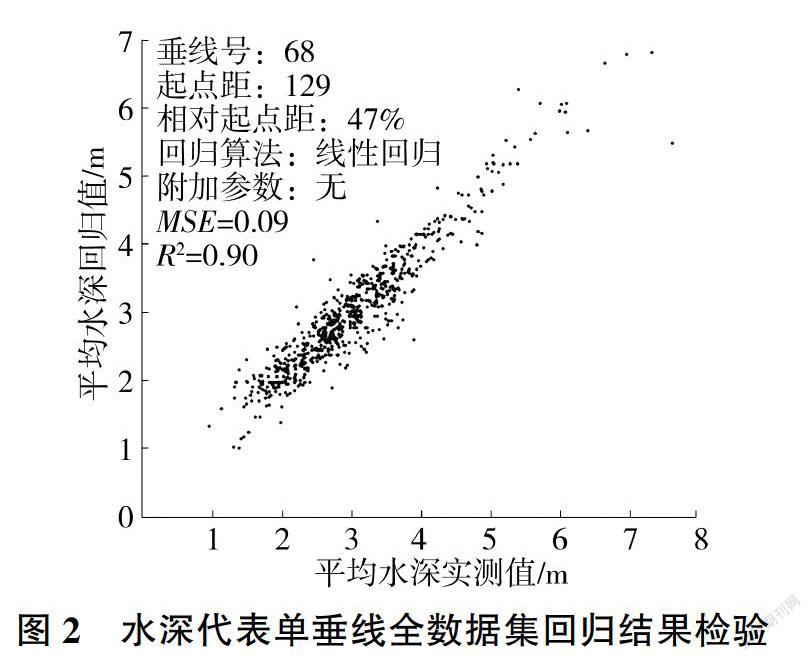
水深代表单垂线法是指使用一条垂线的实测水深来回归计算断面平均水深。以龙门水文站基上155断面为例,具体步骤为:选取该断面1974-2012年约640个实测断面流量测次作为分析数据集,起点距每隔2m选取一条垂线,对垂线水深和断面平均水深进行线性回归,并计算R2和MSE。用R2作为评价指标,优选出最佳起点距垂线位置。
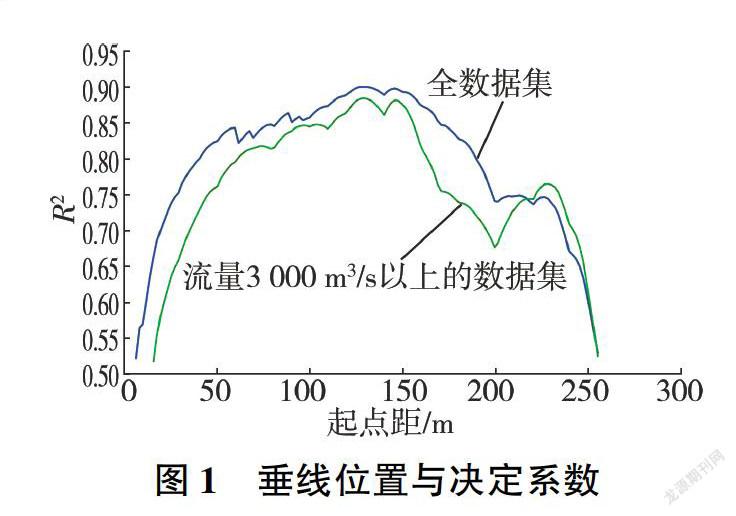
不同流量级的最优代表垂线位置不同,代表性也有差异。本文按全数据集和流量3 000 m/s以上的数据集分别进行计算。垂线起点距及相应的R2见图1。最优水深代表垂线大致在断面中间位置,若以决定系数大于0.85为标准,则代表垂线的可选起点距区间为(113,155)。全数据集最优代表垂线的回归结果检验见图2。
2.2 水深代表双垂线
水深代表双垂线是指使用两条垂线实测水深来回归计算断面平均水深。其优选方法与单垂线类似,也是寻找具有最优代表性的垂线位置。两者区别在于,双垂线是在由两个垂线起点距构成的二维空间里进行计算和优选。
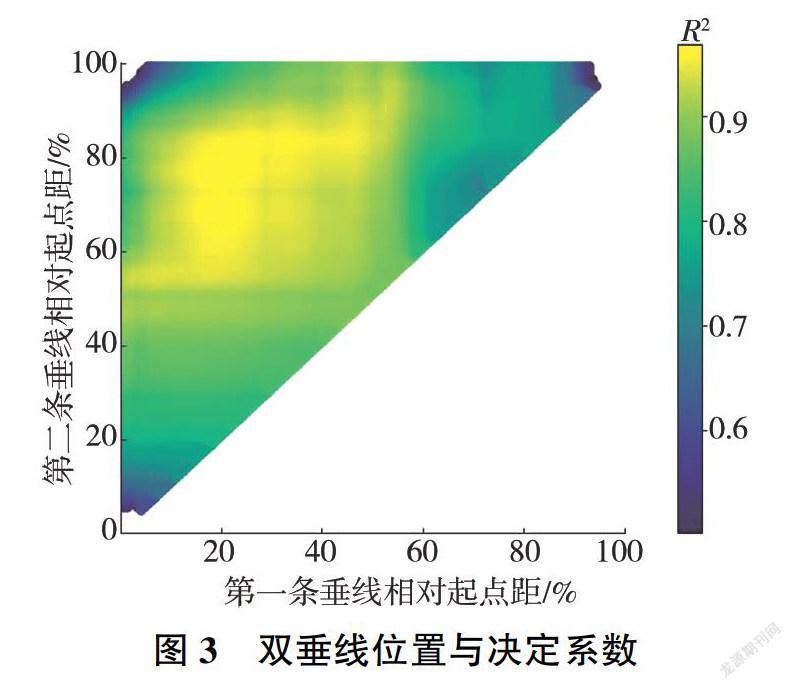
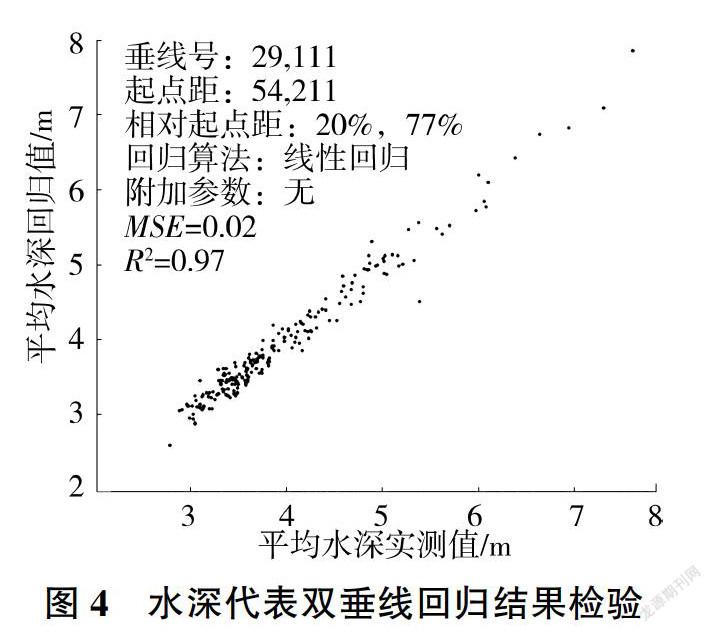
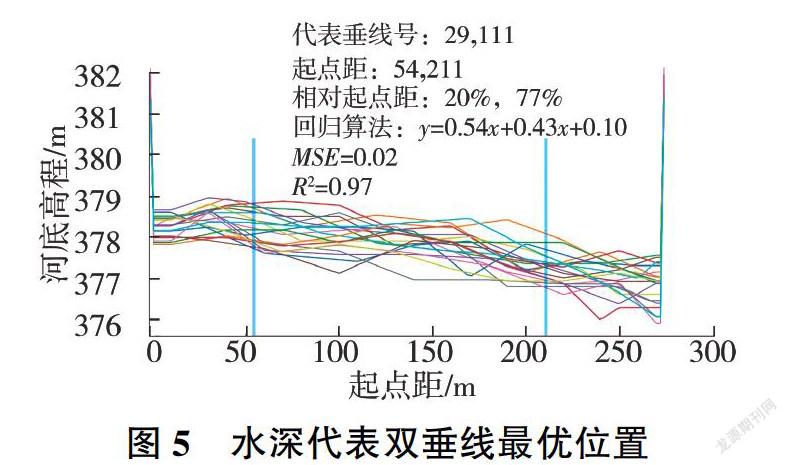
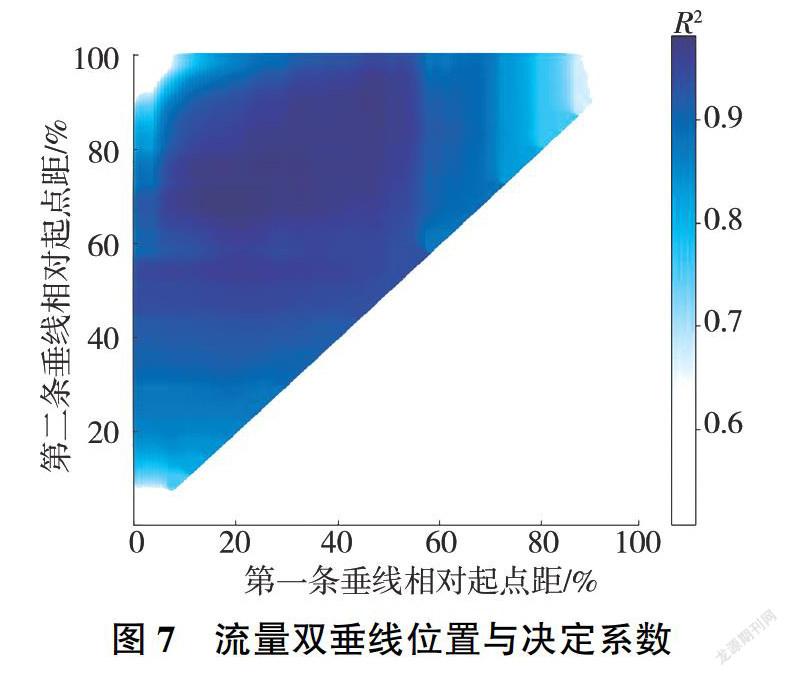
在具体算法中,采用穷举策略对所有有效垂线位置组合(按2m起点距步长,共10 129对组合)进行回归分析和指标计算,R2分析结果见图3,图中横.纵坐标分别为第一、第二条垂线的相对起点距(相对于全断面宽的百分比)。由图3可知,R2的最大值出现在空间偏左上位置,对应的两条垂线(相对起点距分别为20%、77%)即为最优水深代表双垂线,其回归结果检验及位置示意见图4、图5(图5中不同颜色的线条表示不同测次的河底形态)。
2.3 流速代表双垂线
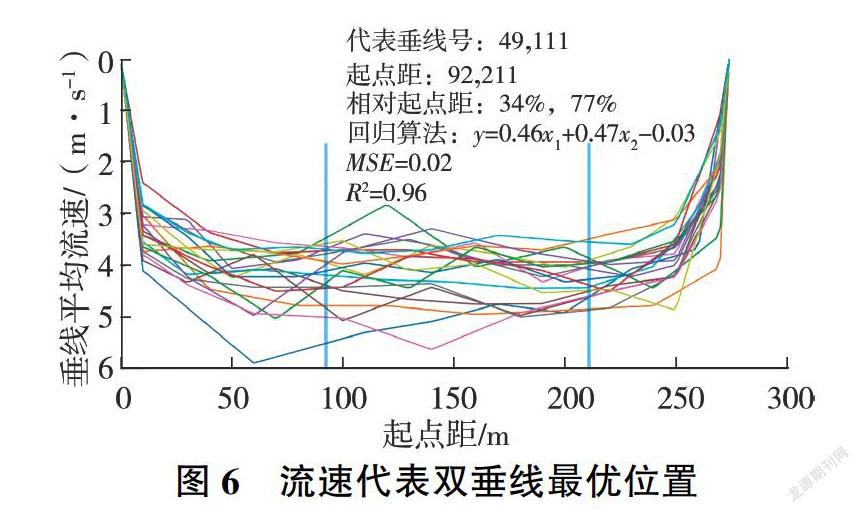
采用类似的方法也可以得到流速代表垂线。用一条或两条垂线的实测流速代人回归方程,得到断面平均流速。经分析,最优流速代表双垂线的R2为0.96,MSE为0.02,其位置见图6。
2.4 流量代表双垂线
流量代表双垂线是指用两个起点距位置的水深和垂线流速来回归断面流量。流量代表垂线法更符合生产实际需要,依据流量的构成原理,设计回归公式形式为
Q=C1vld1+C2V2d2+b
(2)式中:Q为计算流量;v1、d1分别为第一条垂线的流速和水深;v2、d2分别为第二条垂线的流速和水深;c1、C2为回归系数。
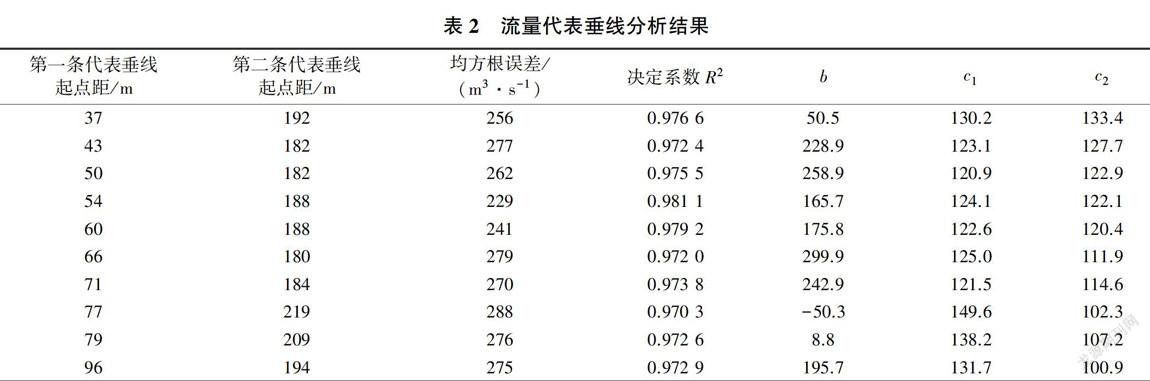
龙门水文站基上155断面的R2分析结果分别见图7、图8。图7为全空间的遍历搜索结果,图8为将R2大于0.95的区域放大并重新渲染的结果。图8表明,存在一定的垂线选择范围,在此范围内的代表双垂线均具有足够的代表性。随机抽取R2大于0.97的10对起点距位置(包含最优解),回归分析结果见表2。
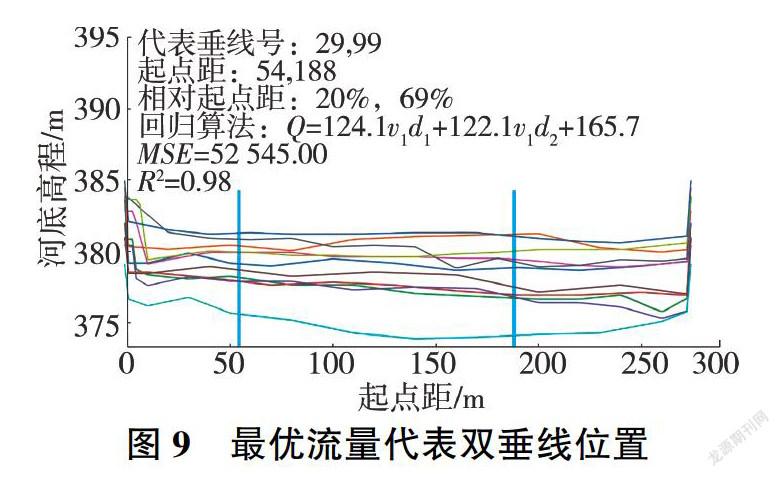
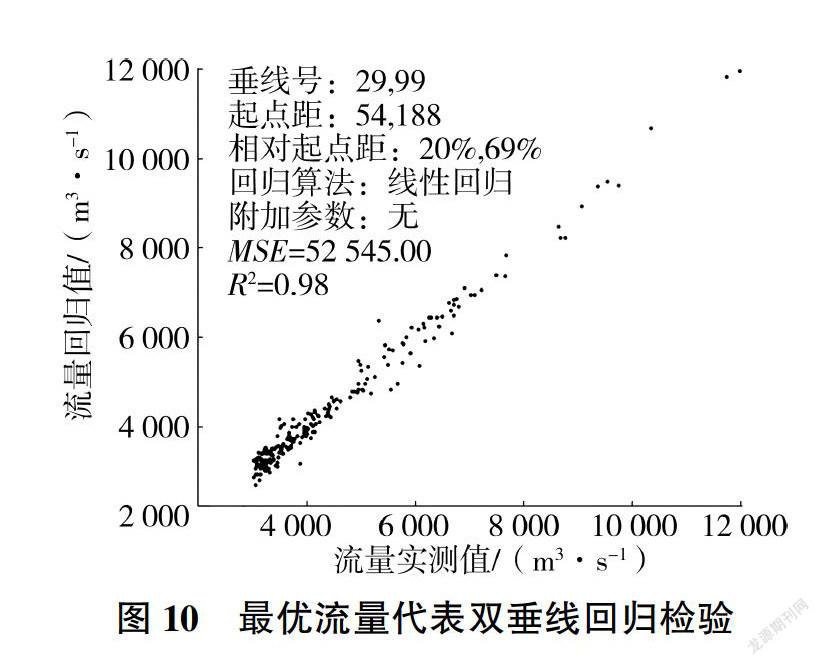
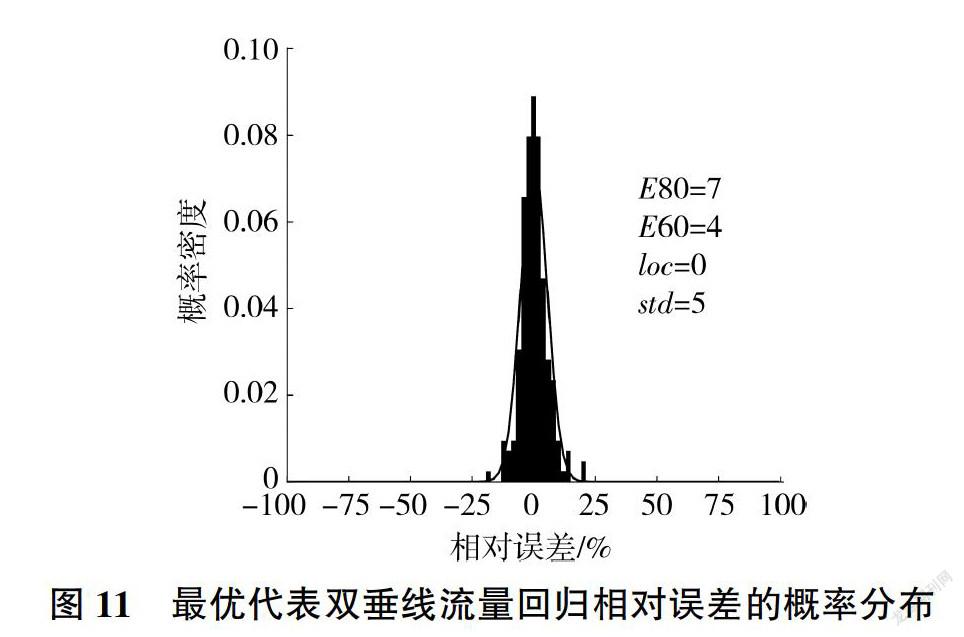
最优垂线位置(相对起点距20%和69%)见图9,相应回归检验结果及流量相对误差的概率分布见图10、图11(E80、E60、loc、std分别为保证率80%对应的误差、保证率600-/0对应的误差、误差均值、相对标准差)。
表2、图9-图11说明,若在龙门基上155断面起点距分别为54、188 m处设置固定垂线实测流速和水深,使用式(3)来计算流量,则可以达到均方根误差229 m/s、相对标准差5%的估算精度:
Q= 124.1 vld1+122.1 V2d2+165.7
(3)
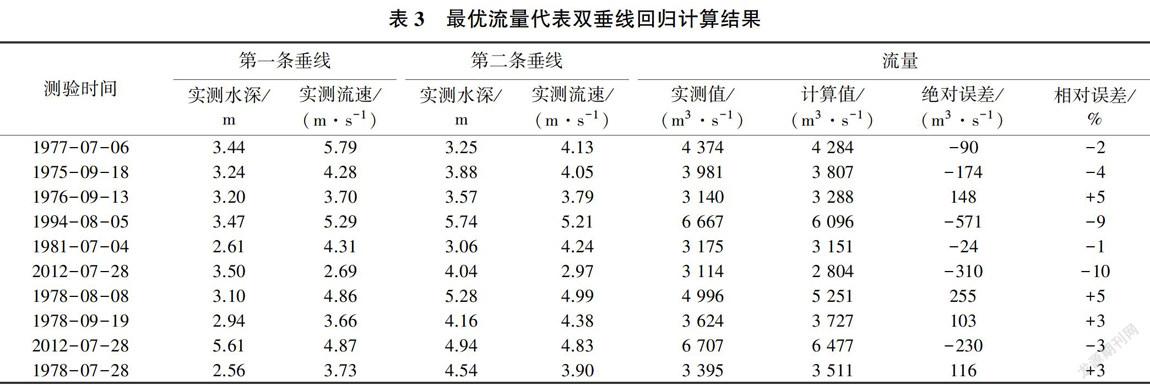
表3为在应用该最优解得到的回归计算结果中随机抽取10个测次的计算结果。
3 结语
(1)对于水深、流速、流量,使用两条代表垂线的实测值,均可以较为准确地回归计算相应的全断面综合值。
(2)水深代表单垂线的分析结果说明,单一垂线误差较大,且由于位置出现在断面中部,通常靠近中泓,因此不宜采用。
(3)从均方根误差来看,代表垂线法仍有改进余地。增加垂线数量和输人参数类别(如水位、河宽、预测流量级等)是两种主要的改进途径。
参考文献:
[1] 中华人民共和国水利部,河流流量测验规范:CB 50179-2015[S].北京:中国计划出版社,2015:84-101.
[2] 王锦生,水文测验手册[M].北京:水利出版社,1980:228-237.
[3] 董礼玮,陈河水文站代表垂线平均流速与断面平均流速关系分析[J].陕西水利,2015,33(2):186-188.
[4]张家军,拓自亮,郭德成,受水库调节影响的代表垂线法测流应用研究[C]∥第十二届中国科学技术协会年会论文集:第二卷,北京:中国科学技术协会,2010:1-6.
[5] 钱学伟,刘少华,声学多普勒测流原理及其应用[M].郑州:黄河水利出版社,2003:56-78.
【责任编辑翟戌亮】

