近视用户眼动数据校正
栗战恒 郑秀娟 刘凯




摘 要:近视会导致用户眼球发生形状畸变,近视用户眼球与视线估计中眼球参考模型的差异导致基于固定模型法得到的视线位置与用户实际视线位置不一致,这影响了视线跟踪的数据精度。针对以上问题,文中提出了一种基于眼球误差模型的眼动数据校正方法。结合眼动仪使用中例行的视线标定,通过计算视线标定过程中参考点与对应的视线估计点之间关系求得近视用户眼球与视线跟踪中眼球参考模型之间的眼球误差,然后根据眼球误差计算跟踪数据误差,最后将误差量补偿于眼动数据,并进行了计算机仿真验证。实验结果表明:近视用户眼球发生形状畸变时其眼动数据偏差不仅与近视程度有关而且与用户观察点位置密切相关。数据校正前,视线估计点与真实值平均偏离误差为48.66pixels;数据校正后,视线估计点均匀分布在真实值周围,平均跟踪误差为28.02pixels,并且可以验证,随着观察对象位置不同及近视程度变化,矫正后的数据偏差始终小于48pixels。说明以上提出的方法可以很好校正近视造成的眼动数据偏差。
关键词:眼动仪;视线跟踪; 校正;近视;眼动数据
中图分类号:TP 391 文献标识码:A 文章编号:1672-7312(2019)04-0512-05
0 引 言
在过去的20年间,关于视线跟踪的研究取得了很大的进步[1-2],但是由于人类眼部形状各异,而且其大小、闭合、位置和光源等条件的差异,使得视线跟踪技术仍旧面临一些难题。视线估计技术有基于模型和基于回归的2种类型。但是,大多数基于模型的视线估计方法常需要一些先验参数,如依据Le Grand眼球模型建立的单摄像机单光源系统使用了角膜半径经验值C=7.7 mm,人机交互层面广泛使用的Morimoto二次回归模型[3]建立在Gullstrand眼球模型之上,而后者需要角膜半径、折射率等先验参数值,Shao等提出的2D模型的视线估计方法除了使用先验的眼球半径外更是假定眼球光轴视轴重合[4]。
虽然大样本采样建模得到的眼球固定内参数具有普适性,但对于一些个体来说并不适用,视线估计中恒定固有内参数的使用可能会导致视线估计得到的眼动数据与真实数据不一致。针对以上问题,文中提出了利用原有眼动数据进行校正的解决方案,并进行了计算机仿真实验。
1 视线估计的影响因素
研究表明人的眼球在一定程度上与民族特征有关[5],并存在一定的个体差异。另外,近视造成的眼球畸变也会对基于模型的视线估计结果造成影响。近视被列为世界三大疾病之一,相关数据显示全球人口近视发生率为22%。近视者眼球形状的变化(尤其是高度近视者)使得依据先验的眼球模型得到的眼动数据不再适用。
近年来国内外一些学者开始致力于眼动数据校正方面的研究[6-13]。其中,Biele和Kobylinski[11]、Schenk等[8]采用了误差向量补偿法;Vadillo等[13]采用了拟合矩阵法;Zhang和Hornof [14]采用了线性回归向量法。上面提到的校正方法大多基于误差数据本身进行数据拟合,文中由导致眼动数据偏差的眼球误差模型出发,提出了利用原有眼动数据进行校正的解决方案,结合眼动仪使用中的视线标定,通过计算真实数据与误差数据之间关系求得眼球误差模型进而对眼动数据进行校正。
2 基于眼球模型的眼动数据校正
眼睛注视点的改变是靠眼球转动来完成的。为了简化计算,Shao等提出的模型拟合法将眼球视为围绕一固定点旋转的球体如图1所示,眼球中心与瞳孔中心的连线即为用户视线[15-16],文中根据此模型提出了眼动数据的校正方法。在眼动仪使用过程中,眼睛与屏幕位置关系如图2所示,其中O为眼球中心,Z为眼动仪,A为眼睛正视前方时视线与屏幕的交点。对于眼动仪系统,B点位置不变,A点坐标、OZ及OA距离可通过眼动仪数据采集获得,在以下讨论中A点坐标和OA值可视为已知量。
眼动仪在使用之前要先进行一个视线标定以匹配眼动视角与屏幕坐标之间的关系,然后进行相关操作,文中提出的眼动数据校正算法借助眼动系统的视线标定过程。眼动数据校正流程可简要概括为如下3个步骤:①由视线标定时屏幕参考点与对应的眼动视线估计点得到用户眼球与眼球参考模型间的眼球误差;②根据眼球误差计算跟踪数据误差;③将误差量补偿于眼动数据。视线标定时,参考点坐标已知,对应的视线估计点坐标可由眼动仪得到。由于双眼眼动数据的校正原理相同,文中以单个眼球为例进行校正原理分析。
2.1 近视用户的数据校正
研究表明,近视患者的眼球较正视者眼球更为狭长,随着近视屈光度数的增加,眼球前后径、垂直径和水平径均有增长[17-18],近视用户的眼球可以被假设为比正视者眼球大的球体模型。如图3所示,虚线圆为视线估计时的眼球参考模型,实线圆为近视用户眼球,两圆的共同圆心为O.A为眼睛正视前方时视线与屏幕的交点,OA垂直于屏幕平面。B为视线标定时的一个参考点,B1为用户注视B时基于模型的视线估计方法得到的视线估计点,A,B和B1在屏幕平面内共线。DE为用户从A看向B时瞳孔在水平方向的移动距离,FG为DE在眼球参考模型上的映射,DE=FG.基于模型的视线估计方法中视线由A点移到B1点对应眼球参考模型中瞳孔在水平方向上移动距离FG.
记OE/OG为ρ,即用户眼球与眼球参考模型半径之比。视线标定时,A点、B点、B1点坐标及OA距离已知,易求得AB,OB,OB1及AB1距离,进而可求得ρ。对于同一受试者,其ρ值固定不变。
视线标定完成后,用户视线点仍满足图3类似几何关系。重画图3,这里为方便表示用户实际视线点仍记作B,其他标注类似。进行视线估计时以上关系式仍然成立,可以推出
根据上式可以求得近视用户的实际注视点B的坐标。
2.2 视线校正的仿真验证
针对以上提出的校正方法采用计算机仿真进行验证。通常眼动仪的有效跟踪距离为50~80 cm,仿真时该距离设定為65 cm,并假设用户正视点(用户正视前方时,视线与屏幕的交点,对应上文中点A)位于屏幕中心,在宽高比为16∶9,屏幕分辨率为1 920×1 080 pixels的23.1英寸显示器上进行。视线跟踪过程中必然存在一定的眼球生理震颤和外界干扰从而造成数据误差,我们用实验拟合扰动误差模型,之后将其施加于计算机仿真来模拟实际情形。显示器屏幕被等分成9个部分,以每部分的中心作为测试参考点,并从上到下、从左到右依次编号为1,2,3,…,9.成年人眼球长度为23 mm左右,经典理论认为眼轴每延长1 mm,屈光力增加约3D[19].眼睛近视度数过高时易发生视网膜脱落,故仿真时选取近视度数范围为0°到1 380°,对应ρ的取值范围是1.0~1.2.
選取眼球半径比ρ为1.1,进行了10次仿真模拟实验。图4为近视用户校正前后视线误差对比图,图5为校正前后视线估计点对比图,测试点1~9表示屏幕上9个参考点。文中视线跟踪误差定义为参考点和所对应的视线估计点之间距离Δd的均值,单位为像素(pixel)。Δd越大,说明视线估计点位置和真实注视点位置之间的距离越远,估计点误差越大;反之,则估计点误差越小。
由图4及图5可知,校正前各参考点的视线估计点与屏幕中心的距离均大于真实值与屏幕中心的距离,视线估计点呈现四周发散的趋势。校正前,视线估计点与真实值偏离比较远;校正后,视线估计点均匀分布在真实值周围,平均跟踪误差为28.02 pixels(SD=3.34)。
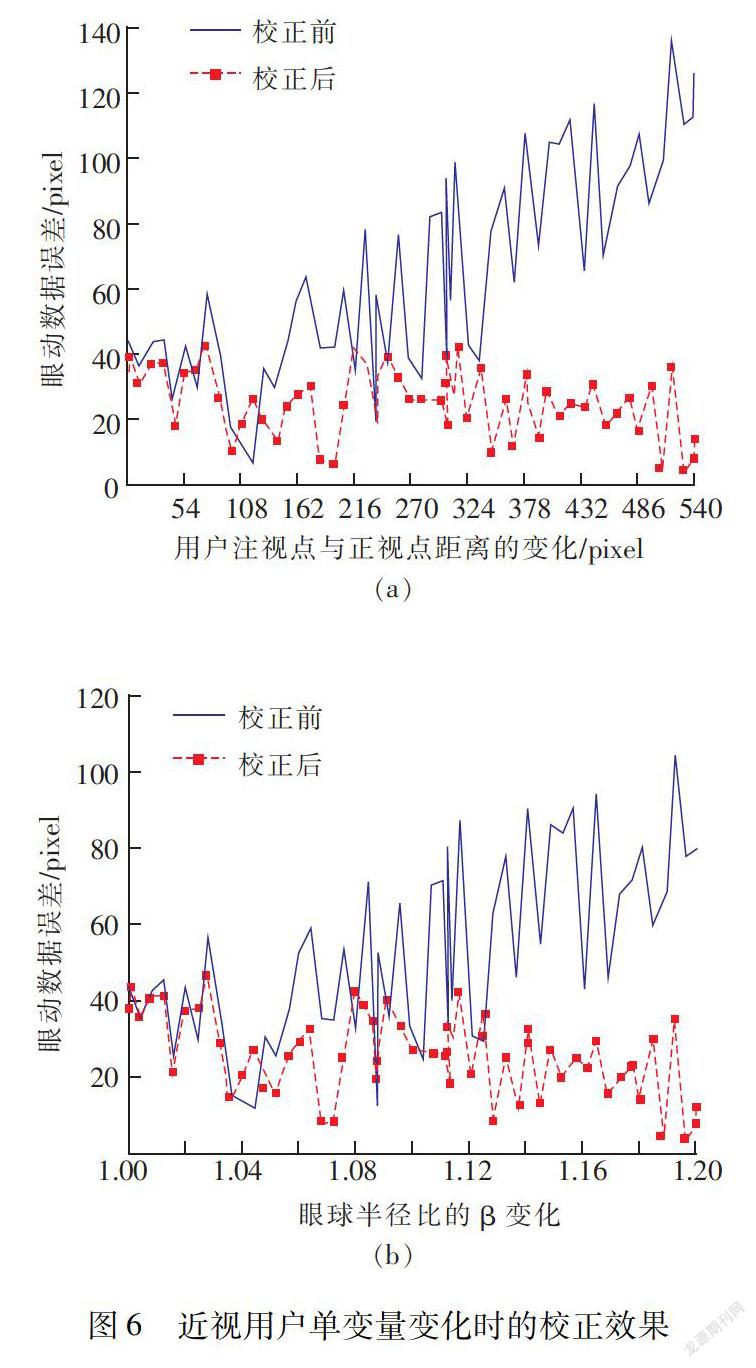
为了研究校正算法对单变量变化的校正效果,我们分别研究了用户注视点与正视点距离、近视程度单变量变化时的校正效果。图6(a)为选取ρ为1.1,当用户注视点与A点的距离由0变为540 pixels时的仿真图。显然,校正后数据偏差稳定在±44.18 pixels范围内,而校正前数据偏差随着注视点与正视点距离变大逐渐变大。图6(b)为用户注视点与正视点距离为384 pixels,ρ从1变化为1.2时的仿真图,随着近视程度的加深(即ρ从1变为1.2)校正前数据偏差越来越大,校正后数据偏差稳定在±47.29 pixels的范围内,并且可以验证校正后数据偏差小于48 pixels。以上仿真结果说明,用户近视时其眼动数据偏差不光与近视程度有关而且与用户注视点位置密切相关。
3 结 语
文中对由用户近视导致的特定情形下眼动数据不准问题提出了相应解决方案,仿真结果显示以上校正方法十分有效。可以校正近视导致的依据固定眼球模型得到的眼动数据不准,虽然针对基于模型的视线估计方法,但对于瞳孔—角膜向量法及其他算法同样具有参考作用(其他一些视线估计算法也在一定程度上借鉴了眼球生理模型)。文中校正算法对其他类型视线估计算法的适应性将在接下来进行研究。
文中仅列举了近视用户眼球误差模型并进行了公式推导和校正说明,其他类型的眼球误差模型校正原理相似。如,文中对近视者的校正中假设近视者眼球大于正视者的眼球,所以上述方法对用户眼球半径大于参考模型半径的情形同样适用。并且可以验证,当用户眼球半径小于参考模型半径时,上述校正算法同样成立。虽然文中提出的校正算法对近视导致的特定类型跟踪不准问题十分有效,但是存在一定的局限性,必须已知用户眼病类型才可对其进行校正。对于其他类型眼动数据的校正将在接下来进行讨论。
参考文献:
[1] 李晨辉,庞志兵,张艳君,等.眼动测量在人机界面作业优化评估系统中的应用[J].技术与创新管理,2017,38(01):41-45.
[2]郑秀娟,栗战恒,张 昀.基于视觉特性的驾驶安全眼动研究进展[J].技术与创新管理,2018,39(01):50-59.
[3]Morimoto C H,Koons D,Amir A,et al.Pupil detection and tracking using multiple light sources[J].Image & Vision Computing,2000,18(04):331-335.
[4]Shao G,Che M,Zhang B,et al.A novel simple 2D model of eye gaze estimation[C]//International Conference on Intelligent Human-Machine Systems and Cybernetics,2010:300-304.
[5]李作勇.关于近视[J].中国眼镜科技杂志,2000(06):30.
[6]Zhang Y,Hornof A J.Mode-of-disparities error correction of eye-tracking data[J].Behavior Research Methods,2011,43(03):834-842.
[7]Hornof A J,Halverson T.Cleaning up systematic error in eye-tracking data by using required fixation locations[J].Behavior Research Methods Instruments & Computers,2002,34(04):592.
[8]Schenk S,Dreiser M,Rigoll G,et al.GazeEverywhere:Enabling Gaze-only User Interaction on an Unmodified Desktop PC in Everyday Scenarios[C].CHI Conference,2017:3034-3044.
[9]Gibaldi A,Vanegas M,Bex P J,et al.Evaluation of the tobii eye X eye tracking controller and Matlab toolkit for research[J].Behavior Research Methods,2017,49(03):923-946.
[10]Zhang Y,Hornof A J.Easy post-hoc spatial recalibration of eye tracking data[C].Symposium on Eye Tracking Research and Applications,2014:95-98.
[11]Biele C,Kobylinski P.Surface recalibration as a new method improving gaze-based human-computer interaction[C].International Conference on Intelligent Human Systems Integration,2018:197-202.
[12]Binaee K,Diaz G,Pelz J,et al.Binocular eye tracking calibration during a virtual ball catching task using head mounted display[C].ACM Symposium on Applied Perception,2016:15-18.
[13]Vadillo M A,Street C N,Beesley T,et al.A simple algorithm for the offline recalibration of eye-tracking data through best-fitting linear transformation.[J].Behavior Research Methods,2015,47(04):1365-1376.
[14]Zhang Y,Hornof A J.Easy post-hoc spatial recalibration of eye tracking data[C].Symposium on Eye Tracking Research and Applications,2014:95-98.
[15]Kyung-Nam K,Ramakrishna R S.Vision-based eye-gaze tracking for human computer interface[C].IEEE International Conference on Systems.IEEE,1999(02):324-329.
[16]余 沁,劉龙繁,熊 艳,等.文字强调方式对多媒体学习的影响——基于眼动追踪技术[J].生物医学工程研究,2018,37(01):96-100.
[17]Atchison D A,Jones C E,Schmid K L,et al.Eye shape in emmetropia and myopia[J].Investigative Ophthalmology & Visual Science,2004,45(10):3380.
[18]Mutti D O,Sholtz R I,Friedman N E,et al.Peripheral refraction and ocular shape in children[J].Investigative Ophthalmology & Visual Science,2000,41(05):1022-1030.
[19]周跃华,李志辉.近视眼角膜屈光力及眼轴的测定分析[J].中华眼科杂志,1995(05):356-358.
(责任编辑:张 江)

