试议小学数学建模教学
夏兴旺
摘 要:模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。在小学数学教学中,教师应重视模型思想的渗透,通过有效的建模教学促进学生相关素养发展。本文以人教版五年级《植树问题》为例较为系统地探讨了小学数学建模教学的实施过程。
关键词:小学数学;模型思想;建模教学;植树问题
义务教育阶段数学课程表中中将模型思想列为核心素养要素之一,并指出:“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。在小学数学教学中,教师应重视模型思想的渗透,通过有效的建模教学促进学生相关素养发展。植树问题模型是小学高段最重要的模型之一,以下以此为例来简要探讨模型思想的在教学中的渗透,希望对一线教师有所助益。
一、化繁为简,便于操作探究
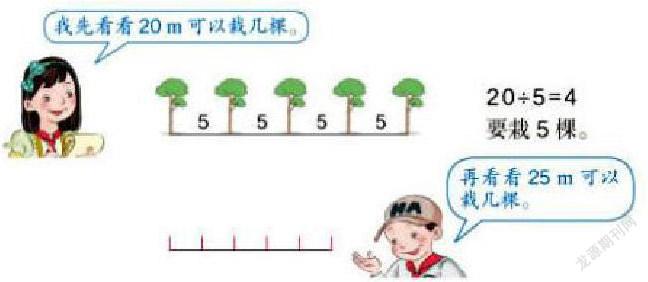
教材上首先以例题的形式给出一个实际问题情境,即“同学们在全长100m的小路一边植树,每隔5m栽一棵(两端要栽)。一共要栽多少树?”为了使学生获得良好的思维起点,进而循序渐进地掌握模型本质,可以化繁为简,以方便接下来的操作探究。实际上,即先让学生思考“在20米长的路边植树,每隔5米植一棵,一共需要多少棵树?”学生看到简化后的问题时,会相对较易得到正确答案,但一般并非是通过正式的建模并且找到其间的规律(即理解模型本质),事实上,从实际教学来看,不少学生由于受到习惯性思维的影响,看到题目后很会不假思索的想:全长÷间隔长度=棵数,所以一共需要20÷5=4棵樹苗,这个想当然的答案是错误的。这时就需要教师加以合理的引导点拨,按照教材上的思路,可以采取图形结合的方式帮助学生直观理解模型的本质。我们看下一环节。
二、图形结合,帮助直观理解
数学模型中包涵的规律往往是抽象的,对于以形象思维和具体思维占据主导的小学生而言,有着一定的理解上的难度,因此通过图形结合的方式将模型中包涵的规律直观呈现出来是最有效的途径之一。就植树问题而言,可以利用线段图来直观展示,使学生一目了然。如下图所示,学生可以发直观地看到分为4段的线段却有5个节点,即有4段间隔的小路需要栽5棵树:
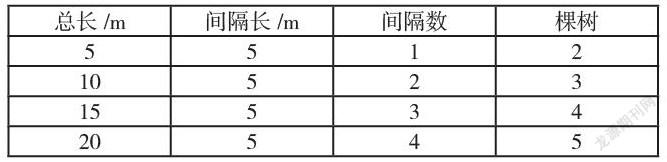
这时学生可以很容易的发现规律:20÷5=4,也就是总长÷间隔=间隔数,而种树棵树就等于间隔数+1=种树棵数,用25m来验证也是如此。这就是植树问题中包涵的数学规律,也即为数学模型的本质。值得一提的是,这个问题还可以引导学生采用列表法,从简单到复杂,找出一般性的规律,如下表所示:
上述两种方法,都可以算作图形结合,其好处就在于直观形象,便于学生发现规律,一般来说线段图最为常用,也最具效果,但列表法也自有特点,有助于学生发展和掌握规律,可以作为辅助性的一环。
三、观察对比,体会模型特征
在总结出数学规律,接下来即是通过观察对比,让学生体会模型的特征从而切实掌握模型本质。这里所说的观察对比,主要是指根据变异学习理论,呈现模型的变式,即两端都种、只种一端和两端都不种三种情况(教材上分别以例2和做一做中的第2题来呈现另外两种情况,可将其作为习题用于加深和巩固学生的理解)。让学生自己画出三种情况下的线段图(及表格图),并得出答案,发现规律,在观察和比较中掌握植树问题的数学模型。上一环节中所讨论的是两端都种的情况,有此基础,学生通过自主探究掌握其他两种情况是不难的。但在这一环节,教师要注重引导学生积极地展开思维活动,最终触摸到并把握住问题的本质。以下是这一环节的课堂实录片段:
师:“为什么都是在长20米的路的一边种树,每隔5米种一棵,却会有三种不同的情况呢?它们有什么相同的地方?”
生:“都是4段。”
师:“对,也可说是4个间隔。可以列出个算式吗?”
生:“20÷5=4(段)”
师:“好,20里面有4个5,在这个基础上想,为什么三种方案的植树棵树却不一样?棵树和段数有什么关系?”
生:“当两端都种树时,棵树等于段数+1。当只有一端种时,一段对应1棵树。当两端都不种时,棵树等于段数减1。”
至此,可以基本上全面彰示了植树问题的普遍性规律和模型特征。接下来则趁热打铁,进行适当的巩固拓展,力求达到使学生灵活运用数学模型的目的。
综上,本文以人教版五年级《植树问题》为例较为系统地探讨了小学数学建模教学的实施过程。事实上,小学数学建模教学当然是一个兼具深度和广度的课题,需要一线教师结合教学实践不断积极探索和总结,本文一己之见,尚盼同仁指教。
参考文献:
[1]德吉. 解析小学数学植树问题[J]. 西藏教育, 2016(9):30-31.
[2]刘丽秋. 小学数学建模教学的实践研究 ——以"植树问题"教学为例[J]. 考试周刊, 2017(66):115-115.
[3]代金凤. 构建模型提升能力发散思维——例谈小学数学中的“植树问题”[J]. 呼伦贝尔学院学报, 2012(3):110-112.

