基于“预习型导学案”预习模式的教学设计

杨静

【摘要】  建构主义认为，知识不单是由外到内的传递，而是学习者主动建构知识的过程，学习者获得是经验，而不是记忆事实和真理。本节课，我将学生的学习环节分为两部分——预习和课堂学习。课前提前布置了预习的任务，学习成绩优异的学生可以通过自学达到预习的目的，但是大部分的学生在自学时会遇到很多困惑，比如，在教材思考中，探索“五种两圆位置关系中，圆心距、两圆半径满足怎样的数量关系”，说明的不够清晰，有很多学生找不到解决的方法，因此我运用“预习导学案”，细化探索的过程，给学生提供自主探索的时间和空间，引导学生进行有效的预习。

【关键词】  数学 教学设计

【中图分类号】  G633.6                       【文献标识码】  A 【文章编号】  1992-7711（2019）06-256-02

《数学课程标准》指出：教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。为了培养学生的数学素养、增进学习数学兴趣，本节课在“预习导学案”上，我特意设置了一些活动，比如学生分小组制作“圆和圆的位置关系”的手工动画，学生绘制“生活中反映圆和圆位置关系”的实例。课堂专门设置展示环节，鼓励学生们到讲台进行展示。学生不仅锻炼了动手能力、合作意识，而且通过表达，深化了对问题的理解，将表层的认识内化。教师在学生探索的迷茫困惑处进行点拨，恰当使用多媒体辅助教学手段，帮助学生更好地认识和理解两圆位置关系的相关知识，解决教学中的难点问题，使学生真正完成知识感知、形成和巩固的过程。

整个教学过程体现如下特点：（1）借助预习导学案引导学生有效预习，培养学生自主学习的意识和习惯;（2）发挥学生的主动性，鼓励学生参与到教学中;（3）合理运用先进的教学手段，帮助学生解决问题，突破教学的难点;（4）注重学生的个体差异，设计不同层次的习题进行练习，保障每个层次的学生都学有所获，增强学生的学习欲望与学习热情，树立进一步学习的信心。

由于《课表（2011年版）》没有将“圆和圆的位置关系”列入目标要求，因此教科书将这一部分内容作为选学内容，安排在“实验与探究”。选择怎样的教学理念构建《圆与圆的位置关系》这一节课？课堂教学如何提升学生的学习效率？笔者带着这样的思考，结合目前研究的课题，选择以“预习型导学案”的数学预习模式为突破口，以提升课堂学习效率为主线，进行设计，现成文如下：

一、教学目标

知识与技能：掌握圆与圆的五种位置关系的定义、性质和判定方法;观察与现实生活有关的图片，丰富对现实空间圆的认识，建立初步的空间观念，发展形象思维。

过程与方法：学生按照“预习导学案”课前自学，经历思考和探索，带着问题听课，再次经历探究圆与圆的位置关系的过程，培养学生用运动变化的观点来分析和发现问题的能力;能用观察、实验、归纳、分类、概括、猜想、验证等数学方法，得出圆和圆的五种位置关系的性质和判定。

情感与态度与价值观：学生先学，教师再教，提升学习的自信心，体验成功的喜悦。学生在探究过程体会到学习的快乐，满足对数学的好奇心与求知欲。

二、教学重难点

重点：两圆的五种位置中两圆半径、圆心距的数量之间的关系。

难点：如何得出两圆的五种位置中（尤其是两圆相交时）两圆半径、圆心距的数量关系。如何把观察到的现象变成数学的表达是关键，也是今后应用的核心。

三、教学方法与手段

教法：体验学习教学法、引导探究发现法。

学法：自主学习，合作学习，探究学习相结合。

教学手段：预习型导学案、分层习题卷、学生手工制作的动画、ppt课件、投影。

四、教学过程

预习（预习型导学案）→课堂学习→课后作业

预习导学案

1.阅读24.2.3 圆和圆的位置关系（课本98-101页）

设计意图学生通过阅读，了解要学习的内容，体会问题的由来、研究方法和过程。有助于养成良好的阅读习惯.

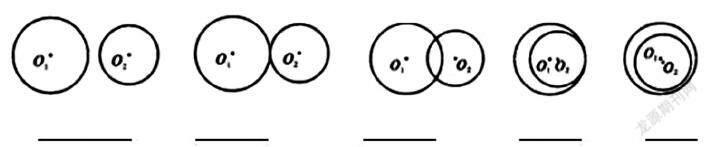
2.请说明下列圆与圆的位置关系

3.日常生活中圆和圆的位置关系的合理布局，为美丽的世界增添亮丽的色彩，请大家说出下列图中圆与圆的位置关系。

你能画出一个生活中圆与圆的位置关系的图案吗？

4.探究

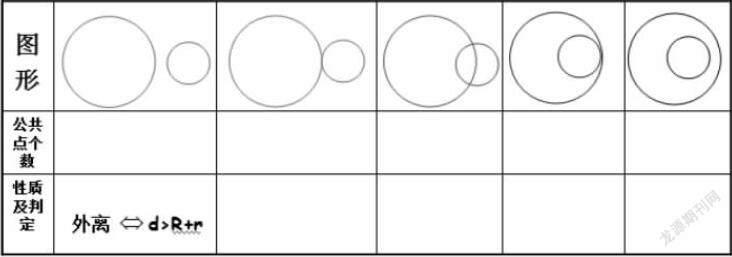
在五种位置关系中，两圆的圆心距d（两个圆心之间的距离）与两圆的半径R、r（R>r）间有什么关系？

思考： 如果已知两个圆的半径（r、R），圆心距（d），否可以判断出两圆的位置关系？试说明理由。

完成下列表格

5.课前练习

⑴若两圆没有公共点，则两圆的位置关系为（   ）

A .外离 B .内含    C .相切      D .外离或内含

⑵⊙O1的半径4，⊙O2的半径为2，两圆的圆心距为1，则两圆的位置关系是（）A内含 B 内切 C 相交 D 外切

⑶已知⊙O1和⊙O2的半径分别为3厘米和4厘米，若圆心距分别满足以下条件，分别判断⊙O1和⊙O2的位置关系。

O1O2=8cmO1O2=7cmO1O2=5cmO1O2=1cmO1O2=0.5cmO1和O2重合

6、制作一個手工，说明圆和圆的位置关系.分组制作一个即可，课堂到讲台展示

设计意图学生分组制作手工进行演示，不仅锻炼了动手能力、合作意识，而且通过表达，深化了对问题的理解，将表层的认识内化。

课堂教学过程

1.展示学生预习作业中部分优秀“预习导学案”。

设计意图展示优秀“预习导学案”，给学生提供展示、相互学习的机会，增强预习的效果。

2.探究新知，突破难点。

圆与圆的位置关系有几种呢？

生活中有很多反映圆和圆的位置关系的实例，你能再举出一些例子吗？

请学生到讲台展示他们的绘画作品。

那么在这些圆和圆的位置中，两圆的半径、圆心距之间满足怎样的数量关系呢？

你能用自己做的手工进行说明吗？请一个小组到讲台进行展示。

设计意图培养学生的合作意识、表达能力。

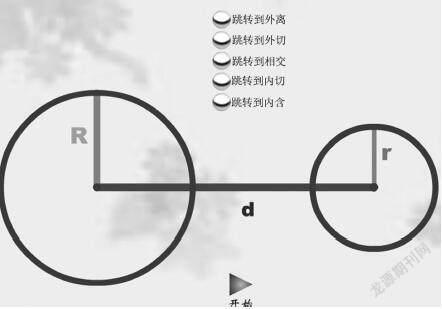
教师展示ppt动画。

小结

设计意图学生到讲台展示他们的绘画作品，培养学生表达能力，提升自信心.

课件展示“数量关系”，形象，突破本节课的难点，增强后进生对问题的理解. 课堂小结，帮助学生梳理，增强学生归纳的意识，通过提问后进生，检测学生情况

快速练习 在⊙O1和⊙O2中，半径分别为3厘米和4厘米，若O1O2 满足以下条件，请说明两圆的位置关系。

（1） O1O2=8厘米 （2）O1O2=7厘米（3）O1O2=5厘米

（4）O1O2=1厘米 （5）O1O2=0.5厘米 （6）O1和O2重合

你有簡便方法分享吗？（请2个学生到讲台展示简便方法）

3.例题讲解

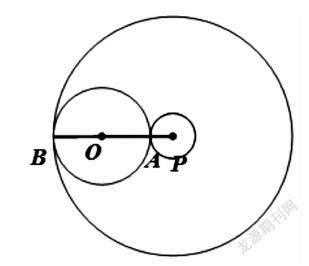
例题 如图⊙O的半径为5cm，点P是⊙O外一点，OP=8cm

（1）以P为圆心做一个圆与⊙O外切，这个圆的半径是多少？（2）以P为圆心做一个圆与⊙O内切呢？

设计意图选自教材中的例题. 内切和外切是圆和圆的位置关系中特殊的两个位置，此题重在强调这两个位置关系的特点，增进学生的理解。

4.分层练习

基础练习

⑴⊙的半径为4，⊙的半径为2，O1O2=1，则两圆的位置关系是（  ）

A 内含 B 内切 C 相交 D 外切

⑵两圆内切圆心距等于2cm，一个圆的半径等于6cm，

则另一个圆半径是（    ）

A 10cm B 4cm C 8cm D 4cm或8cm

⑶⊙O1 、⊙O2的半径分别为7和4，圆心距为d，若⊙O1 与⊙O2相交，则d取值范围是

⑷⊙O1 与⊙O2的圆心O1、O2的坐标分别是O1（3，0）、

O2（0，4），两圆的半径分别是R=8，r=2，则⊙O1 与⊙O2的位置关系是

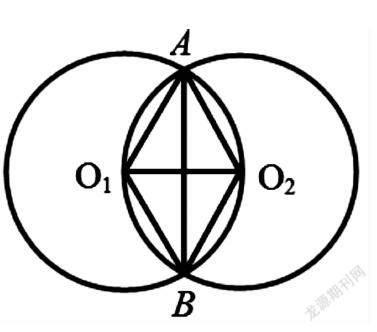
⑸如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心O2，求∠O1AB的度数。

⑹如图，在以点O为圆心的两个同心圆中，AB经过圆心

O，且与小圆相交于点A，与大圆相交于点B。小圆的

切线AC与大圆相交于点D，且CO平分∠ACB.

⑴ 试判断BC所在直线与小圆的位置关系，并说明理由;

⑵ 试判断线段AC、AD、BC之间的数量关系，并说明理由;

⑶ 若AD=8cm，BC=10cm，求大圆和小圆围成的圆环的面积。

设计意图 练习分为“基础练习”和“能力提高”，注重分层，课堂落实培优补差. 基础练习重在检测学生对知识点、基础题型的掌握情况. 有选择、填空、解答，题型多样. 能力提高题选择了1道，此题涉及直线与圆的位置关系，三角形的全等，猜想等等，综合性比较强。有助于学生思维能力的拓展，培养学生的综合运用能力和思维能力。

6.课后作业

A组（数学学习成绩优秀的）学习与评价74页达标训练1-7题、拓展训练1-7题;

B组（学习成绩中等的）学习与评价74页达标训练1-7题、拓展训练第7题;

C组（学困生） 学习与评价74页达标训练1-7题。

设计意图作业注重分层，落实培优补差.

本文系广州市教育科学“十二五”规划2016年度能效专项课题——以“预习型导学案”提升初中生数学学习效率的策略研究（编号1201574046）研究成果之一。