动感“轴对称”教学片段的设计与反思

唐剑岚 徐海曼

【摘 要】“轴对称”是图形与几何的重要基础内容，是发展学生抽象概括能力、直观感知能力、空间观念的重要素材。其中，掌握轴对称图形的特征和寻找图形的对称轴是教学难点。传统教学往往只注重对轴对称的概念进行辨析而淡化了学生对轴对称图形的动感理解，这是导致学生难以理解重点、突破难点的主要原因。文章试图基于“鱼渔欲”三位一体的教学理念，将Hawgent皓骏动态数学技术深度融入本节课，以期为提高小学数学的轴对称教学提供一定的参考。

【关键词】轴对称;动态数学技术;动感;小学数学

“轴对称”是北师大版三年级下册第二单元“图形的运动”内容，是图形与几何的重要基础内容，是发展学生抽象概括能力、直观感知能力、空间观念的重要素材。其中，掌握轴对称图形的特征和寻找图形的对称轴是教学难点。传统教学常常通过让学生看一看静态的轴对称图形，感知轴对称图形的概念。但由于模型本身的静态化与不可变化的局限，学生难以从模型中抽象出轴对称图形的概念。本文试图基于“鱼渔欲”三位一体的教学理念，将Hawgent皓骏动态数学技术深度融入本节课，尝试进行创课设计，以期为提高小学数学的轴对称教学提供一定的参考。

针对传统教学中图形动态化的不足，本文基于“鱼渔欲”三位一体的教学理念设计创课，达到了“授人以鱼”的同时实现“授人以渔”和“授人以欲”[1]41-46。首先，动感呈现轴对称的生活情境，让学生观察轴对称图形的特点;其次，动感呈现轴对称图形的问题情境;最后，设计轴对称图形的活动，让学生通过小组合作、交流获得长方形、正方形和圆的对称轴并分享，同时教师利用动态数学技术动感呈現它们的对称轴。根据上述的创课思路，研究者进行了“轴对称”概念教学片段的创课实录。1.看一看，说一说

师：今天我们要学习一种比较特殊的图形。大家先来看一看，它们有什么特点？

师：这是一只蝴蝶模型。在飞行过程中，两只翅膀好像（展示动画）……

生（齐声）：两只翅膀对折重合了！

师：大家说得真好！我们可以用数学的语言描述这些图形的特点吗？如果沿某条直线对折，对折的两部分完全重合，那么这样的图形称为轴对称图形，这条直线称为对称轴。可以简单记为“对折后能完全重合的图形是轴对称图形”。（动态呈现对称图重合过程及其对称轴，凸显概念的关键词和特点，如图1所示）

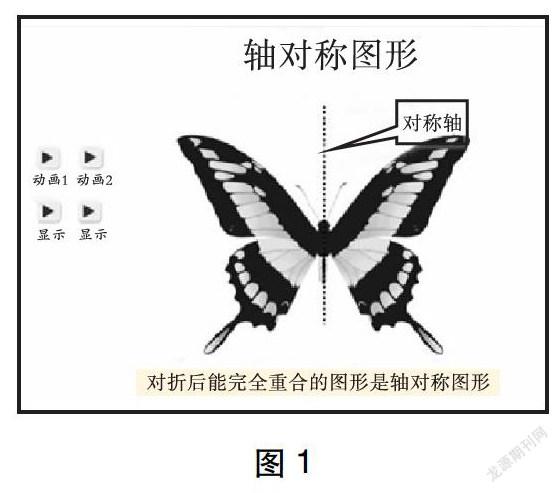
2.想一想，辨一辨

师：我们再来辨一辨，下面哪些是轴对称图形？（展示“囍”、两个三角板、长方形作业本）

师：婚礼中常见的“囍”是轴对称图形吗？

生（齐声）：是的！

师：你们是怎么知道的？

生1：沿中间那条直线对折，“囍”的两部分能完全重合。

师：不错！沿中间这条直线对折，“囍”的两部分完全重合，所以是轴对称图形，这条直线叫做对称轴。（动态呈现“囍”的对折过程和对称轴）

师：那这两个三角板（呈现实际的三角板）是轴对称图形吗？

生2：有两边相等的三角板是轴对称图形。

师：很好！（动感演示等腰三角板的对称轴，突出其轴对称的特点和关键性要素）3.折一折，展一展

师：现在请小组合作（事先给每个小组一组长方形、正方形和圆形的纸片），先折一折数学课本里面的轴对称图形，并说说这些图形有多少条对称轴;然后小组代表（小方代表长方形组，小镜代表正方形组，小圆代表圆形组）向全班进行展示、分享。

小方：长方形有2条对称轴。

师：不错。（动感演示长方形的对折过程和对称轴）

小镜：正方形有4条对称轴。

师：很好。（动感演示正方形的对折过程和对称轴，特别演示和强调对称轴是对角线的情况）

小圆（有点沮丧）：圆有很多条对称轴，但我们不知道一共有多少条。

师：很好的发现！其实圆是所有平面图形中最美的图形，因为它不论怎么看都是一样的图形，而且有无数条对称轴。（动感演示圆的对折过程和对称轴，特别演示和强调不管圆的位置和大小如何变化，圆依旧是轴对称图形，凸显圆的对称美，如图2所示）

根据基于“鱼渔欲”三位一体的教学理念[2]，本片段的三个环节突出了Hawgent皓骏动态数学技术融入数学教学的作用，在突出重点、破解难点的同时增强了学生学习数学的兴趣，达到了“授人以鱼”的同时实现“授人以渔与欲”，提升了教学的有效性。在“看一看，说一说”环节，首先创设贴近学生生活的问题情境——蝴蝶飞行，激活学生原有的知识与经验，找到旧知识生成新知识的生长点，激发学生的求知欲望[1]41-46;其次通过Hawgent皓骏积件动态呈现两只翅膀大小一样的蝴蝶的飞行过程，吸引学生的注意力，丰富学生的直观感知;最后促使学生表达，主动构建轴对称图形的特点。

在“想一想，辨一辨”环节，首先帮助学生理解轴对称图形的概念;其次设计变式的问题情境，加强学生对轴对称图形的概念辨析;最后通过Hawgent皓骏积件数形结合动感展示轴对称图形的疑难点、模糊点和关键点，提高学生学习数学的兴趣。

在“折一折，展一展”环节，首先，提供合作交流的平台，通过小组合作找出长方形、正方形和圆的对称轴，营造民主、宽松、和谐的学习氛围，激发学生学习的积极性和主动性;其次，丰富学生动手实践、交流展示等基本活动的体验，

发展抽象概括能力、空间观念等素养[3];最后，动感数形结合呈现长方形、正方形和圆对折的过程，在帮助学生破解难点的同时，引出平面图形中圆最美在于对称美，再一次展示了有情、有味、有趣的动感数学，突出了技术深度融入数学，实现“授人以鱼”的同时又实现“授人以渔与欲”，提升数学教学的有效性。

当然，如上教学过程并非一成不变，教师应根据学情，调整或改变活动的顺序。如果学生在“辨一辨”环节不能很好地辨析轴对称图形，那么教师可以先呈现对称的动画过程，然后再小结;如果学生不能很好地进行“折一折”活动，那么教师可以先示范，再组织学生合作探究;如果学生在“展一展”环节不能很好地展示成果，那么教师可以动态呈现轴对称图形的对折过程并加以补充，直到大多数学生能够理解寻找对称轴的方法。

参考文献：

[1]唐剑岚，周元.“授人以鱼”的同时“授人以渔与欲”：以《等差数列的前n项和》公式推导片段为例[J].数学通报，2016（9）：41-46.

[2]唐剑岚，陈圆.基于“鱼渔欲”三位一体优化教学理念的数学创课设计：以“一次函数的图象与性质”的教学为例[J].中小学课堂教学研究，2017（12）：34-37.

[3]吕小平，曹志忠.“轴对称”教学实录与评析[J].小学数学教育，2018（7）：127-129.