高中数学教学中图示理论的应用

刘文国

摘 要：高中数学较为复杂、抽象，这困扰了不少学生的学习。在教学过程中，一些教师主要采用灌输式教学法，这导致学生不能够很好地理解知识。如果教师将图示理论应用到教学之中，就能够理顺学生的思维，加深学生对知识的理解。本文主要围绕图示理论在高中数学教学中的应用进行分析。

关键词：高中数学;图示理论;应用

前言：在高中数学教学中，如果教师将图示理论应用到其中，那么就会发现理论学习与实践之间有着较强的关联性。在数学理论知识上，图示理论能够帮助学生去理解相关的知识点，在定理的理解以及概念的把握上，能够发挥重要的作用。基于此，围绕高中数学教学中的图示理论应用进行分析具有重要的意义。

一、图示理论的概念阐述

图示这个概念的发展较为悠久，许多人认为，图示就是在脑海中已经形成的固有知识结构，还有一些人认为，图示是固有的认知结构，这与上文所述的知识结构有所差异。此外，还有一些人表示不同的看法，他们认为图示并非知识结构，而是对经验的组合。尽管这些理解有所不同，但是也有一定的相似之处，那就是图示可以看作是脑海中具备的知识或者经验的组合。

在对图示的探索中，心理学家皮亚杰就进行了深入的探究，因此许多人都就将皮亚杰理论看作是图示理论。在该理论中，学习的发生主要是以图示为基础的，在学习过程中，主要由顺应、图示、同化以及平衡等几个部分所组成。

在以往的教学过程中，教师在数学理论方面的讲述主要采用灌输式教学法，这种教学方法不利于学生对知识的理解。而随着新课改的改革实施，许多教师逐渐将图示理论应用到教学之中，以帮助学生更好的理解知识[1]。

二、在高中数学教学中，图示理论的应用分析

2.1发挥学生的已有图示

在教学过程中，图示理论的应用较为广泛，如，在学习数学概念之时，学生在理解该概念的过程中，能够凭借原先的经验去进行理解。如，在学习“圆锥曲线”的知识时，教师就需要先给学生讲述圆锥曲线的由来：也就是用一个平面用不同的方式去截一个圆锥，这样一来，就可以得到不同的曲线，从而产生橢圆、双曲线等概念。而在教学中教师可以发现，尽管在学生在生活中会对这些概念有所了解，但是在学习数学知识的时候，这些图示并不能够促进学生的学习。因为双曲线、抛物线以及椭圆的形成，需要通过两个定点的关系来进行定义，或者通过一个点以及一条直线之间的关系来进行定义，但是这种方法不利于学生的理解。如，对于抛物线的理解，大多数学生认为就是一个物体抛出去然后形成的轨迹，所以若是为学生呈现另一种抛物线的定义，如将其定义为一个定点和一条直线的距离相等的点的轨迹，那么学生就很难去理解这个知识概念。

在对图示理论进行应用时，可以分为以下几个步骤：

第一，教师可以先引导学生说出自己对椭圆的理论，以及对双曲线知识的理解。这样一来，就能够使图示变得更加的清晰。第二，教师对计算机技术进行利用，利用动画表现的方式来呈现平面与圆锥的相切[2]。

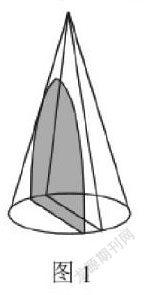
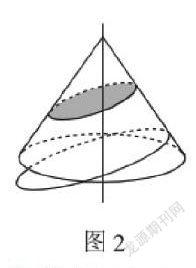
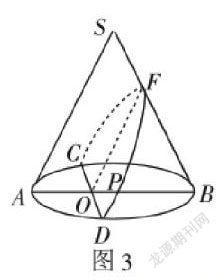
当截面位置与圆锥曲线平行时，那么所成截交线便是双曲线，如图1。而当截面的位置倾斜于圆锥轴线时，那么所形成的截交线便是椭圆，如图2。当截面的位置与圆锥的一条母线平行时，那么所形成的截交线便是抛物线，如图3。教师在演示之后，可以让学生去进行总结归纳。第三步，教师利用直线与定点之间的距离条件，对这几种概念进行重新讲解，对这两种认识的方式进行对比，并建立新的图示。

2.2引导学生利用图示解决实际问题

在教学过程中，教师不仅要让学生掌握教材中的理论知识内容，还需要培养学生分析问题以及解决问题的能力。因此，在应用图示理论时，教师需要引导学生将该理论应用到实际问题的解决之中。事实上，教材或者试卷中的许多习题都有着一定的生活背景，而这对于学生的图示理论的应用是一个较大的考验，那么在巩固复习的时候，教师可以多设计一些与生活有关的例题[3]。

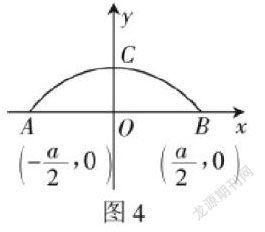
如，按照我国汽车制造的情况，一般卡车的宽为1.6米，高为3米。现在要设计横断面为抛物线型的双向二车道的公路隧道，为了确保车辆的行驶安全，交通管理部门作出了相应的规定，规定汽车在进入隧道之后，需要保持距中线0.4米的距离行驶。已知拱口AB宽刚好使拱高OC的4倍。若拱宽为a米，求能够使卡车安全通过时a的最小正整数值。

在解决本题时，可以归纳为以下两步，（1）根据实际问题的意义，引导学生找到解题的途径，得到距拱口中点2m处y的值。（2）然后将不等式y>3，再结合实际问题的值得到a的值。值得注意的是，在应用图示理论进行教学时，教师需要坚持过程性原则，也就是让学生自己去探究问题，思考问题中的已知条件与未知条件。或者是让学生相互讨论，去进行小组交流，让他们分享自己对知识的看法，这样才能够加深他们对知识的理解。所以在解决这道题时，教师应该先给予一定的时间让学生思考，然后再对题目进行讲述。

结语：综上，在高中数学教学中，图示理论能够加深学生对知识的理解，提高学生的数学学习水平。那么在今后的教学中，教师需要改变传统灌输式教学的做法，将图示理论应用到教学之中，鼓励学生发表自己的看法与观点。在应用图示理论教学时，教师要发挥学生的已有图示;并引导学生利用图示解决实际问题。这样一来，学生对图示理论的应用也会更加的熟练，他们对数学定理、概念等知识的理解也会更加的深刻，进而提升他们的数学学习能力。

参考文献

[1]赵钰.高中数学教学中图示理论的应用[J].中学数学，2019，03：82-83.

[2]常勇.图式理论在高中数学教学中的应用探究[J].数学教学通讯，2017，15：70-71.

[3]萨仁格日乐.基于图式理论的高中英语听力策略培训研究[D].内蒙古师范大学，2012.