从STEM教育视角看折纸

常文武

摘要：随着计算机辅助设计和互联网的发展，折纸这项古老的艺术也迅速现代化，被多学科的科学家、技术员、工程师所关注，形成了一个新的STEM门类，在跨学科教育领域焕发出新的生命力。通过鳖臑和爬坡陀螺两个案例，管窥折纸之于数学教育和科学教育的可能与价值，说明折纸不但是当之无愧的STEM教育优良载体，而且在投入产出比方面还优于已有的STEM教育项目。

关键词：折纸STEM教育鳖臑爬坡陀螺

简便易行的折纸活动通常仅被视为传统的手工游戏。但是，随着计算机辅助设计和互联网的发展，折纸这项古老的艺术也迅速现代化，被多学科的科学家、技术员、工程师所关注，形成了一个新的STEM门类，在跨学科教育领域焕发出新的生命力。

审视中国，STEM教育正在如火如荼地展开，各地创新实验室四处开花。但是，里面通常只能找到一些电子设备，如机器人编程和3D打印等——虽然上海市中福会主办的上海市青少年STEMx实践展示交流活动在5年前就将创意叠纸纳入为赛事项目之一。

环顾世界，折纸正在把它艺术的根系延伸到科学、技术、工程和数学等领域。芬兰的动手课上充满了用平凡的纸张制作的模型。以色列的小学生长期以来在用折纸学习几何学。美国MIT的工程师在给大学生开折纸算法课。折纸技术被用在太空望远镜镜片的折叠设计和人造血管支架的设计上。玩具设计师和时装设计师都在折纸中寻找创作的灵感……

下面，从数学和科学的角度提供两个案例，说明折纸不但是当之无愧的STEM教育优良载体，而且在投入产出比方面还优于已有的STEM教育项目。

一、折纸让数学更加亲和

传统观点认为（甚至统计数据也表明），数学是女生不太擅长的。但折纸往往是女生较为喜欢参与的活动。上海市第三女子中学的颜雯婕老师引领学生通过折纸学习立体几何。她们的实践表明，女生在折纸活动中找到了立体感，比以前更愿意尝试解决相关的数学问题。

下面，以笔者设计的一款折纸教具——鳖臑（这款教具于2016年获得教育部装备中心颁发的“优秀教具奖”，于2018年被纳入台湾高中数学课外读物《折纸学数学》中）为例，谈谈利用折纸教学立体几何的可能性与价值。

这款教具取名为鳖臑，是因为这个结构在《九章算术》里被称为鳖臑。《九章算术》“商功”章给出了堑堵、阳马和鳖臑的概念及体积计算公式。堑堵是底面为直角三角形的直棱柱，阳马是底面为长方形、一条棱垂直于底面的四棱锥，鳖臑是四个面均为直角三角形的三棱锥。若斜剖正方体，就得两堑堵;若斜剖堑堵，就得一阳马和一鳖臑。堑堵、阳马和鳖臑都可看作线面垂直的模型。2015年湖北高考数学卷就曾以此为背景命题。

不过，即使是专门研究数学史的华东师范大学汪晓勤教授，也认为鳖臑实物模型并不寻常。那么，怎么用折纸来实现这个稀罕物呢？以下便是具体的取材、折叠过程：

1.从一张A4纸出发，沿着长边剪去一条宽度为7 cm（短边长的13）的纸条，用剩余的23张纸完成折叠。

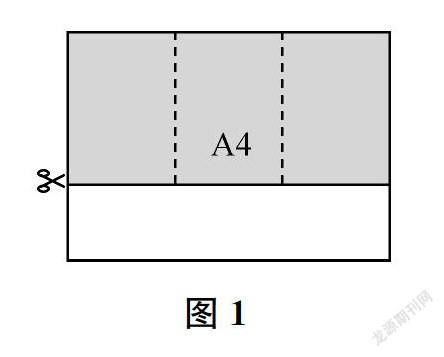
2.将剩余的纸条沿着长边三等分折叠（如图1）。

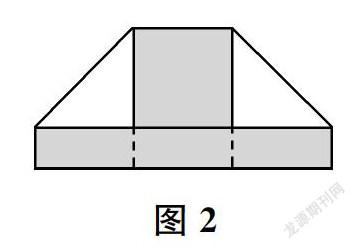
3.将左上及右上两个直角折向三等分线，得到一个“帐篷”（如图2）。

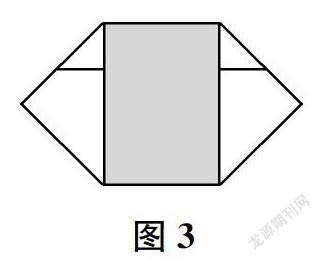
4.将左下角和右下角折向相应的三等分线，得到一个“纺锤”（如图3）。

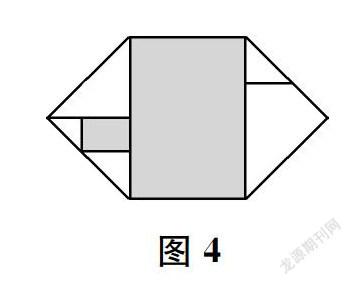
5.将左边顶层纸过顶点向下对折，使折痕恰为该直角的平分线（如图4）。

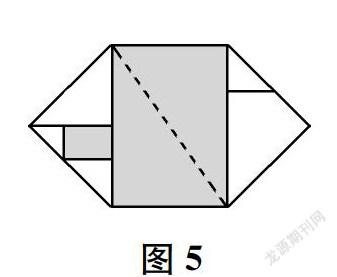
6.折出中心区域长方形的一条对角线（如图5）。

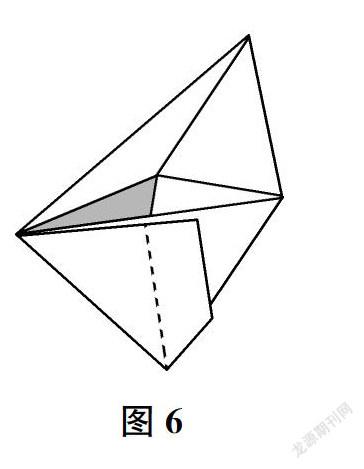
7.沿着第6步折出的对角线将左侧的纸折起，同时，拉出第5步折起的直角梯形，将其藏入右边大三角形的锐角处（如图6）。

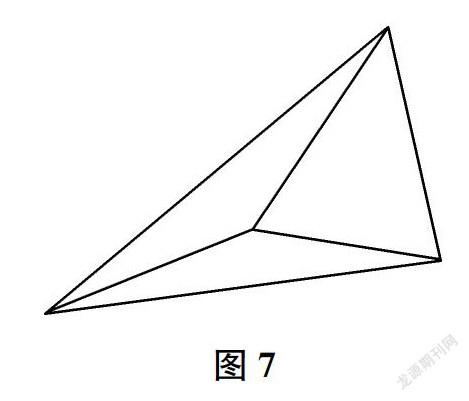
8.将第7步中散开部分上方的四边形前端伸入三角形洞口，整理平整作品（如图7）。

作品完成了，但真正的探索才刚刚开始。《九章算术》里还有两个不易理解的结论：“合两鳖臑成一阳马，合三阳马成一立方。”为了理解“合两鳖臑成一阳马”（这一句最难理解，因为学生对立体图形的“面对称”认识不深;后一句稍好理解，因为学生知道等底、等高的情况下柱体体积是锥体的3倍），我们要做一个镜像对称的另一种鳖臑：将上面第5步改为折出右边顶层直角的平分线，第6步改为折出中心区域长方形的另一条对角线;第7、8步相应做镜像对称。为了正确“拼合”两个鳖臑组成一个阳马，我们需要尝试将哪两个面做拼合面：可以发现，只有将两个非等腰的直角三角形面拼合，才能得到一个阳马。

通过以上实际制作和拼合的实践可见，对于这个数学史典籍中的立体模型的认识，动手是理解相关概念、内化相关知识的必由之路。汪晓勤教授HPM工作室的高振严老师和何伟淋老师曾经在他们合作开发的“线面垂直判定定理”课例中引入过鳖臑模型，而台湾凤山高中的连崇馨老师曾经借助于这个鳖臑教具开发出“三垂线定理”（线面垂直判定与性质的综合应用）的一个授课教程。

其实，从折纸活动本身中，学生也可以得到自我教育。经过多次失败，学生能够充分体会到“折叠精准方能拼合紧密”的道理，进而在不知不觉中形成做事要精益求精的價值观。

二、折纸让科学不再神秘

爬坡陀螺是一款有趣的体现物理原理的科普教具。将一个双头尖的锥体放在一个“V”形轨道低处的尖端上，它就会向着高处的开口端滚去。这个现象看似有悖于常识，但是恰恰符合了水往低处流的重心下降原理。

马来西亚资深科普教育家张宝幼女士曾编撰过一本科普书，收录了这款纸质魔术道具的制作方法。

然而，如果按照这本科普书的制作方法，就需要在锥面上用胶粘贴众多细小的脚。在曲面上用胶以及粘贴的部分太过细小，会导致不易粘牢，颇费周章。如果能够借鉴其他的纸模成型技术，用卡榫的方式连接，就可以变得更牢靠、更便捷和更有趣了。笔者实际操作后发现效果确实不错，在此简要叙述一下制作过程：

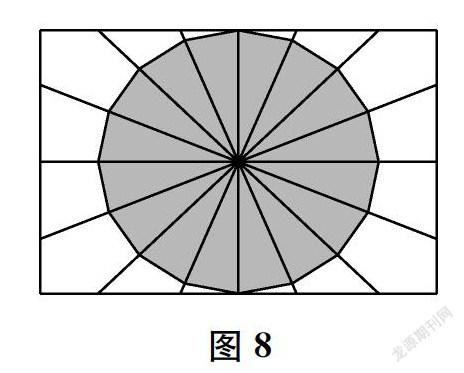
1.将一张较厚的A4纸（≥180克）两次对折，得到一个十字交叉的中心。继续对折每个90°角状区域，得到8个45°角状区域。如此细分下去，得到16个等分角状区域。将这些角状区域收拢压平，切出近似的圆形纸片（如图8，切痕为直线时实际为正16边形）。

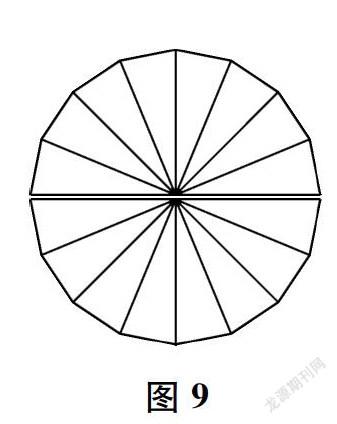
2.将得到的近似圆面沿一道折痕切分成两个半圆（如图9）。

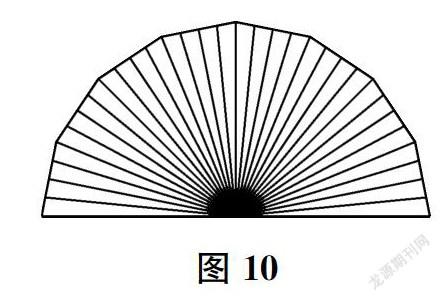
3.如果仅靠每个半圆的8个等分角状区域来制作圆锥（实际上是棱锥），那么它的滚动性不够好，所以还需要继续细分。通过不断的对折，将每个等腰三角形的顶角4等分（如图10，实际操作时可以将重点放在边缘部分的等分折叠上）。

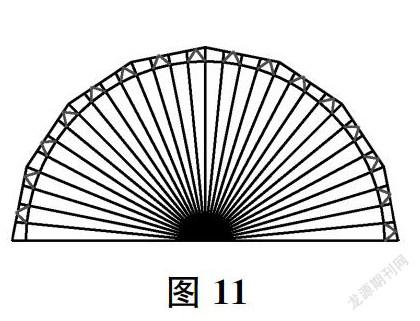
4.用圆规（或折叠的方法）在离边缘约1 cm的地方作一个同心的半圆。间隔地剪开16个“∧”形缺口（如图11），使得两个相邻缺口之间形成一个燕尾状的纽襻，从而产生随后两个圆锥互相卡扣的榫头。

5.将每个半圆两边黏合，使重叠部分正

好有一端的首个榫头覆盖另一端的首个榫头（π16弧度角）。将锥体的15个尖角内折，15个燕尾榫头外折（如图12）。

6.让两个锥体的接缝尽量处于接口圆的直径两端（保持重心位于几何中心），以尖角内折处为卯眼，将燕尾榫头置入。利用纸的柔韧性，只需将两个锥体相对且毗邻的榫头互换前后关系即可（如图13）。

在爬坡陀螺的制作过程中，学生可以体验到圆锥的展开以及卡榫结构类似拉链的功能和特性。

有了爬坡陀螺这款教具，便可设计教学活动，引导学生认识这种结构在“V”形轨道上的怪异行为。从中间打开一本杂志，将张开的角度调至约120°;将其立于一个斜面上，使書脊位于斜坡的低处，开口朝向斜坡的高处;将爬坡陀螺放在书脊处（如图14，这里利用了

椅子面的斜坡）。松手后，爬坡陀螺就会向开口处滚去。用一把直尺测量爬坡陀螺启动时的尖端高度以及滚落轨道时的尖端高度，二者之差一定是正值。

三、从STEM教育视角看折纸

STEM教育的精神就是依托跨学科探究，

实现多学科融合，培养创新意识和问题解决能力。在合理的难度设计下，各个年龄段的学生都可以在动手操作中体验到STEM教育的神奇魅力。

以上两例仅是大量体现STEM教育精神的折纸活动的典型代表。第一个案例主要体现了数学模型与工程结构的融合。该案例后续还有很多可探究的地方，如更一般的鳖臑如何折制。第二个案例则体现了科学原理与工程结构的融合。重心向下移动才能释放势能产生动能，通过测量和比较可以发现，运动体实际上是在向地心方向移动;拉链的结构用在纸模上，是问题解决和创新能力的体现。

最后，值得一提的是，STEM教育在美国很多是由公司运作的，他们向学校提供课程和师资培训。学校只需采购课程和派出教师接受培训。最终由公司派出的师资或学校的教师完成授课。这种模式充分调动了社会资源，达到了资源的合理配置。而中国目前采用的方式还只是采购一个创新实验室，在课程建设和师资培训方面没能建立起资源共享的机制。

参考文献：

[1] 高振严，何伟淋.“线面垂直判定定理”：从历史看证明、找模型[J].教育研究与评论（中学教育教学），2018（7）.